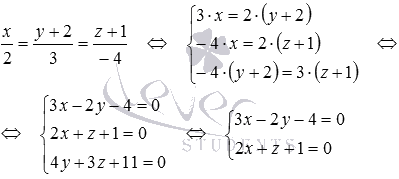Вы будете перенаправлены на Автор24
В основе способов построения параллельных прямых с помощью различных инструментов лежат признаки параллельности прямых.
- Построение параллельных прямых с помощью циркуля и линейки
- Готовые работы на аналогичную тему
- Построение параллельных прямых с помощью угольника и линейки
- Построение параллельной прямой, отстоящей на заданное расстояние от данной прямой
- Другие способы построения параллельных прямых
- Решаем задачи на построение — часть 3
- Уравнение прямой, проходящей через заданную точку параллельно заданной прямой.
- Уравнение прямой, проходящей через заданную точку плоскости параллельно заданной прямой.
- Уравнения прямой, проходящей через заданную точку пространства параллельно заданной прямой.
- 📺 Видео
Видео:Построение прямой, параллельной даннойСкачать

Построение параллельных прямых с помощью циркуля и линейки
Рассмотрим принцип построения параллельной прямой, проходящей через заданную точку, с помощью циркуля и линейки.
Пусть дана прямая и некоторая точка А, которая не принадлежит данной прямой.
Необходимо построить прямую, проходящую через заданную точку $А$ параллельно данной прямой.
На практике зачастую требуется построить две или более параллельных прямых без данной прямой и точки. В таком случае необходимо начертить прямую произвольно и отметить любую точку, которая не будет лежать на данной прямой.
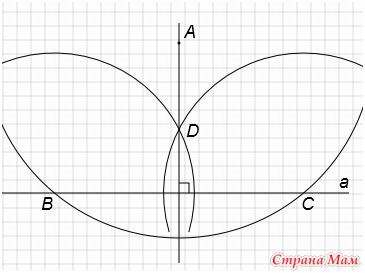
Рассмотрим этапы построения параллельной прямой:
- Выберем произвольную точку на данной прямой и назовем ее $В$. обратим внимание, что выбор точки абсолютно произвольный, т.к. не влияет на результат построения.
- С помощью циркуля и начертим окружность радиуса $АВ$ с центром в точке $В$.
На пересечении окружности и прямой отметим точку и назовем ее $С$.
С тем же радиусом $АВ$ построим окружность с центром в точке $С$. Обратим внимание, что вторая построенная окружность обязательно должна пройти через точку В при правильном выполнении построения.
С прежним радиусом $АВ$ построим третью окружность с центром в точке $А$.
Отметим точку пересечения второй и третьей построенных окружностей и назовем ее $D$. Отметим, что третья окружность при правильном построении также должна пройти через точку $В$.
Через точки $А$ и $D$ проведем прямую, которая будет параллельной заданной.
Таким образом, получили параллельные прямые $ВС$ и $АD$:
$BC parallel AD$, т. $A in AD$.
На практике также применяют метод построения параллельных прямых с помощью чертежного угольника и линейки.
Готовые работы на аналогичную тему
Видео:Построение прямой, параллельной даннойСкачать

Построение параллельных прямых с помощью угольника и линейки
Для построения прямой, которая будет проходить через точку М параллельно данной прямой а, необходимо:
- Угольник приложить к прямой $а$ диагональю (смотрите рисунок), а к его большему катету приложить линейку.
- Передвинуть угольник по линейке до тех пор, пока данная точка $М$ не окажется на диагонали угольника.
- Провести через точку $М$ искомую прямую $b$.
Мы получили прямую, проходящую через заданную точку $М$, параллельную данной прямой $а$:
$a parallel b$, т. $M in b$.
Параллельность прямых $а$ и $b$ видна из равности соответственных углов, которые отмечены на рисунке буквами $alpha$ и $beta$.
Видео:КАК ПОСТРОИТЬ ПАРАЛЛЕЛЬНУЮ ПРЯМУЮ ЧЕРЕЗ ЗАДАННУЮ ТОЧКУ? Примеры | МАТЕМАТИКА 6 классСкачать

Построение параллельной прямой, отстоящей на заданное расстояние от данной прямой
В случае необходимости построения прямой, параллельной заданной прямой и отстоящей от нее на заданном расстоянии можно воспользоваться линейкой и угольником.
Пусть дана прямая $MN$ и расстояние $а$.
- Отметим на заданной прямой $MN$ произвольную точку и назовем ее $В$.
- Через точку $В$ проведем прямую, перпендикулярную к прямой $MN$, и назовем ее $АВ$.
- На прямой $АВ$ от точки $В$ отложим отрезок $ВС=а$.
- С помощью угольника и линейки проведем прямую $CD$ через точку $С$, которая и будет параллельной заданной прямой $АВ$.
Если отложить на прямой $АВ$ от точки $В$ отрезок $ВС=а$ в другую сторону, то получим еще одну параллельную прямую к заданной, отстоящую от нее на заданное расстояние $а$.
Видео:Как построить прямую, перпендикулярную данной прямой через точку, которая лежит на данной прямойСкачать

Другие способы построения параллельных прямых
Еще одним способом построения параллельных прямых является построение с помощью рейсшины. Чаще всего данный способ используют в чертежной практике.
При выполнении столярных работ для разметки и построения параллельных прямых, используется специальный чертежный инструмент – малка – две деревянные планки, которые скрепляются шарниром.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 22 07 2022
Видео:Параллельные прямые циркулемСкачать

Решаем задачи на построение — часть 3
Продолжаем рассматривать элементарные геометрические построения.
5. Построить прямую, проходящую через данную точку и перпендикулярную данной прямой
Проведём окружность с центром в точке А таким радиусом, чтобы она пересекла прямую а в двух точках. Назовём их В и С.
С центром в точке В проведем окружность радиусом больше половины длины отрезка ВС.
C центром в точке С этим же радиусом проведём окружность. Получим точку D. 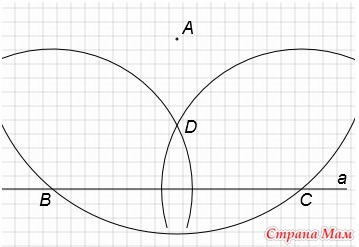
Через точки А и D проведём прямую. Она будет являться перпендикуляром к прямой а.
6. Построить прямую, проходящую через данную точку и параллельную данной прямой
Полагаем, что нам дана прямая а и точка К, не лежащая на прямой а.
Выбираем произвольную точку Т, не лежащую на прямой а и отличную от точки К. Проводим через точку Т перпендикуляр к прямой а (смотри элементарное построение №5), обозначим его прямой b. Через точку К проводим перпендикуляр к прямой b (смотри элементарное построение №5). Построенный перпендикуляр — прямая, параллельная данной прямой.
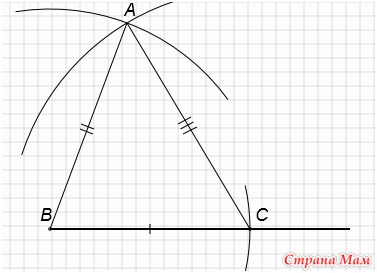
7. Построить треугольник по трем данным сторонам
Дано: отрезок а, отрезок в, отрезок с 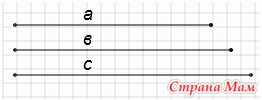
Построим произвольно луч.
Отложим на луче отрезок, равный отрезку а. Для этого сделаем раствор циркуля равным длине отрезка а и проведем окружность с центром в начале луча этим радиусом. Получим точки точки В и С. 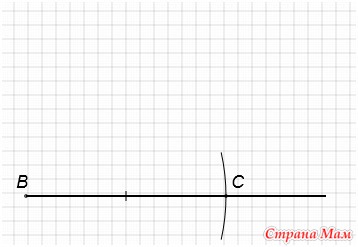
C центром в точке В проведем окружность радиусом равным длине отрезка в. 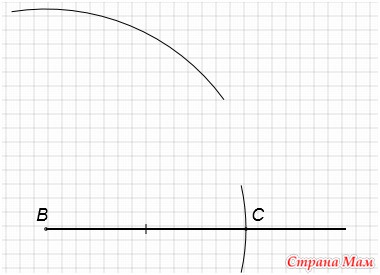
C центром в точке C проведем окружность радиусом равным длине отрезка c. Получим точку А. 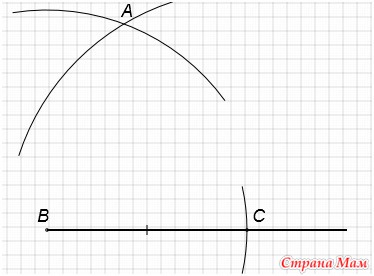
Соединим точку А с точками В и С. Получим треугольник АВС.
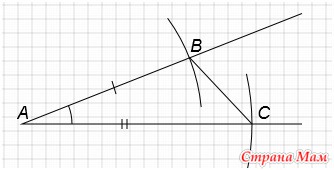
8. Построить треугольник по двум сторонам и углу между ними
Дано: отрезок а, отрезок b, угол A1 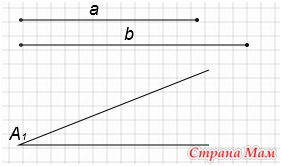
Построим угол А, равный углу А1 (Смотри элементарное построение №4).
С центром в точке А проведем окружность радиусом равным длине отрезка а. Получим точку В. 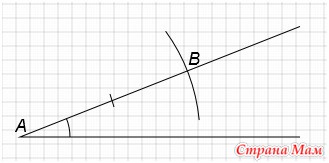
С центром в точке А проведем окружность радиусом равным длине отрезка b. Получим точку C. 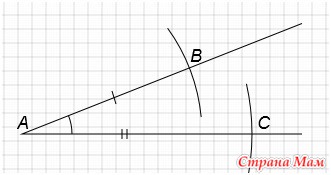
Соединим точки В и С. Получим треугольник АВС.
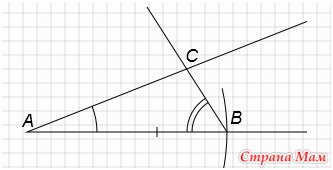
9. Построить треугольник по стороне и двум углам, прилежащим к ней
Дано: отрезок а, угол А1, угол В1 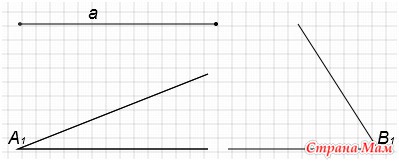
Построим угол А, равный углу А1. (Смотри элементарное построение №4).
С центром в точке А проведем окружность радиусом равным длине отрезка а. Получим точку В. 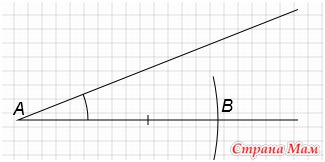
C вершиной в точке В строим угол, равный углу В1. Получим точку С. Получили треугольник АВС.
Удачи в решении задач!
Спасибо за внимание.
Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Уравнение прямой, проходящей через заданную точку параллельно заданной прямой.
Эта статья является развернутым ответом на вопрос: «Как составить уравнение прямой, проходящей через заданную точку плоскости параллельно заданной прямой»? Сначала приведена необходимая теория, после чего разобраны решения характерных задач. В заключении разобрано нахождение уравнений прямой, проходящей через заданную точку трехмерного пространства параллельно заданной прямой.
Навигация по странице.
Видео:Перпендикуляр к прямой через заданную точку.Скачать

Уравнение прямой, проходящей через заданную точку плоскости параллельно заданной прямой.
Чтобы составление уравнения прямой, проходящей через заданную точку плоскости параллельно заданной прямой, не вызвало затруднений, вспомним важные факты.
Аксиома параллельных прямых гласит: на плоскости через точку, не лежащую на заданной прямой, проходит единственная прямая, параллельная данной. Таким образом, мы можем определить конкретную прямую a на плоскости, указав прямую линию b , которой параллельна прямая a , и точку М1 , не лежащую на прямой b , через которую проходит прямая a .
Поставим перед собой следующую задачу.
Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy . Пусть в этой системе координат задана точка 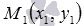
Решим поставленную задачу.
Из условия мы знаем координаты точки М1 , через которую проходит прямая a . Этих данных не достаточно, чтобы написать уравнение прямой a .
Нам еще нужно знать
Как же их найти?
По условию прямая a параллельна прямой b , тогда, на основании необходимого и достаточного условия параллельности двух прямых на плоскости, в качестве направляющего вектора прямой a мы можем принять направляющий вектор прямой b , в качестве нормального вектора прямой a мы можем взять нормальный вектор прямой b , а угловой коэффициент прямой a равен угловому коэффициенту прямой b (или они оба бесконечны).
Таким образом, чтобы в прямоугольной системе координат на плоскости написать уравнение прямой a , проходящей через заданную точку 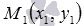
- или координаты направляющего вектора прямой b (
),
- или координаты нормального вектора прямой b (
),
- или угловой коэффициент прямой b (
),
принять их соответственно в качестве
- координат направляющего вектора прямой a (
),
- координат нормального вектора прямой a (
),
- углового коэффициента прямой a (
),
и записать требуемое уравнение прямой a соответственно в виде
или
,
,
.
Внесем ясности – приведем примеры с подробными решениями на каждый случай.
Напишите уравнение прямой, которая в прямоугольной системе координат Oxy на плоскости проходит через точку 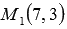
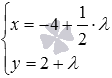
Из параметрических уравнений прямой 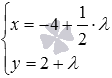
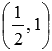
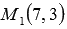
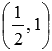
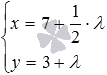
Это и есть искомые уравнения прямой, проходящей через заданную точку 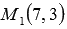
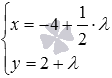
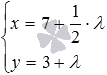
Иногда требуется составить уравнение прямой определенного вида, проходящей через заданную точку плоскости параллельно заданной прямой. В этом случае сначала записываем уравнение прямой, которое проще всего получить, после чего приводим его к нужному виду.
Составьте уравнение прямой в отрезках, если эта прямая в прямоугольной системе координат Oxy проходит через точку плоскости с координатами 
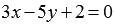
Очевидно, нормальным вектором прямой, общее уравнение которой имеет вид 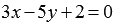
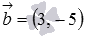

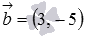
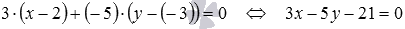

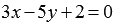
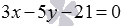
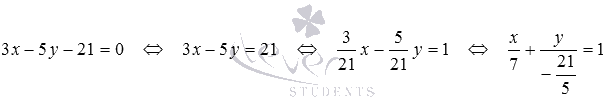
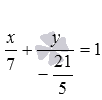
Напишите уравнение прямой, которая в прямоугольной системе координат Oxy на плоскости проходит через точку 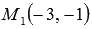
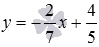
Мы знаем, что угловые коэффициенты параллельных прямых равны (или бесконечны), тогда 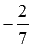
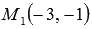
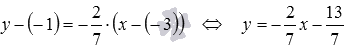
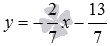
Итак, уравнение прямой a , проходящей через заданную точку плоскости M1 параллельно заданной прямой b , проще всего записывать в таком виде, в котором записано уравнение заданной прямой b .
Видео:6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

Уравнения прямой, проходящей через заданную точку пространства параллельно заданной прямой.
В трехмерном пространстве через точку М1 , не лежащую на прямой b , проходит единственная прямая a , параллельная прямой b . Таким образом, прямую в пространстве можно задать, указав точку, через которую она проходит, и прямую, которой она параллельна.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , задана прямая b некоторыми уравнениями прямой в пространстве и точка 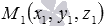
Направляющим вектором прямой a является направляющий вектор прямой b . Таким образом, по известным уравнениям прямой b мы можем определить координаты ее направляющего вектора, а, следовательно, и координаты направляющего вектора прямой a . После этого мы можем записать канонические уравнения прямой a в пространстве и параметрические уравнения прямой a в пространстве, так как известны координаты точки, лежащей на прямой a , и координаты направляющего вектора прямой a .
Рассмотрим решения примеров.
Напишите уравнения прямой, которая проходит через начало прямоугольной системы координат Oxyz в трехмерном пространстве параллельно прямой 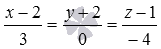
Очевидно, направляющим вектором прямой 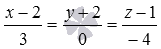
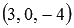
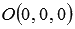
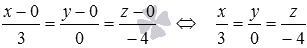
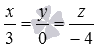
От канонических уравнений прямой a при необходимости можно будет перейти к уравнениям двух плоскостей, пересекающихся по прямой a .
В трехмерном пространстве в прямоугольной системе координат Oxyz заданы три точки 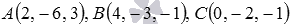
Направляющим вектором прямой, проходящей через точку С параллельно прямой АВ , является вектор 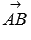
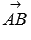
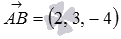
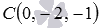
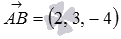
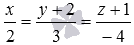
Осталось получить уравнения двух пересекающихся плоскостей, задающих эту прямую:
📺 Видео
Построить прямую параллельную даннойСкачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Уравнение параллельной прямойСкачать

Построение прямой параллельной данной. 6 класс.Скачать
12. Уравнения прямой в пространстве Решение задачСкачать

Задача 3.3. Через точку М провести горизонталь и фронталь.Скачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

ПОСТРОЕНИЕ ПРЯМОЙ ПЕРПЕНДИКУЛЯРНОЙ ДАННОЙ И ПРОХОДЯЩЕЙ ЧЕРЕЗ ДАННУЮ ТОЧКУ. ЗАДАЧИ. ГЕОМЕТРИЯ 7 классСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

4K Как начертить параллельные прямые при помощи циркуля, how to draw parallel linesСкачать
Перпендикулярные прямыеСкачать

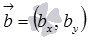 ),
),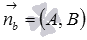 ),
),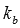 ),
),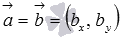 ),
),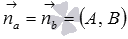 ),
),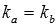 ),
),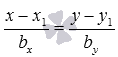 или
или 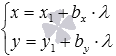 ,
,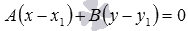 ,
,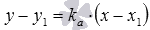 .
.