Как построить прямую параллельную плоскости через точку (8 видео)

Признаки параллельности прямой и плоскости

Признаки параллельности прямой и плоскости имеют следующее определение — прямая m параллельна плоскости α, если в плоскости α можно провести прямую n, параллельную m:

Очевидно через точку пространства, не принадлежащую плоскости, можно провести бесчисленное множество прямых, параллельных данной плоскости.

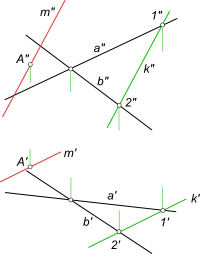
Через точку A провести прямую m, параллельную плоскости α, заданной пересекающимися прямыми a и b

Если нет никаких дополнительных условий, то мы вправе, используя признаки параллельности прямой и плоскости, провести любую прямую из множества прямых, проходящих через точку A и параллельных плоскости α — например параллельно одной из прямых a или b. Если же поставлено условие, чтобы прямая не была параллельна прямым a и b — необходимо построить прямую 12 и провести искомую прямую m(m`, m») параллельно ей.

Через заданную точку A провести плоскость, параллельную прямой f

Плоскость задаем пересекающимися в точке A прямыми a и b. При этом одна из прямых (прямая a) параллельна прямой f.

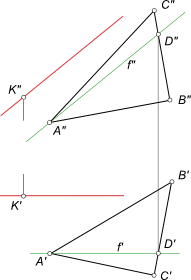
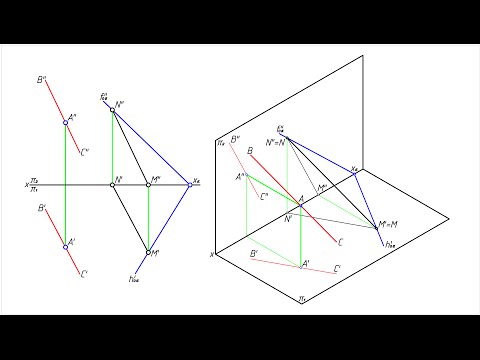
Через заданную точку K провести прямую, параллельную плоскости треугольника ABC и фронтали, проходящей через вершину A

Построим фронталь f по заданному условию: — через точку A` параллельно оси x проводим прямую f`. Данная прямая пересекает B`C` — сторону треугольника в точке D`. По линии связи находим фронтальную проекцию D» точки D, принадлежащей стороне BC треугольника. Проводим через точки A» и D» прямую f». Через точку K проводим прямую параллельную фронтали f. Данная прямая будет параллельна и плоскости треугольника ABC.

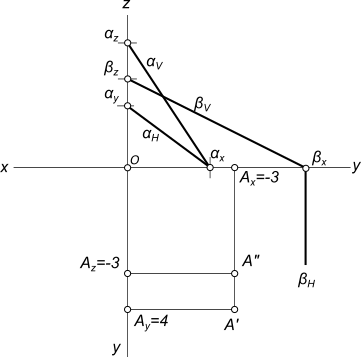
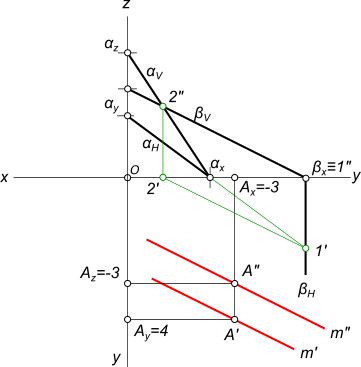
Через точку A(-3;4;-3) провести прямую параллельную двум плоскостям α(3x+4y-2z+7=0) и β(x-2z+5=0)

1. Строим проекции точки A 2. Строим следы плоскости α (3x+4y-2z+7=0): a) z=0; 3x+4y+7=0; αH; y=0; 3x+7=0, x=-7/3, x=-2,33; b) y=0; 3x-2z+7=0; αV; x=0; -2z+7=0, z=3,5; z=0; 3x+7=0, x=-2,33 3) Строим следы плоскости β (x-2z+5=0): βV x=0; -2z+5=0, z=5/2, z=2,5; z=0; x+5=0, x=-5 4) Строим линию пересечения 1—2 заданных плоскостей α и β

5) Строим линию m параллельную плоскостям α и β: m`‖1`—2` и m»‖1″—2″

Видео:Параллельность прямой к плоскостиСкачать

Построение прямой линии параллельно плоскости

Построение прямой, параллельной заданной плоскости, основано на следующем положении, известном из геометрии: прямая параллельна плоскости, если эта прямая параллельна любой прямой в плоскости.

Через заданную точку в пространстве можно провести бесчисленное множество прямых линий, параллельных заданной плоскости. Для получения единственного решения требуется какое-нибудь дополнительное условие.

Например, через точку М (рисунок 140) требуется провести прямую, параллельную плоскости, заданной треугольником ЛВС, и плоскости проекций тс! (дополнительное условие).

Очевидно, искомая прямая должна быть параллельна линии пересечения обеих плоскостей, т. е. должна быть параллельна горизонтальному следу плоскости, заданной треугольником АВС. Для определения направления этого следа можно воспользоваться горизонталью плоскости, заданной треугольником АВС. На рисунке 140 проведена горизонталь DC и затем через точку М проведена прямая, параллельная этой горизонтали.

Поставим обратную задачу: например, надо провести плоскость, параллельную прямой CD, через прямую АВ (рисунок 141).

Прямые АВ и CD — скрещивающиеся. Если через одну из двух скрещивающихся прямых требуется провести плоскость, параллельную другой, то задача имеет единственное решение. Через точку В проведена прямая, параллельная прямой CD; прямые АВ и BE определяют плоскость, параллельную прямой CD.

Как установить, параллельна ли данная прямая данной плоскости? Можно попытаться провести в этой плоскости некоторую прямую параллельно данной прямой. Если такую прямую в плоскости не удается построить, то заданные прямая и плоскость не параллельны между собой.

Можно попытаться найти также точку пересечения данной прямой с данной плоскостью. Если такая точка не может быть найдена, то заданные прямая и плоскость взаимно параллельны.

Видео:Прямая параллельная плоскостиСкачать

Построение взаимно параллельных прямой линии и плоскости и двух плоскостей

Построение взаимно параллельных прямой линии и плоскости. Известно, что если прямая линия (АВ, рис. 4.14) параллельна прямой KL, лежащей в плоскости, то она параллельна этой плоскости.

Для построения прямой, проходящей через заданную точку пространства параллельно заданной плоскости, достаточно провести прямую, параллельную любой прямой, принадлежащей плоскости.

При этом возможно бесчисленное множество решений. Дополнительные требования могут обусловить единственное решение.

В качестве примера на рисунке 4.15 показано построение проекций прямой линии, проходящей через точку с проекциями к’, к, параллельной плоскости треугольника с проекциями a’b’c’, abc и параллельной плоскости V — дополнительное требование. В плоскости треугольника проведена фронталь с проекциями а’1′, а—1. Проекции искомой прямой проведены через проекции к’, к точки параллельно проекциям фронтали к’l’ || а’l’, kl || а—1.

Для того чтобы проверить, параллельна ли прямая заданной плоскости, можно попробовать провести в этой плоскости прямую, параллельную заданной. Если такую прямую в плоскости построить не удается, то заданные прямая и плоскость не параллельны между собой. Можно также попытаться найти точку пересечения данной прямой с данной плоскостью. Если такая точка не может быть найдена, то заданные прямая и плоскость взаимно параллельны.

Построение взаимно параллельных плоскостей. Для такого построения используют известное свойство: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны. Так, например, на рисунке 4.16, а построена плоскость, проходящая через точку с проекциями к’, к, параллельная плоскости, заданной проекциями a’b’, ab и а’с’, ас пересекающихся прямых. Для этого через фронтальную проекцию к’ проведены фронтальные проекции d’k’ || а’с’, е’к’ || a’b’ и через горизонтальную проекцию к — горизонтальные проекции dk || ас, ек || ab. Построенная плоскость, определяемая проекциями k’d ‘, к’е’ и kd, ке, будет параллельна заданной плоскости.

Построение параллельных плоскостей на чертеже удобно выполнять с по-

мощью главных линий плоскости — горизонталей и фронталей. На рисунке 4.16, б плоскость Р задана проекциями a’b’, c’d’ и ab, cd параллельных прямых. Параллельная ей плоскость Т должна проходить через точку с проекциями к’, к. Проекции плоскости Т построены с помощью фронтальных проекций k’f’ фронтали и k’g’ горизонтали и горизонтальных проекций kg горизонтали и kf фронтали. При этом k’f’ || 1′ З’, kg || 1—2.