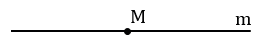Как построить перпендикулярные прямые и параллельные прямые

Примеры:

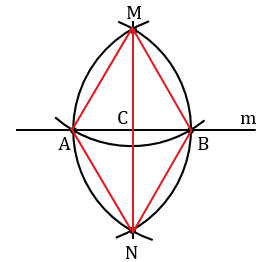
1. Даны прямая и точка на ней. Построить прямую проходящую через данную точку и перпендикулярную к данной прямой.

Дано: прямая m, M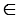m.

Построить: МPm.

Решение:

Произвольно строим с помощью линейки прямую m и отмечаем на ней точку М.

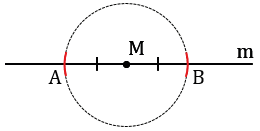
На лучах прямой m, исходящих из точки М, с помощью циркуля откладываем равные отрезки МА и МВ (МА = МВ). Для этого строим окружность с центром в точке М, при этом всю окружность строить не обязательно, достаточно сделать пометки по разные стороны от точки М (смотри выделенное красным).

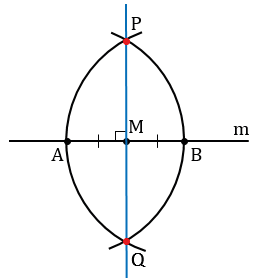
Затем строим две окружности с центрами в точках А и В радиуса АВ (полностью окружности строить необязательно, смотри выделенное фиолетовым и красным цветом).

Данные окружности пересекаются в двух точках, обозначим их Р и Q. Проведем с помощью линейки через точку М и одну из точек Р или Q прямую, например, МР.

Докажем, что прямая МР — искомая прямая, т.е. что МPm.

Рассмотрим треугольник АРВ.

АР = ВР, т.к. по построению это радиусы одинаковых окружностей, следовательно, АРВ — равнобедренный. По построению МА = МВ, т.е. МР — медиана равнобедренного треугольника, тогда по свойству равнобедренного треугольника МР и высота, т.е. МPm. Что и требовалось доказать.

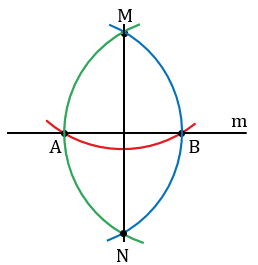
2. Даны прямая и точка не лежащая на этой прямой. Построить прямую проходящую через данную точку и перпендикулярную к данной прямой.

Дано: прямая m, M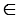m.

Построить: МNm.

Решение:

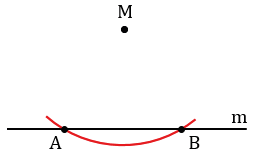
Произвольно строим с помощью линейки прямую m и отмечаем точку М, не лежащую на прямой m.

Далее строим окружность с центром в данной точке М, пересекающую прямую m в двух точках, которые обозначим буквами А и В (всю окружность строить необязательно, смотри выделенное красным цветом).

Затем построим две окружности с центрами в точках А и В, проходящие через точку М (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Эти окружности пересекутся в точке М и еще в одной точке, которую обозначим буквой N. Проведем прямую МN.

Докажем что, прямая МN — искомая, т.е. МNm.

В АМN и ВМN: АМ = АN = ВМ = ВN — радиусы, МN — общая, следовательно, АМN =ВМN (по трем сторонам), значит, углы ВМС и АМС равны (С точка пересечения прямых m и МN). Отсюда следует, что отрезок МС — биссектриса равнобедренного треугольника АМВ (АМ = ВМ — радиусы) с основанием АВ, тогда по свойству равнобедренного треугольника АМ — высота, значит, МNАВ, т.е. МNm.

Поделись с друзьями в социальных сетях:

Видео:Перпендикулярные прямыеСкачать

Прямая. Параллельные и перпендикулярные прямые.

теория по математике 📈 планиметрия

Линия, которую изображают на плоскости при помощи линейки, причем, эта линия не должна быть ограничена точкой ни с одной стороны, называют прямой. Другими словами, прямая не имеет ни начала, ни конца.

Обозначения прямой

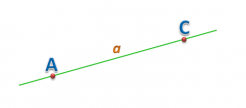
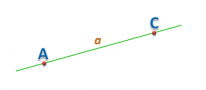
Обычно прямые обозначают прописной латинской буквой или двумя заглавными (если на прямой лежат точки). Рассмотрим это на рисунке. Данную прямую мы можем назвать двумя способами: прямая а; прямая АС.

Рассмотрим теперь две прямые на плоскости. Для них существует два случая расположения: пересекаются и не пересекаются.

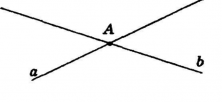
Если две прямые пересекаются, то есть имеют общую точку, то их называют пересекающимися. На рисунке показаны прямые а и b, которые пересекаются в точке A. Запись с помощью символов для данного рисунка выполняют следующим образом: а ∩ b=А, где ∩ — это знак «пересечение».

Если две прямые на плоскости не пересекаются, то их называют параллельными прямыми. На рисунке изображены параллельные прямые. Запись осуществляется следующим образом: a | | b, где | | — знак параллельности.

Признаки параллельности прямых

Рассмотрим прямую с, которая пересекает две прямые а и b и образует с ними восемь углов. Такую прямую с называют — секущая. Пары углов, которые образует секущая, также имеют названия. Итак, на данном рисунке изображены эти все прямые и восемь углов.

Необходимо запомнить названия следующих углов:

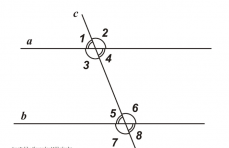
1. накрест лежащие углы: 4 и 5; 3 и 6;
2. односторонние углы: 4 и 6; 3 и 5;
3. соответственные углы: 1 и 5; 3 и 7; 2 и 6; 4 и 8.

С данными углами связаны следующие признаки параллельности прямых:

1. если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны;
2. если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны;
3. если при пересечении двух прямых секущей сумма внутренних односторонних углов равна 180 0 , то прямые параллельны.

Видео:Перпендикулярные прямые. 6 класс.Скачать

Аксиома параллельных прямых

Вспомним, что аксиомой принято называть утверждения, не требующие доказательств.

Через любые две точки на плоскости проходит прямая и притом только одна.

Аксиома №2 Через точку, не лежащую на данной прямой, можно провести только одну прямую параллельную данной.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Следствия из аксиом параллельных прямых

• Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

На данном рисунке видно, что а и b параллельные прямые, с – секущая, она пересекает прямую а в точке А, значит и будет пересекать прямую b в некоторой точке С.

• Если две прямые параллельны третьей, то они параллельны.

По данному рисунку видно, что если прямая CD параллельна АВ и прямая MN параллельна АВ, то CD и MN тоже будут параллельны.

Видео:7 класс, 12 урок, Перпендикулярные прямыеСкачать

Перпендикулярные прямые

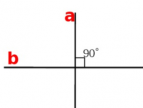
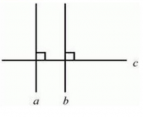
Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.

На рисунке показаны такие прямые а и b. Запись с помощью символов можно сделать следующим образом: а ⊥ b, где « ⊥ » — знак перпендикулярности. Заметим, что две прямые, перпендикулярные к третьей, не пересекаются. На данном рисунке а ⟂ с, b ⟂ c. Видно, что прямые а и b не пересекаются, то есть они – параллельны.

Видео:Тема ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕСкачать

Построение параллельных прямых

Вы будете перенаправлены на Автор24

В основе способов построения параллельных прямых с помощью различных инструментов лежат признаки параллельности прямых.

Видео:Перпендикулярные и параллельные прямые. Математика 6 классСкачать

Построение параллельных прямых с помощью циркуля и линейки

Рассмотрим принцип построения параллельной прямой, проходящей через заданную точку, с помощью циркуля и линейки.

Пусть дана прямая и некоторая точка А, которая не принадлежит данной прямой.

Необходимо построить прямую, проходящую через заданную точку $А$ параллельно данной прямой.

На практике зачастую требуется построить две или более параллельных прямых без данной прямой и точки. В таком случае необходимо начертить прямую произвольно и отметить любую точку, которая не будет лежать на данной прямой.

Рассмотрим этапы построения параллельной прямой:

1. Выберем произвольную точку на данной прямой и назовем ее $В$. обратим внимание, что выбор точки абсолютно произвольный, т.к. не влияет на результат построения.
2. С помощью циркуля и начертим окружность радиуса $АВ$ с центром в точке $В$.

На пересечении окружности и прямой отметим точку и назовем ее $С$.

С тем же радиусом $АВ$ построим окружность с центром в точке $С$. Обратим внимание, что вторая построенная окружность обязательно должна пройти через точку В при правильном выполнении построения.

С прежним радиусом $АВ$ построим третью окружность с центром в точке $А$.

Отметим точку пересечения второй и третьей построенных окружностей и назовем ее $D$. Отметим, что третья окружность при правильном построении также должна пройти через точку $В$.

Через точки $А$ и $D$ проведем прямую, которая будет параллельной заданной.

Таким образом, получили параллельные прямые $ВС$ и $АD$:

$BC parallel AD$, т. $A in AD$.

На практике также применяют метод построения параллельных прямых с помощью чертежного угольника и линейки.

Готовые работы на аналогичную тему

Видео:6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

Построение параллельных прямых с помощью угольника и линейки

Для построения прямой, которая будет проходить через точку М параллельно данной прямой а, необходимо:

1. Угольник приложить к прямой $а$ диагональю (смотрите рисунок), а к его большему катету приложить линейку.
2. Передвинуть угольник по линейке до тех пор, пока данная точка $М$ не окажется на диагонали угольника.
3. Провести через точку $М$ искомую прямую $b$.

Мы получили прямую, проходящую через заданную точку $М$, параллельную данной прямой $а$:

$a parallel b$, т. $M in b$.

Параллельность прямых $а$ и $b$ видна из равности соответственных углов, которые отмечены на рисунке буквами $alpha$ и $beta$.

Видео:Параллельные прямые. 6 класс.Скачать

Построение параллельной прямой, отстоящей на заданное расстояние от данной прямой

В случае необходимости построения прямой, параллельной заданной прямой и отстоящей от нее на заданном расстоянии можно воспользоваться линейкой и угольником.

Пусть дана прямая $MN$ и расстояние $а$.

1. Отметим на заданной прямой $MN$ произвольную точку и назовем ее $В$.
2. Через точку $В$ проведем прямую, перпендикулярную к прямой $MN$, и назовем ее $АВ$.
3. На прямой $АВ$ от точки $В$ отложим отрезок $ВС=а$.
4. С помощью угольника и линейки проведем прямую $CD$ через точку $С$, которая и будет параллельной заданной прямой $АВ$.

Если отложить на прямой $АВ$ от точки $В$ отрезок $ВС=а$ в другую сторону, то получим еще одну параллельную прямую к заданной, отстоящую от нее на заданное расстояние $а$.

Видео:Параллельные и перпендикулярные прямые.Скачать

Другие способы построения параллельных прямых

Еще одним способом построения параллельных прямых является построение с помощью рейсшины. Чаще всего данный способ используют в чертежной практике.

При выполнении столярных работ для разметки и построения параллельных прямых, используется специальный чертежный инструмент – малка – две деревянные планки, которые скрепляются шарниром.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 22 07 2021

📸 Видео

Параллельные прямые циркулемСкачать

Построение перпендикулярных прямыхСкачать

КАК ПОСТРОИТЬ ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ? Примеры | МАТЕМАТИКА 6 классСкачать

Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Как построить две взаимно перпендикулярные прямые с помощью циркуляСкачать

Как провести множество параллельных или перпендикулярных прямых без транспортира?Скачать

Построение параллельных прямыхСкачать

Геометрия 7 класс (Урок№7 - Перпендикулярные прямые.)Скачать

6 класс, 43 урок, Перпендикулярные прямыеСкачать

Построение перпендикуляра к прямойСкачать

Урок ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕСкачать