Как построить поворот четырехугольника (4 видео)

Урок геометрии по теме «Поворот»

Содержание

Презентация к уроку
Параллельный перенос и поворот
Параллельный перенос
Поворот
Готовые работы на аналогичную тему
Примеры задач на параллельный перенос и поворот
Поворот. Задачи
📺 Видео

Презентация к уроку

Цели урока:

Образовательные

ввести понятие поворота и доказать, что поворот есть движение;
рассмотреть поворот отрезка, в зависимости от центра поворота (центр поворота лежит вне отрезка, на отрезке и является одним из концов отрезка);
научить построению отрезка при повороте его на данный угол;
проверить усвоение материала, изученного на предыдущих уроках и материала, пройденного на этом уроке.

Развивающие

развивать умение анализировать условие задачи, строить логическую цепочку при решении задач, обоснованно делать выводы;
развивать мыслительный процесс, познавательный интерес, математическую речь учащихся;

Воспитательные

воспитывать внимательность, наблюдательность, положительное отношение к обучению.

Содержание темы: урок по геометрии разработан для учащихся 9 класса.

Тип урока: урок изучения нового материала и промежуточного контроля усвоения учащимися пройденного на этом уроке и изученного ранее материала.

Организационные формы общения: коллективная, индивидуальная, фронтальная, в парах.

Структура занятия:

Мотивационная беседа с учащимися с последующей постановкой целей;
Проверка домашнего задания;
Актуализация опорных знаний;
Обогащение знаний;
Закрепление изученного материала;
Проверка усвоения изученного материала (тестирование с последующей взаимопроверкой);
Подведение итога занятия (рефлексия);
Домашнее задание.

Оформление: мультимедийный проектор, экран, ноутбук, компьютерная презентация, сигнальные карточки.

Мотивационная беседа.

Без движения — жизнь только летаргический сон.
Жан Жак Руссо

I. Сообщение темы, целей и хода урока. (СЛАЙД 2)

— Ребята, Вы знаете какую важную роль имеет движение в жизни человека, общества, науки. Большую роль играет движение и в математике: преобразование графиков, отображение точек, фигур, плоскостей – всё это движение. На предыдущих уроках мы с Вами рассмотрели несколько видов движения. Сегодня мы познакомимся ещё с одним видом движения: поворотом. Тема урока: поворот.

И наш урок тоже является примером движения, только движения не с физической точки зрения, а движением в умственном развитии, познании нового и приобретения новых знаний. В течение всего урока Вы будете выполнять различные задачи, тесты. Поэтому будьте активны, продвигайтесь в своих знаниях вперёд на протяжении всего урока и улучшайте свои результаты от одного этапа к другому!

В течение всего урока, как мою речь, так и вашу будет сопровождать презентация, которая поможет проверить правильность выполнения Вами домашней работы, предложенных тестов и самостоятельно решённых задач.

II. Проверка домашнего задания.

С помощью СЛАЙДОВ 3-5 проверить решение № 1165.

III. Актуализация опорных знаний.

Тест №1. (СЛАЙДЫ 6-13)

После выполнения теста ребята обмениваются тетрадями и выполняют взаимопроверку.

IV. Изучение нового материала. (обогащение знаний)

(СЛАЙД 14) Отметим на плоскости точку О (неподвижная точка), и зададим угол a – угол поворота. Поворотом плоскости вокруг точки О на угол a называется отображение плоскости на себя, при котором каждая точка M отображается в такую точку M₁, что OM =OM₁ и угол MOM₁ = a.

(СЛАЙД 15) При этом точка O остаётся на месте, т.е. отображается сама в себя, а все остальные точки поворачиваются вокруг точки O в одном и том же направлении на угол a по часовой стрелки или против часовой стрелки.

(СЛАЙД 16) Точка О называется центром поворота, a – угол поворота. Обозначается Р_о a .

(СЛАЙД 17) Если поворот выполняется по часовой стрелке, то угол поворота a считается отрицательным. Если поворот выполняется против часовой стрелки, то угол поворота – положительный.

— Ребята, давайте вспомним понятие движения. Как Вы думаете, является ли поворот движением? (высказывают предположения)

— Поворот – является движением, т.е. отображением плоскости на себя. Докажем это.

(СЛАЙД 18 или СЛАЙД 19)

(Доказательство может выполнить сильный ученик по СЛАЙДУ 18. В этом случае можно сразу после доказательства перейти к СЛАЙДУ 20. Доказательство может выполнить учитель вместе с классом по СЛАЙДУ 19, на котором отображаются этапы доказательства.)

V. Закрепление изученного материала.

Задание. Построить точку M₁, которая получается из точки M поворотом на угол 60 o . Поэтапно с помощью слайда 20 прорабатывается построение точки M₁.

— Какие инструменты нам понадобятся для того, чтобы выполнить поворот? (линейка, циркуль, транспортир)

— Ребята, что сначала нужно отметить? (точку M и центр поворота – точку O)

— Как задаём центр поворота? Отмечаем в определённом месте? (нет, произвольно)

— Как будем выполнять поворот по часовой или против часовой стрелки? Почему? (против, т.к. угол положительный)

— Что нужно построить, чтобы отложить угол 60 o ? (луч OM)

— Как найти на второй стороне угла точку M₁? (с помощью циркуля отложить отрезок OM₁=OM)

— Рассмотрим, как выполняется поворот отрезка в зависимости от расположения центра поворота.

— Рассмотрим случай, когда центр поворота лежит вне отрезка. Решим № 1166 (а). (Если класс сильный, то можно вместе с детьми составить план решения задачи, дать задание решить № 1166 (а) самостоятельно. Решение проверить с помощью СЛАЙДА 21. Если ребята затрудняются с выполнением задания, то решать коллективно, опираясь на СЛАЙД 21)

Работа в парах.

Задание. Построить фигуру, которая получится при повороте отрезка AB на угол — 100 o вокруг точки А.

— Какая точка является центром поворота? Что можно о ней сказать? (это один из концов отрезка – точка А, она будет неподвижной, оставаться на месте)

— Как будем выполнять поворот по часовой стрелки или против часовой? (по часовой, т.к. угол отрицательный)

— Составьте план решения задачи.

Задание выполняют по парам. Проверяют решение с помощью СЛАЙДА 22.

Индивидуальная работа.

Задание. Построить фигуру, в которую переходит отрезок AB при повороте на угол – 100 o вокруг точки О – середины отрезка AB.

— Составьте план решения задачи. Задание выполняют самостоятельно, решение проверяем с помощью СЛАЙДА 23.

— Сегодня на уроке мы рассмотрели поворот отрезка в зависимости от расположения центра поворота. На следующих уроках мы рассмотрим повороты других фигур. (продемонстрировать СЛАЙДЫ 24-25)

VI. Проверка усвоения изученного материала.

Тест №2. (СЛАЙДЫ 26-30)

VII. Подведение итога урока. (рефлексия)

— Ребята, давайте выделим тех, кто был лучшим на каждом этапе. (подводится итог, выставляются оценки)

— Поднимите руки, кому понравился урок. Отметьте, что интересного было на уроке?

VII. Домашнее задание.

№ 1166 (б), № 1167 – для тех, кто получил оценку “3”.
№ 1167 (рассмотреть три случая расположения центра поворота: центр — вершина А, центр расположен вне треугольника, центр лежит на стороне АВ треугольника) – для тех, кто получил оценку “4” и “5”.

Видео:Поворот фигуры. Построить поворот фигур вокруг точки на угол по часовой или против часовой стрелкиСкачать

Параллельный перенос и поворот

Вы будете перенаправлены на Автор24

Видео:ПоворотСкачать

Параллельный перенос

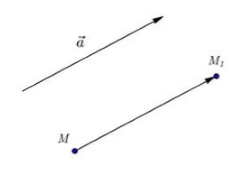
Введем определение параллельного переноса на вектор. Пусть нам дан вектор $overrightarrow$.

Рисунок 1. Параллельный перенос

Введем следующую теорему.

Параллельный перенос является движением.

Доказательство.

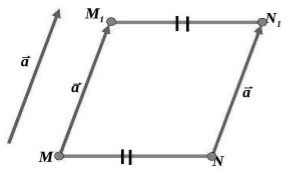
Пусть нам даны точки $M и N$. Пусть при их параллельном переносе на вектор $overrightarrow$ эти точки отображаются в точки $M_1$ и $N_1$, соответственно (рис. 2).

Рисунок 2. Иллюстрация теоремы 1

Значит четырехугольник $_1N_1N$ — параллелограмм и, следовательно, $MN=M_1N_1$. То есть параллельный перенос сохраняет расстояние между точками. Следовательно, параллельный перенос является движением.

Теорема доказана.

Видео:Геометрия 9 класс (Урок№30 - Поворот.)Скачать

Поворот

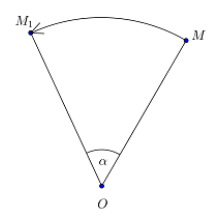
Введем определение поворота вокруг точки $O$ на угол $alpha $.

Поворот вокруг точки $O$ на угол $alpha $ — отображение плоскости на себя, при котором любая точка $M$ отображается на точку $M_1$ такую, что $_1=OM, angle M_1=angle alpha $ (Рис. 3).

Рисунок 3. Поворот

Готовые работы на аналогичную тему

Введем следующую теорему.

Поворот является движением.

Доказательство.

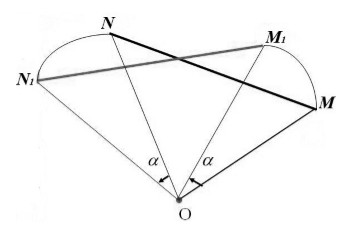
Пусть нам даны точки $M и N$. Пусть при их повороте вокруг точки $O$ на угол $alpha $ они отображаются в точки $M_1$ и $N_1$, соответственно (рис. 4).

Рисунок 4. Иллюстрация теоремы 2

Так как, по определению 2, $_1=OM, _1=ON$ и $overrightarrow<_1>=overrightarrow$, а ,$angle MON=angle M_1ON_1$, то

Следовательно, $MN=M_1N_1$. То есть поворот сохраняет расстояние между точками. Следовательно, поворот является движением.

Теорема доказана.

Видео:9 класс, 33 урок, ПоворотСкачать

Примеры задач на параллельный перенос и поворот

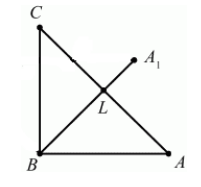
Построить треугольник $A_1B_1C_1$,образованный поворотом вокруг точки $B$ на угол $^0$ равнобедренного прямоугольного (с прямым углом $B)$ треугольника $ABC$.

Решение.

Очевидно, что точка $B$ перейдет сама в себя, то есть $B_1=B$. Так как поворот производится на угол, равный $^0$, а треугольник $ABC$ равнобедренный, то прямая $BA_1$ проходит через точку $L$ — середины стороны $AC$. По определению, отрезок $BA_1=BA$. Построим его (Рис. 5).

Построим теперь вершину $C_1$ по определению 2:

[angle CBC_1=^0, BC=BC_1]

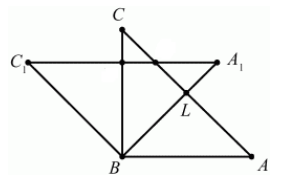
Соединим все вершины треугольника $A_1B_1C_1$ (Рис. 6).

Решение закончено.

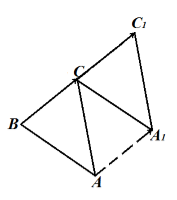
Построить параллельный перенос треугольника $ABC$ на вектор $overrightarrow$.

Решение.

Перенесем каждую вершину треугольника на вектор $overrightarrow$. Получаем треугольник $CA_1C_1$ (рис. 7).

Решение закончено.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 15 04 2021

Видео:Четырехугольник.Поворот фигуры.aviСкачать

Поворот. Задачи

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Это занятие будет посвящено теме «Поворот». Мы решим несколько задач на упомянутую тему, но для начала повторим понятие движения. После чего рассмотрим один из видов движения – поворот, перечислим его свойства и особенности. Решим вместе с преподавателем задачи на эту тему.

Если у вас возникнет сложность в понимании тему, рекомендуем посмотреть урок «Связь числа и геометрии. Часть 1. Измерения в геометрии. Свойства фигур»