Видео:Как строить сечения параллелепипедаСкачать
Объем параллелепипеда, построенного на векторах онлайн
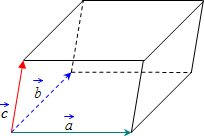
Объём параллелепипеда равен смешанному произведению векторов на которых он построен:
Поскольку смешанное произведение векторов, может быть отрицательным числом, а объём геометрического тела — всегда число положительное, то при вычислении объёма параллелепипеда, построенного на векторах, результат смешанного произведения берется по модулю:
Таким образом, для того, чтобы вычислить объём параллелепипеда, построенного на векторах, нужно найти смешанное произведение данных векторов, и полученный результат взять по модулю.
Наш онлайн калькулятор, найдет площадь параллелепипеда с описанием подробного хода решения на русском языке.
Видео:10 класс, 44 урок, Правило параллелепипедаСкачать
Вектор. Смешанное произведение векторов.
Также его называют тройным скалярным произведением векторов, скорее всего это связано с тем,
что результат — это скаляр (точнее — псевдоскаляр).
Смешанное произведение векторов — скалярное произведение вектора 
на векторное произведение векторов 
и 
.
Или другими словами:
Смешанным произведением векторов 
является число 
, состоящее из скалярного произведения вектора на векторное произведение векторов и . Смешанное произведение
векторов записывается следующим образом:
Геометрический смысл смешанного произведения векторов.
Геометрический смысл смешанного произведения векторов: если три вектора 
правые, то их
смешанное произведение равно объему параллелепипеда построенного на них:
.
В случае левой тройки , смешанное произведение указанных векторов равно объему
параллелепипеда со знаком “–“:
.
Если , и компланарны, то их смешанное произведение = 0.
Вывод: объем параллелепипеда, построенного на векторах , и равен модулю смешанного
произведения этих векторов:
Объем пирамиды, построенной на этой тройке этих векторов, находим по формуле:
Геометрические свойства смешанного произведения векторов.
1. Модуль смешанного произведения некомпланарных векторов равен объему 
параллелепипеда, построенного на этих векторах. Произведение 
будет со знаком плюс, если
тройка векторов — правая, и будем иметь отрицательный знак, если тройка — левая,
2. Смешанное произведение =0 тогда и только тогда, когда векторы компланарны:
векторы компланарны.
Алгебраические свойства смешанного произведения векторов.
1. При перемене мест двух множителей смешанное произведение меняет знак на противоположный:
При циклической (круговой) перестановке множителей смешанное произведение остается без изменений:
2. Смешанное произведение линейно по любому множителю.
Первое свойство следует из первого геометрического свойства и свойств ориентации троек векторов, так
как от перестановки двух множителей местами, модуль смешанного произведения остается прежним, а
изменяется только ориентация тройки. При циклической перестановке векторов ориентация тройки
остается без изменений.
Второе свойство следует из линейности скалярного произведения и первого свойства.
Формула вычисления смешанного произведения векторов.
Теорема (формула вычисления смешанного произведения векторов):
Если у векторов в правом ортонормированном базисе 
координаты
, 
,
соответственно, то смешанное произведение их вычисляется по следующей формуле:
Из определения следует:
что и требовалось доказать.
Еще некоторые свойства смешанного произведения векторов.
1. 
2. 
3 .Три вектора компланарны в том случае, если 
4. Тройка векторов будет правой только если 
. Ежели 
, то векторы, и
создают левую тройку векторов.
5. 
6. 
7. 
8. 
9. 
10. Тождество Якоби: 
Если векторы 
, 
и 
заданы своими координатами, то их
смешанное произведение можно найти по формуле, приведенной ниже:
Видео:Правило параллелепипеда для векторовСкачать
Правило параллелепипеда. Разложение вектора
Вы будете перенаправлены на Автор24
Видео:№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать
Правило параллелепипеда
Для правила сложения трех векторов рассмотрим следующую задачу.
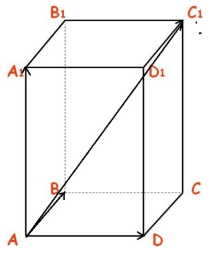
Дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Доказать, что $overrightarrow+overrightarrow+overrightarrow=overrightarrow$
Доказательство.
Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:
Так как $overrightarrow=overrightarrow, overrightarrow=overrightarrow$
Из этой задачи получаем следующее правило для нахождения сложения трех векторов. Чтобы найти сумму трех векторов $overrightarrow,overrightarrow и overrightarrow$ нужно от произвольной точки $O$ отложить векторы $overrightarrow=overrightarrow$, $overrightarrow=overrightarrow$ и $overrightarrow=overrightarrow$ и построим параллелепипед на этих векторах. Тогда вектор диагонали $overrightarrow$ и будет суммой этих трех векторов. Это правило называется правилом параллелепипеда для сложения трех векторов.
Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать
Разложение вектора по двум неколлинеарным векторам
Вспомним сначала, какие векторы называются компланарными.
Два вектора, которые параллельны одной плоскости называются компланарными.
Произвольный вектор $overrightarrow
$ можно разложить по трем некомпланарным векторам $overrightarrow, overrightarrow$ и $overrightarrow$ с единственными коэффициентами разложения.
Математически это можно записать следующим образом
Доказательство.
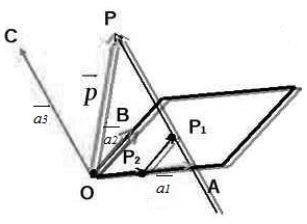
Существование: Пусть нам даны три некомпланарных вектора $overrightarrow, overrightarrow$ и $overrightarrow$. Выберем произвольную точку $O$ и построим следующие векторы:
[overrightarrow=overrightarrow, overrightarrow=overrightarrow, overrightarrow=overrightarrow и overrightarrow
=overrightarrow]
Рассмотрим следующий рисунок:
Произведем следующие дополнительные построения. Проведем через точку $P$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает плоскость $OAB$ в точке $P_1$. Далее, проведем через точку $P_1$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает прямую $OA$ в точке $P_2$ (смотри рисунок выше).
Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:
Так как векторы $overrightarrow$ и $overrightarrow$ коллинеарны, то
Так как векторы $overrightarrow
$ и $overrightarrow$ коллинеарны, то
Так как векторы $overrightarrow
$ и $overrightarrow$ коллинеарны, то
Тогда, получаем, что
Существование разложения доказано.
Единственность: Предположим противное. Пусть существует еще одно разложение вектора $overrightarrow
$ по векторам $overrightarrow, overrightarrow$ и $overrightarrow$:
Вычтем эти разложения друг из друга
Из этого получаем
Теорема доказана.
📽️ Видео
Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать
44. Правило параллелепипедаСкачать
§20 Нахождение объёма параллелипипедаСкачать
СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать
№359. Дан параллелепипед ABCDA1B1C1D1. а) Разложите вектор BD1 по векторам ВА, ВС и ВВ1.Скачать
Сложение векторов. Правило параллелограмма. 9 класс.Скачать
№330. Нарисуйте параллелепипед ABCDA1B1C1D1 и обозначьте векторы C1D1, BA1Скачать
Координаты вектора в пространстве. 11 класс.Скачать
№361. Диагонали параллелепипеда ABCDA1B1C1D1 пересекаются в точке О. Разложите векторыСкачать
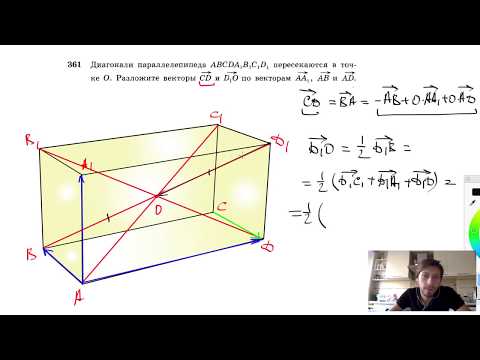
Урок №6 Решение прямого параллелепипеда с помощью векторовСкачать
10 класс, 40 урок, Сложение и вычитание векторовСкачать
Площадь параллелограмма, построенного на данных векторахСкачать
Как построить точки в системе координат OXYZСкачать
ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать
10 класс, 43 урок, Компланарные векторыСкачать
