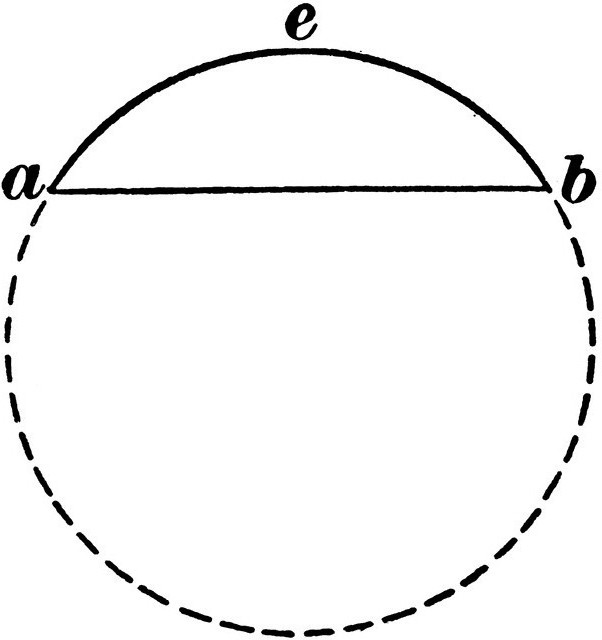
Что такое несовпадающие окружности (4 видео)

Окружность. Относительное взаимоположение окружностей.

Если две окружности имеют только одну общую точку, то говорят, что они касаются.

Если же две окружности имеют две общие точки, то говорят, что они пересекаются.

Трех общих точек две не сливающиеся окружности иметь не могут, потому, что в противном случае через три точки можно было бы провести две различные окружности, что невозможно.

Будем называть линией центров прямую, проходящую через центры двух окружностей (например, прямую OO₁).

Теорема.

Если две окружности имеют общую точку по одну сторону от линии центров, то они имеют общую точку и по другую сторону от этой линии, т.е. такие окружности пересекаются.

Пусть окружности O и O₁ имеют общую точку A, лежащую вне линии центров OO_1. Требуется доказать, что эти окружности имеют еще общую точку по другую сторону от прямой OO₁.

Опустим из A на прямую OO₁ перпендикуляр AB и продолжим его на расстояние BA₁, равное AB. Докажем теперь, что точка A₁ принадлежит обеим окружностям. Из построения видно, что точки O и O₁ лежат на перпендикуляре, проведенном к отрезку AA₁ через его середину. Из этого следует, что точка O одинаково удалена от A и A₁. То же можно сказать и о точке O₁. Значит обе окружности, при продолжении их, пройдут через A₁.Таким образом, окружности имеют две общие точки : A (по условию) и A₁ (по доказанному). Следовательно, они пересекаются.

Следствие.

Общая хорда (AA₁) двух пересекающихся окружностей перпендикулярна к линии центров и делится ею пополам.

Теоремы.

1. Если две окружности имеют общую точку на линии их центров или на ее продолжении, то они касаются.

2. Обратно: если две окружности касаются, то общая их точка лежит на линии центров или на ее продолжении.

Признаки различных случаев относительного положения окружностей.

Пусть имеем две окружности с центрами O и O₁, радиусами R и R₁ и расстоянием между центрами d.

Эти окружности могут находиться в следующих 5-ти относительных положениях:

1. Окружности лежат одна вне другой, не касаясь. В этом случае, очевидно, d > R + R₁ .

2. Окружности имеют внешнее касание. Тогда d = R + R₁, так как точка касания лежит на линии центров O O₁.

3. Окружности пересекаются. Тогда d R + R₁, потому что в треугольнике OAO₁ сторона OO₁ меньше суммы, но больше разности двух других сторон.

4. Окружности имеют внутреннее касание. В этом случае в d = R — R₁, потому что точка касания лежит на продолжении линии OO₁.

5. Одна окружность лежит внутри другой, не касаясь. Тогда, очевидно,

d R + R₁, то окружности расположены одна вне другой, не касаясь.

2. Если d = R + R₁, то окружности касаются извне.

3. Если d R — R₁, то окружности пересекаются.

4. Если d = R — R₁, то окружности касаются изнутри.

5. Если d R Е R₁. Значит, все эти случаи исключаются. Остается один возможный, именно тот, который требовалось доказать. Таким образом, перечисленные признаки различных случаев относительно положения двух окружностей не только необходимы, но и достаточны.

Содержание

Окружность и ее свойства. Длина окружности.
Понятие окружности и ее основные элементы
Длина окружности
Основные свойства
Всё про окружность и круг
📹 Видео

Видео:Окружность. 7 класс.Скачать

Окружность и ее свойства. Длина окружности.

Окружность в математике является фигурой одной из самых главных и важных. Она необходима для множества расчетов. Знания свойств этой фигуры из школьной программы непременно пригодятся в жизни. Длина окружности требуется при расчете многих материалов с круглым сечением. Заниматься чертежами, строить заборчик возле клумбы – для этого понадобится знание геометрической фигуры и ее свойств.

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Понятие окружности и ее основные элементы

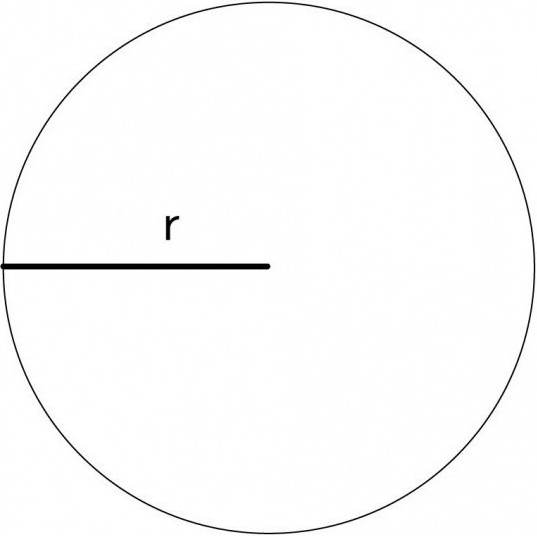
Фигура на плоскости, состоящая из многочисленных точек, расположенных на равном расстоянии от центральной, называется окружностью. Отрезок, выходящий из центра и соединяющий его с одной из точек, образующих окружность, называется радиусом. Хордой является отрезок, который соединяет пару точек, расположенных по периметру круга, между собой. Если она расположена так, что проходит через центральную точку, то одновременно является диаметром.

Длина радиуса окружности равна длине диаметра, уменьшенной вдвое. Пара несовпадающих точек, находящихся на окружности, делят ее на две дуги. Если отрезок с концами в этих точках проходит через центральную точку (тем самым являясь диаметром), то образуемые дуги будут являться полуокружностями.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Длина окружности

Расчет периметра окружности определяется несколькими способами: через диаметр или через радиус. На практике было выявлено, что длина окружности (l) при делении на ее же диаметр (d) всегда дает одно число. Это число π, которое ровняется 3,141692666… Расчет производится по формуле: π= l/ d. Преобразуя ее, получается длина окружности. Формула такова: l=πd.

Для нахождения радиуса применим следующую формулу: d=2r. Это стало возможным, благодаря делению. Ведь радиус — это половина диаметра. Как только получили вышеуказанные значения, можно вычислить, чему же ровна длина окружности, по формуле следующего вида: l=2πr.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Основные свойства

Площадь круга всегда больше, если сравнивать ее с площадями иных замкнутых кривых. Касательная — это прямая, которая соприкасается с окружностью только в одной точке. Если прямая пересекает ее в двух местах, то она является секущей. Точка, в которой 2 различные окружности соприкасаются друг с другом, всегда находится на прямой, проходящей через их центральные точки. Пересекающимися на плоскости являются такие окружности, которые имеют 2 общие точки. Угол между ними рассчитывается как угол, образованный касательными к точкам соприкосновения.

Если через точку, не являющейся точкой окружности, провести две секущиеся к ней прямые, то образованный ими угол будет равен разности длин дуг, уменьшенной вдвое. Данное правило действует и в противоположном случае, когда речь идет о двух хордах. Две пересекающиеся хорды образуют угол, равный сумме длин дуг, уменьшенной в два раза. Дуги в такой ситуации выбирают в данном углу и углу, расположенному напротив. Оптическое свойство окружности гласит следующее: лучи света, отраженные от зеркал, расставленных по периметру круга, собираются обратно в его центр. В данном случае источник света должен быть установлен в центральной точке круга.

Видео:Уравнение окружности (1)Скачать

Всё про окружность и круг

Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.

Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.

Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2

Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.

Квадрат касательной равен произведению секущей на ее внешнюю часть

Центральный угол — это угол, вершина которого совпадает с центром окружности.

Дугой называется часть окружности, заключенная между двумя точками.

Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.

Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.

Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.