Равносторонний треугольник — это самый простой правильный многоугольник из возможных. При нахождении его площади возникают частные варианты его расчета. Важно знать и понимать признаки и свойства этого вида фигур, для более легкого вычисления этого параметра. Все методы, представленные ниже, достаточно просты в применении, и не потребуют глубокого осмысления….
- Признаки и свойства фигуры
- Расчет через сторону
- Расчет по высоте
- Расчет через окружности
- Все формулы для треугольника
- 1. Как найти неизвестную сторону треугольника
- 2. Как узнать сторону прямоугольного треугольника
- 3. Формулы сторон равнобедренного треугольника
- 4. Найти длину высоты треугольника
- равносторонний треугольник площадь, высота, радиус вписанной и описанной
- Всё о равностороннем треугольнике!
- Что такое равносторонний треугольник
- Что из себя представляет равносторонний треугольник!?
- Сколько градусов составляет угол в равностороннем треугольнике!?
- Равносторонний треугольник максимальный угол
- Высота равностороннего треугольника
- Высота равностороннего треугольника формула через сторону
- Площадь равностороннего треугольника
- Радиус окружности, вписанной в равносторонний треугольник
- Почему встречаются две формулы радиуса вписанной окружности!?
- Доказательство первой формулы радиус вписанной окружности равностороннего треугольника
- Доказательство второй формулы радиус вписанной окружности равностороннего треугольника
- Радиус описанной окружности равностороннего треугольника
- Задача : Вписанный квадрат в равносторонний треугольник.
- Решение задачи :
- Периметр равностороннего треугольника формула
- Формула периметра равностороннего треугольника
- Задача : найти высоту равностороннего если известна сторона вписанного квадрата.
- Задача : найти сторону равностороннего треугольника через площадь.
- Ответ задачи : найти сторону равностороннего треугольника через площадь.
- Задача : если радиус описанной окружности в 2 раза больше радиуса вписанной окружности то треугольник равносторонний
Видео:Как найти сторону равностороннего треугольника #shorts | ЕГЭ 2022 по профильной математике | ЭйджейСкачать

Признаки и свойства фигуры
Для того чтобы рассчитать его площадь необходимо понимать свойства и признаки, которыми он обладает. Можно выделить следующие основные признаки этой фигуры:
- Значение величины его углов одинаково во всех случаях и равняется 60 градусам, вне зависимости от размера сторон.
- Биссектриса, высота и медиана выпущенные из одного угла будут совпадать.
- Любая сторона равностороннего треугольника равна двум другим.
- Центр правильного треугольника будет являться центром для вписанной и описанной окружности.
- Является частным случаем равнобедренного треугольника.
Важно! Если хотя бы один из этих признаков соблюдается, значит, треугольник является равносторонним. 
Дополнительно этот частный случай фигуры обладает следующими свойствами:
- Средняя линия, которая делит две боковые стороны пополам, равняется половине основания, параллельно которому она располагается.
- Сумма всех его углов не превышает 180 градусов.
- Радиус вписанной окружности рассчитывается по следующей формуле r =
, а описанной согласно выражению R =
.
- Радиус описанной окружности в правильном треугольнике в 2 раза больше радиуса вписанной.
Видео:Задание 15 ОГЭ. Медиана равностороннего треугольникаСкачать

Расчет через сторону
Существует множество способов расчета площади этой фигуры. Все они имеют свои преимущества и недостатки. Применяются в зависимости от условий, представленных задаче. Самая популярный способ найти искомое значение для равностороннего треугольника вычисляется через произведение половины сторон и синуса угла между ними, выглядит это следующим образом: 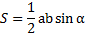
В случае с равносторонним, этот способ упрощается в значительной степени. Для этого нужно обратиться к рассмотренным выше признакам и свойствам. Исходя из того, что все углы этой фигуры равны, и равняются 60 градусам. Синус 60 градусов, согласно таблице Брадиса, равняется 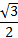
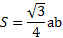
Учитывая то, что все стороны этой фигуры равны, то преобразованное выражение даст такой результат: 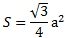
Данная формула отлично подойдет в случае, если известна величина стороны этой фигуры. В таком виде вычислять данный показатель гораздо легче и быстрее.
Те, кто помнит формула Герона, знают, как найти площадь этой фигуры. В процессе преобразования выражение изменится в представленное выше. Площадь этой фигуры по Герону рассчитывается так: 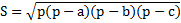
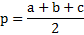
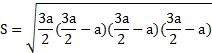
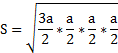
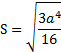
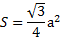
Полученная формула площади и представленные ниже функции могут быть использованы только, в случае, если фигура является правильной, в ином случае не будет давать правильный ответ.
Видео:Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

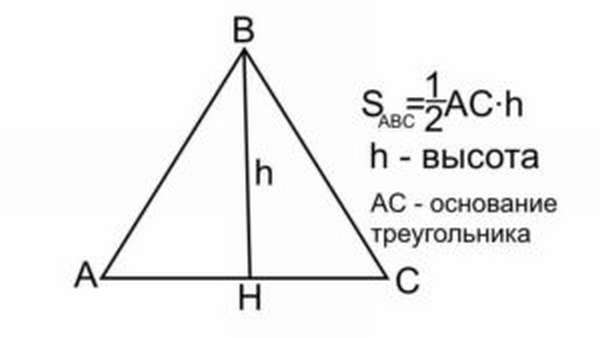
Расчет по высоте
Найти площадь равностороннего треугольника можно также, если известна его высота и сторона. Половина длины высоты умножается на сторону, выбрана может быть любая высота и сторона, ведь согласно свойствам, они все одинаковые: 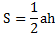
Если в задаче указана информация о том, что треугольник является равносторонним и известна величина высоты. А чему равна длина стороны неизвестно, то можно воспользоваться формулой, позволяющей ее рассчитать. Найти сторону можно разделив двойную величину высоты на корень квадратный из трех, математически выглядит следующим образом: 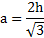
Для того чтобы не делать лишних расчетов можно вывести формулу этого показателя сразу же через высоту. Квадрат высоты делится на корень квадратный из трех. Она будет выглядеть так: 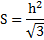
Видео:Задача найти сторону равностороннего треугольника по медианеСкачать

Расчет через окружности
В математике популярен также прием расчета, рассматриваемого в статье, значения через помещение фигуры в окружность или наоборот. Такая окружность называется описанной. Если она находится внутри, то она называется вписанной. Именно в этом разделе возникает большинство вопросов, как найти площадь равностороннего многоугольника с тремя углами.
Описанная окружность обязательно должна проходить через все вершины, вписанная должна проходить через стороны только в одной точке по касательной.
Если в условии задачи дан радиус вписанной и описанной окружности, то из них также можно составить выражение, так как вместе они дадут суммарную длину высоты. Как рассчитывается площадь при ее помощи, показано выше: h = R + r .
Преобразовав формулу 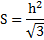
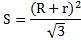
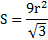
Если же будет дан размер радиуса описанной окружности, то выражение будет выглядеть следующим образом: 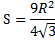
Использование этих свойств пригодится для расчета стороны фигуры. Для того чтобы ее найти можно воспользоваться выражением 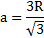
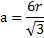
Учитывая радиус описанной окружности можно найти искомое значение при помощи возведения стороны в куб, после чего результат делится на радиус, увеличенный в 4 раза. Математически его можно записать следующим образом: 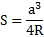
Процесс расчета, чему равен показатель площади равностороннего треугольника через любую из предложенных формул не должен вызывать особых затруднений. Для того чтобы успешно справиться с этой задачей не нужно запоминать все указанные способы, достаточно запомнить основные общие формулы расчета, а также свойства и признаки этой фигуры.
Внимание! Для проверки правильности расчетов можно воспользоваться несколькими способами, результаты должны совпасть.
Площадь равностороннего треугольника
Площадь равностороннего треугольника, вписанного в окружность
Применив логическое мышление, расчеты с легкостью преобразовываются в частные случаи, коих гораздо больше. Нецелесообразно забивать голову большим количеством нерелевантной информации, лучше развивать причинно-следственную связь для преобразования выражений.
Видео:Высота равностороннего треугольника равна 13√3 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Все формулы для треугольника
Видео:Формулы равностороннего треугольника #shortsСкачать

1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a , b , c — стороны произвольного треугольника
α , β , γ — противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
Видео:НАЙДИТЕ ВЫСОТУ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКАСкачать

2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a , b — катеты
c — гипотенуза
α , β — острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
Видео:Урок. Как найти сторону в равностороннем треугольнике. Математика 2 класс. #учусьсамСкачать

4. Найти длину высоты треугольника
Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

a — сторона, основание
b, c — стороны
β , γ — углы при основании
p — полупериметр, p=(a+b+c)/2
R — радиус описанной окружности
S — площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
Видео:№488. Найдите: а) высоту равностороннего треугольника, если его сторона равна 6 см;Скачать

равносторонний треугольник площадь, высота, радиус вписанной и описанной
Что такое равносторонний треугольник, площадь равносторонних треугольников, равносторонние треугольники примеры.
Если все углы треугольника равны то, то это равносторонний треугольник и все стороны у такого треугольника равны.
Видео:Геометрия Найдите сторону равностороннего треугольника, высота которого равна hСкачать
Всё о равностороннем треугольнике!
Видео:Найдите сторону треугольника на рисункеСкачать

Что такое равносторонний треугольник
В равностороннем треугольнике все углы равны аксиома.
На странице виды треугольников, мы упоминали о таком виде треугольников, как равносторонний треугольник.
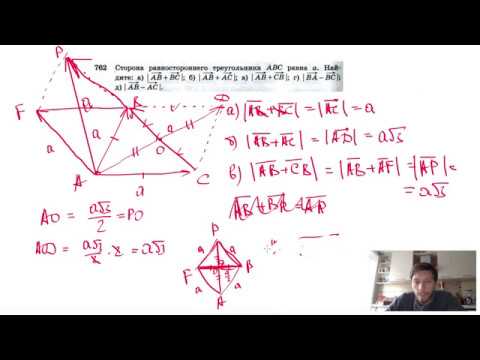
Видео:№762. Сторона равностороннего треугольника ABC равна а. Найдите: а) |AB+BC|Скачать
Что из себя представляет равносторонний треугольник!?
Из самого названия видно, что все стороны данного треугольника равны:
Равносторонний треугольник называют еще правильным.
Какой первый интересный вопрос у вас возникает при виде равностороннего треугольника!?
Видео:Геометрия Равносторонний треугольникСкачать

Сколько градусов составляет угол в равностороннем треугольнике!?
Нет!? Не угадал. жаль. [wall]
Но тем не менее, раз уж вопрос задан, то узнать сколько градусов составляет угол разностороннего треугольника :
180° разделить на 3.
Поскольку у нас треугольник равносторонний. то все углы у такого треугольника будут равны.
Видео:В равностороннем треугольнике ABC высота CH равна 2 √ 3. Найдите стороны этого треугольника.Скачать

Равносторонний треугольник максимальный угол
Поисковый запрос -> «равносторонний треугольник максимальный угол» — не может быть максимальный, минимальный угол в равностороннем треугольнике — потому, что угол в равностороннем треугольнике всегда один!
Видео:№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать

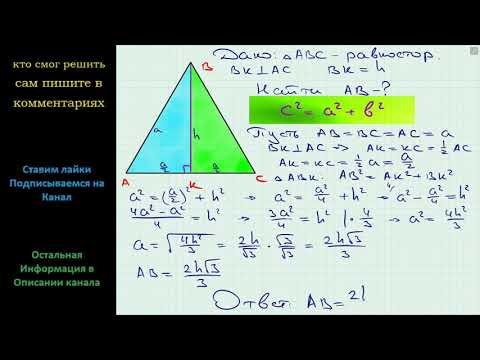
Высота равностороннего треугольника
Формула высоты равностороннего треугольника, если сторону выразить через символ «a», то формула звучит так :
Высота равностороннего треугольника равна , корень из 3 деленное на 2 и умножить на сторону равностороннего квадрата.
Видео:ПЛОЩАДЬ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКА за 20 секунд!Скачать

Высота равностороннего треугольника формула через сторону
Докажем что высота равностороннего треугольника равна — корню из 3, умноженное на сторону и деленное на 2.
Если мы опустим высоту из верхнего угла, то это будет биссектрисой, которая в данном случае не только разделит угол пополам, но и сторону противолежащую.
И если верхний угол будет поделен на 2, то он будет равен :
И если мы прибавим 30 и например оставшийся справа 60, то получим 60 + 30 = 90.
И далее мы можем получить угол между высотой «h» и стороной «a».
И мы получим прямоугольный треугольник, в котором все стороны обозначены.
. и отсюда мы уже можем вывести по теореме пифагора
c² = a² + b² a² = a² 2² + h² = a² 4 + h²
Обе стороны умножим на 4, чтобы избавиться от 4 в дроби :
высоту оставляем одну слева и получаем:
4a² — a² = 4h² -> 4h² = 4a² — a² -> 4h² = 3a² -> h² = 3a²/4
И осталось извлечь квадратный корень из правой стороны.
И далее получаем
Видео:Задание 9 ОГЭ от ФИПИСкачать

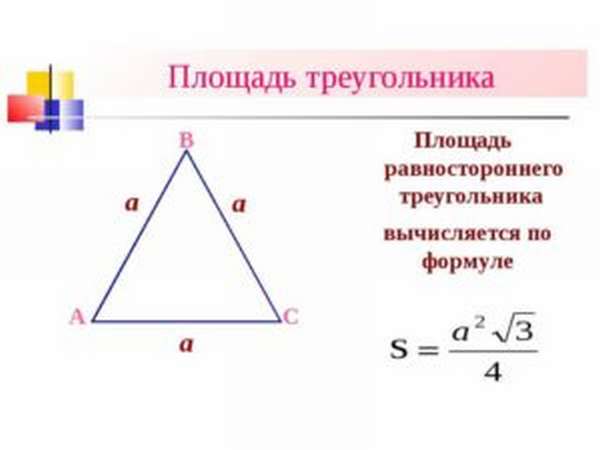
Площадь равностороннего треугольника
Какая формула для площади равностороннего треугольника!?
Площадь равностороннего треугольника равна : корень из 3 деленное на 4, умноженное на сторону в квадрате:
Доказательство очень простое !
Выше мы уже доказали, чему равна высота. возьмем одну сторону треугольника на высоту h.
Вторая сторона будет равна а/2
И далее нам нужно умножить высоту на сторону, поделив на 2. По правилу вычисления площади прямоугольного треугольника.
Мы получаем предварительный результат:
И поскольку у нас два таких треугольника, то правую сторону надо умножить на 2, две двойки сокращаются.
И далее заменим высоту из выше пройденного пункта:
Видео:1747 В равностороннем треугольнике ABC высота CH равна 5 корней из 3Скачать

Радиус окружности, вписанной в равносторонний треугольник

Или вам может встретиться вторая формула вписанной окружности в равносторонний треугольник :
Видео:№258. Из середины D стороны ВС равностороннего треугольника ABC проведен перпендикулярСкачать

Почему встречаются две формулы радиуса вписанной окружности!?
Потому, что они выводятся разными путями, хоть они и не похожи — но это одинаковые значения.
Сможете доказать самостоятельно выше озвученный тезис?
Доказательство первой формулы радиус вписанной окружности равностороннего треугольника
Соотношение радиуса вписанной и описанной окружностей 1 : 2(на момент написания данной страницу мы еще это не прошли на сайте)
Отсюда мы получаем, что :
Подставляем ранее выведенную высоту
r = 1 3 * √ 3 2 a = √ 3 6 a
Доказательство второй формулы радиус вписанной окружности равностороннего треугольника
Не будем здесь доказывать, что два треугольника «ABM» и «AOK» подобные и отличаются в своих размерах и других показателях на коэффициент «Х».
Из этого мы можем создать зависимость:
«r» — относится к отрезку «AK», как «BM» к «AM»
«AK» и «BM» равны одному и тому же а/2.
«AM» — это у нас высота — «h».
Далее мы можем записать эту зависимость как :
Как вы знаете, что при делении подобные выражения ведут себя не так, как при умножении(скоро и про это напишем), поэтому заменим деление на умножение:
r * 2 а = а 2 * 1 h
Теперь мы можем избавиться в левой стороне от дроби 2/а, умножив две стороны на а/2 :
r = а 2 * а 2 * 1 h
В последней дроби заменяем «h» на наши значение из пункта 2 и поскольку получается опять деление, меняем знак и переворачиваем дробь( см.: деление дробей)
r = а 2 * а 2 * 1 h = а 2 * а 2 * 2 √ 3 * а
r = а 2 * а 2 * 2 √ 3 * а
И в итоге получаем :
Радиус описанной окружности равностороннего треугольника
С описанной окружностью доказывается аналогично, лишь с той разницей, что радиус больше в два раза:

Задача : Вписанный квадрат в равносторонний треугольник.
Докажите, что вписанный квадрат в равносторонний треугольник делит одним углом, сторону треугольника пополам или не делит.
Решение задачи :
Мы знаем, что в равностороннем треугольнике все углы равны 60 :
И если мы посмотрим на треугольник ABC , то поскольку, все углы данного разностороннего треугольника равны 60°,
То стороны у этого треугольника будут равны между собой.
И одна из сторон совпадает со стороной квадрата.
Поэтому сторона » AB » равна стороне квадрата » BC » и стороне » BE «
Но » BE » не равна » BD «. Катет всегда будет меньше гипотенузы.
Если » BE » не равно » BD «, то » BD » не равно » AB «, что означает, что точка B не находится в середине отрезка » AD «.
Отсюда мы делаем вывод :
Угол вписанного квадрата не делит сторону равностороннего треугольника пополам!
Периметр равностороннего треугольника формула
Напишите «формулу периметра равностороннего треугольника»:
Обозначается периметр буквой P
Сторону обозначим через — а
Поскольку все стороны у равностороннего треугольника равны,
то периметр равностороннего треугольника будет равен :
3 умноженное на сторону а треугольника:
Формула периметра равностороннего треугольника
Конечно, можно еще представить данную формулу таким образом:
Но такого написания, я никогда не встречал.
Задача : найти высоту равностороннего если известна сторона вписанного квадрата.
Известна сторона «CB» вписанного квадрата, требуется найти высоту равностороннего треугольника «AM».
В пункте №6 и подпункте 4, мы вывели, что :
Сторона «AB» равна стороне квадрата «BC» и стороне «BE»
Поэтому, высота «AN» маленького треугольника будет равна :
И далее мы уже можем вывести высоту треугольника :
Задача : найти сторону равностороннего треугольника через площадь.
Известна площадь равностороннего треугольника «S», требуется узнать его сторону «а».
Я уже вывел площадь равностороннего треугольника в этом пункте, там же было доказательство!
Нам понадобится данная формула для решения выше озвученной задачи!
Нам всего-то навсего нужно выразить сторону «а» через «S»
Умножаем обе стороны на
Справа, в выражении дробь сократится, а слева появится данная дробь в перевернутом виде:
Далее, чтобы получить сторону через площадь, нам нужно извлечь корень :
Преобразуем еще раз:
Ответ задачи : найти сторону равностороннего треугольника через площадь.
Сторона равностороннего треугольника равна корню из площади умноженное на 2, и деленное на корень 4 степени из 3.
Задача : если радиус описанной окружности в 2 раза больше радиуса вписанной окружности то треугольник равносторонний
Повстречал вот такой поисковый запрос :
«если радиус описанной окружности в 2 раза больше радиуса вписанной окружности то треугольник равносторонний«
Данную формулировку можно перефразировать и будет выглядеть совсем по другому:
Докажите, что радиус вписанной окружности равностороннего треугольника больше в два раза, радиуса описанной окружности
А почему, вы узнаете дальше.
Для доказательства данного утверждения нам понадобится :
Радиус вписанной окружности равностороннего треугольника, о котором я рассказывал здесь :
И второе — это радиус вписанной окружности равностороннего треугольника, о котором я рассказывал здесь : :
Далее — нужно разделить больший радиус на меньший:
Как вы наверное знаете, что при делении одной дроби н вторую существует правило, по которому вторую дробь нужно перевернуть и знак будет умножить.
После этого, смотрим, что можно сократить
Сокращаются квадратный корень из 3.
6 и 3, сокращаются только на 3. Сверху остается 2.
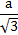 , а описанной согласно выражению R =
, а описанной согласно выражению R = 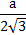 .
.






































