Как построить годограф вектора (8 видео)

ПОСТРОЕНИЕ ГОДОГРАФА КОМПЛЕКСНОЙ ФУНКЦИИ

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ. 4

ВЫЧИСЛЕНИЕ ДРОБНОЙ СТЕПЕНИ КОМПЛЕКСНОГО ЧИСЛА 4

ПОСТРОЕНИЕ ГОДОГРАФА КОМПЛЕКСНОЙ ФУНКЦИИ. 5

3. РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
С ИСПОЛЬЗОВАНИЕМ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ. 6

4. РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
КЛАССИЧЕСКИМ СПОСОБОМ. 7

ОФОРМЛЕНИЕ. 7

БИБЛИОГРАФИЧЕСКИЙ СПИСОК. 8

ПРИЛОЖЕНИЕ. Варианты заданий расчетной работы. 9

ВВЕДЕНИЕ

Расчетная работа проводится по первому разделу дисциплины «Основы теории управления» и предусматривает выполнение следующих вычислений, позволяющих студентам восстановить свои знания и умения по разделам математики, используемым в данной дисциплине:

1) расчет и изображение на плоскости дробной степени комплексного числа;

2) расчет и изображение на комплексной плоскости годографа комплексной функции;

3) решение дифференциального уравнения с использованием операционного исчисления;

4) решение дифференциального уравнения классическим способом.

Каждый студент получает индивидуальный вариант задания (приведены в приложении) и выполняет его в установленный срок – 2 недели.

ВЫЧИСЛЕНИЕ ДРОБНОЙ СТЕПЕНИ КОМПЛЕКСНОГО ЧИСЛА

Предлагается вычислить и изобразить на плоскости все числа

Удобно использовать показательную форму комплексного числа

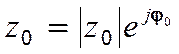
При определении j₀ лучше всего изобразить это число в виде вектора и использовать полное значение аргумента в пределах 0-2p, а не только главное значение, которое дают стандартные тригонометрические функции.

Затем определяется целая степень (положительная или отрицательная) числа z₀ , которая дает одно число:

На последнем этапе определяется корень n-й степени, который дает n значений:

Все n чисел должны быть показаны в виде векторов на комплексной плоскости.

ПОСТРОЕНИЕ ГОДОГРАФА КОМПЛЕКСНОЙ ФУНКЦИИ

Предлагается изобразить график комплекснозначной функции вещественного аргумента w на комплексной плоскости при изменении этого аргумента от 0 до ¥. Такой график называют годографом функции, который представляет траекторию конца вектора комплексной функции при изменении параметра wÎ[0,¥). График должен иметь качественный вид, отражать начало, примерное прохождение и окончание функции.

Функции являются дробно-рациональными. Удобно представить их в виде произведения более простых функций и в показательной форме. Построить годографы этих составляющих, а затем объединить их в итоговый годограф, учитывая, что при умножении модули также перемножаются, а аргументы складываются.

Поясним на небольшом примере

Годограф первой функции на комплексной плоскости выглядит как прямая линия, начинающаяся в точке 2 на вещественной оси и уходящая вертикально вверх.

Годограф второй составляющей строится в два этапа: сначала один знаменатель (jw-1), что дает аналогичный годограф, только начинающийся из точки –1, затем берем обратную функцию, что при показательном представлении означает следующее: модуль будет обратным и меняться от 1 до 0 (у знаменателя от 1 до ¥), а у аргумента будет меняться знак от –180° до –90° ( у знаменателя от 180 до 90). Таким образом, годограф z₂ представляет полуокружность.

Объединяем z₁ и z₂ : модули перемножаем, фазы складываем, получаем полуокружность с начальным модулем 2, фазой –180°, и конечным модулем 1, фазой 0°. Угол меняется против часовой стрелки. Здесь же покажем и z₃ : сначала jw – годограф проходит по мнимой оси в положительном направлении, а затем обратную, так как z₃ = 1/ jw : модуль меняется от ¥ до 0, а фаза постоянна и равна -90°.

На последнем этапе объединяем z₁z₂ и z₃: можно z₁z₂ повернуть на -90°, начальный модуль устремить к ¥, фаза -270°, конечный модуль будет равен 0, а фаза -90°. Качественный вид итогового годографа показан ниже.

3. РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
С ИСПОЛЬЗОВАНИЕМ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ

Основным достоинством операционного исчисления является возможность алгебраизации дифференциальных уравнений. Это означает, что после перехода в область изображений используются только алгебраические операции и находится изображение решения дифференциального уравнения, при этом автоматически учитываются начальные условия. Таким образом, решение дифференциального уравнения разбивается на два этапа: получение изображения решения и определение оригинала по изображению.

На первом этапе при алгебраизации дифференциального уравнения пользуются стандартными формулами:

Здесь через L обозначено применение к функции преобразования Лапласа, т.е. переход к изображению. Изображение функции в правой части дифференциального уравнения можно найти по таблицам, которые есть как в учебной литературе по математике, так и в литературе по теории управления 1.

На втором этапе определения оригинала по изображению в случае дробно-рациональной функции можно воспользоваться формулой на основе вычетов:

В этой формуле l-количество различных полюсов функции Y(s), k_i – кратность i–го полюса.

Другим способом является разложение изображения на простые слагаемые и нахождение по таблице оригинала каждого слагаемого. В случае вещественных кратных полюсов количество слагаемых равно кратности полюса, каждое слагаемое в знаменателе имеет сомножитель

В случае комплексных полюсов слагаемое должно быть приведено к табличному виду с помощью выделения полного квадрата:

Далее остается разложить на два слагаемых, чтобы в числителе были табличные выражения.

Видео:Годограф вектор функцииСкачать

Годограф скорости

ГОДОГРАФ СКОРОСТИ. Пусть точка перемещается по некоторой траектории АВ. В каждый момент времени вектор скорости (v) направлен по касательной к траектории в соответствующем положении точки, причем v = dr/dt, где r — радиус-вектор, определяющий положение точки на кривой по отношению к некоторой системе отсчета с произвольным началом О (фиг. 1). Вектор ускорения (а) равен производной вектора (v) по времени (t) а = dv/dt. Если от некоторой произвольной точки О₁ откладывать векторы h = v, то, при перемещении точки по своей траектории, вектор (h) будет менять в общем как свою абсолютную величину, так и направление, имея одно и то же начало О₁. Конец вектора (h) будет описывать кривую, называемую годографом скорости. Так как вектор (h) для кривой А₁В₁ играет ту же роль, что вектор (r) для кривой АВ, то скорость конечной точки вектора (h), при ее перемещении по А₁В₁, равна

Таким образом, видно, что вектор ускорения точки, движущейся по некоторой траектории, равняется в каждый момент соответствующему вектору скорости конца вектора, описывающего годограф скорости. Плоскость, касательная к годографу скорости и проходящая через (h), будет, очевидно, параллельна плоскости, проходящей через (а) и (v), т. е. она будет параллельна соприкасающейся плоскости кривой АВ.

При прямолинейном равномерном движении (v = Const) годограф скорости стягивается в одну точку. Если точка перемещается по кривой, имея одну и туже линейную скорость (v = Const), то годограф скорости представляет собой кривую, описанную на шаровой поверхности радиуса (v).

При плоском движении, годограф скорости — плоская кривая. Для свободной материальной точки, брошенной под углом к горизонту с некоторой начальной скоростью v₀, имеем: v = v₀ + gt, где v — вектор скорости точки по истечении времени (t), а g = Const — вектор ускорения силы тяжести. Так как h₀ = v₀ = Const, а вектор (gt) сохраняет постоянно вертикальное направление, то конец вектора (h = v) постоянно лежит на вертикали, т. е. годограф скорости для рассматриваемого случая представляет собой вертикальную прямую (фиг. 2).

Если точка описывает конического сечение с постоянной секториальной скоростью относительно фокуса конического сечения, то годограф скорости представляет собой окружность. Годограф скорости впервые был рассмотрен Гамильтоном, а затем Мёбиусом.

Источник: Мартенс. Техническая энциклопедия. Том 5 — 1929 г.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Построение годографа скоростей заданной точки

Годографом скоростей называется кривая, которая является геометрическим местом точек конца вектора скорости. Годограф позволяет определить скорость точки в любой момент времени по модулю и линии действия.

Годограф выгодно строить для точек, совершающих криволинейное движение. Для этого откладываем векторы скоростей соответствующей точки, полученные на планах скоростей, из общего полюса р в их истинном направлении и в одном масштабе. Соединяем концы всех векторов плавной кривой.

Для примера построим годограф скоростей точки К (точку К в механизме задаёт преподаватель). Пусть точка К делит звено АВ пополам. На всех двенадцати планах скоростей поделим векторы 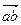пополам. Ставим точку k. Соединяем её с полюсом плана скоростей. Полученные векторы (скорость точки К в масштабе – ) переносим в общий полюс р. Рядом с концом каждого вектора необходимо указать номер соответствующего положения кривошипа механизма.

Соединяем концы векторов плавной кривой (рис. 15).

Рис. 15. Годограф скоростей точки К.

Определение угловых скоростей звеньев механизма

Угловые скорости звеньев можно определить, используя относительные скорости построенного плана скоростей.

Угловая скорость первого звена была определена выше и равна ω₁=3,14 рад/с.

Модуль угловой скорости звена 2 найдём по формуле:

(8)

Для определения направления ω₂ необходимо мысленно перенести вектор относительной скорости из плана скоростей в точку В плана механизма (рис. 16), при этом видим, что вектор скорости стремится вращать точку В звена АВ относительно точки А против часовой стрелки, следовательно, и угловая скорость второго звена ω₂ будет направлена против часовой стрелки (т.е. положительно).

Аналогично определяем модули и направления угловых скоростей остальных звеньев.

Угловая скорость звена 3 по модулю равна:

и направлена против часовой стрелки.

Угловая скорость звена 4 по модулю равна:

и направлена против часовой стрелки.

Результаты расчета запишем в таблицу 5.

Таблица 5. Относительные скорости точек и угловые скорости

звеньев для двенадцати положений механизма.

скорости № положения	относительные скорости точек, м/с	угловые скорости звеньев, рад/с
V_B_А		V_D_С	w₂	w₃	w₄
0, 12
0,390	0,410	0,220	0,700	0,976	0,314

Направление угловых скоростей звеньев указано на схеме механизма (рис 16).

Рис. 16. Схема механизма с указанием направлений относительных линейных скоростей точек и угловых скоростей звеньев.

Определение линейных ускорений точек

Звеньев механизма

Определение линейных ускорений точек звеньев механизма происходит в той же последовательности, что и определение линейных скоростей. Пример построения плана ускорений выполнен для положения 5 механизма (рис. 17).

Первой точкой, ускорение которой надо определить, является точка А ведущего звена. Так как кривошип 1 вращается с постоянной угловой скоростью, то абсолютное ускорение точки А определяется только величиной нормального ускорения, которое по модулю равно:

. (9)

Вектор направлен вдоль кривошипа O₁A от точки А к оси вращения О₁.

На плоскости выбираем произвольную точку q (полюс плана ускорений), которая является началом отсчета и ускорение которой равно нулю. Откладываем от неё вектор (параллельно звену O₁A в направлении от точки А к точке О₁).

Длина этого вектора изображает на плане ускорений вектор ускорения точки А и выбирается так, чтобы площадь плана ускорений была равна примерно 150 см 2 . Примем длину вектора равным 98 мм, тогда масштабный коэффициент плана ускорений будет:

(10)

Рассмотрим первую группу Ассура, образованную звеньями 2 и 3. Ускорения точек А и О₂ известны. Определим ускорение точки В.

Оно складывается из абсолютного ускорения точки А и относительного ускорения точки В при вращении звена 2 вокруг точки А.

С другой стороны точка В принадлежит звену 3, и ее ускорение складывается из ускорения точки O₂ и относительного ускорения точки В при вращении звена 3 вокруг точки O₂.

Составим систему двух векторных уравнений:

. (11)

Так как точка В движется криволинейно, то относительные ускорения представим в виде суммы двух ускорений: нормального и тангенциального.

. (12)

Абсолютные величины нормальных ускорений определяются по формуле:

, (13)

Вектор нормального ускорения направлен вдоль звена АВ от точки В к точке А (к оси вращения), а нормального ускорения — вдоль звена BO₂ от точки В к точке O₂ (к оси вращения). Тангенциальные составляющие ускорений и по абсолютной величине неизвестны, но известны их линии действия. Они направлены перпендикулярно к нормальным составляющим (или перпендикулярно к соответствующим звеньям).

В системе уравнений (12) нам известны: ускорение точки А, ускорение точки O₂ ( =0), , и линии действия и . Эта система уравнений может быть решена графическим методом.

Рис. 17. Пример построения плана ускорений.

Через точку а плана ускорений проводим прямую, направленную вдоль звена АВ, и на ней откладываем вектор в направлении от точки В к точке А:

величина которого в масштабе соответствует величине вектора нормальной составляющей ускорения .

Через точку n₁, перпендикулярно к звену АВ (или то же самое, что перпендикулярно ) проводим линию действия вектора тангенциального ускорения .

Рассмотрим второе уравнение системы (12). Из полюса q (точка O₂ совпадает с полюсом q, т.к. её ускорение равно нулю) проводим прямую, параллельную звену O₂B. В направлении от точки В к точке O₂ (на плане механизма) откладываем на этой прямой отрезок qn₂, который в масштабе равен модулю вектора нормального ускорения :

Через точку n₂ перпендикулярно к звену O₂B проводим линию действия вектора тангенциального ускорения . Пересечение двух прямых на плане ускорений, изображающих линии действия тангенциальных ускорений, дает точку b.

Соединяя точку b с полюсом плана ускорений q, получим вектор , соответствующий на плане вектору абсолютного ускорения точки В механизма, величина которого равна:

Из плана ускорений можно определить абсолютную величину тангенциальных составляющих относительных ускорений:

Вектор относительного ускорения на плане ускорений показан штриховой линией и равен:

а вектор совпадает по величине и линии действия с вектором абсолютного ускорения .

Для определения ускорения точки C воспользуемся свойством подобия. Величина отрезка qc может быть найдена из соотношения:

; отсюда: .

Величина абсолютного ускорения точки C механизма равна:

Рассмотрим вторую группу Ассура, образованную звеньями 4 и 5. Определим ускорение точки D. Шатун 4 совершает плоско – параллельное движение, ползун 5 – прямолинейное поступательное движение (частный случай плоскопараллельного движения). Таким образом, точка D одновременно совершает два движения: вращательное относительно точки C и поступательное относительно неподвижной стойки. Ускорение точки D΄, связанной с неподвижной направляющей ползуна равно нулю.

Система уравнений для ускорения точки D будет имеет вид:

. (14)

Относительное ускорение 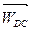представим в виде суммы двух составляющих — нормальной и тангенциальной.

. (15)

Величина нормального ускорения определяется по формуле:

Вектор нормального ускорения направлен вдоль звена CD от точки D к точке C (оси вращения). Тангенциальная составляющая по абсолютной величине неизвестна, но известна её линия действия. Она направлена перпендикулярно к нормальной составляющей. Вектор направлен вдоль направляющей.

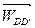
Система уравнений (12) имеет две неизвестные величины и решается графическим методом.

Через точку c плана ускорений проводим прямую, направленную вдоль звена CD в направлении от точки D к точке C, и на ней откладываем отрезок:

величина, которого в масштабе соответствует величине вектора нормальной составляющей ускорения .

Через точку n₃, перпендикулярно к звену CD (или то же самое, что перпендикулярно ) проводим линию действия вектора тангенциального ускорения . Рассмотрим второе уравнение системы (15). Из полюса q (т.к. ускорение D´=0 и совпадает с полюсом q) проводим прямую, параллельную направляющей ползуна х-х. Пересечение двух прямых на плане ускорений дает точку d. Полученный отрезок qd, соответствует на плане ускорений вектору абсолютного ускорения точки D механизма, величина которого равна:

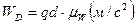
Из плана ускорений можно определить действительную величину тангенциальной составляющей относительного ускорения:

Вектор относительного ускорения шарниров звена на плане ускорений показан штриховой линией и равен:

Заполним таблицу 6.

Таблица 6. Относительные ускорения шарниров звеньев для

двух положений механизма, м/с 2 .

№ положе- ния ускорение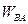
0,272	0,860	0,900	0,402	1,06	1,13	0,069	0,260	0,270

Определим ускорения центров тяжести звеньев S₂, S₃ и S₄ при помощи свойства подобия. Найдем положения точек центров тяжести на плане ускорения. Предположим, что центры тяжести s₂, s₃ и s₄ находятся посередине звеньев и делят векторы , , и пополам (рис.18). Центр тяжести ползуна 5 совпадает с точкой D, поэтому точка s₅ на плане скоростей совпадает с точкой d.

Рис. 18. Определение ускорений центров тяжести звеньев механизма

Соединим полученные точки s₂, s₃, s₄ и s₅ с полюсом q плана ускорений, тогда векторы , , и будут в масштабе изображать ускорение центра тяжести соответствующего звена.