Как определить большую сторону треугольника

Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.

Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.

a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.

Сумма углов треугольника равна 180°

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Величина большего угла треугольника не может быть меньшей, чем 60°.

,

где α – больший угол треугольника.

Величина меньшего угла треугольника не может быть большей, чем 60°.

,

где β – меньший угол треугольника.

,

Фигура	Рисунок	Формулировка
Треугольник
Большая сторона треугольника		Против большей стороны треугольника лежит больший угол
Больший угол треугольника		Против большего угла треугольника лежит большая сторона
Меньшая сторона треугольника		Против меньшей стороны треугольника лежит меньший угол
Меньший угол треугольника		Против меньшего угла треугольника лежит меньшая сторона
Длины сторон треугольника
		Углы треугольника
Внешний угол треугольника
Больший угол треугольника
Меньший угол треугольника
Теорема косинусов
Теорема синусов

Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.

Определение . Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.

a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.

Сумма углов треугольника равна 180°

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Величина большего угла треугольника не может быть меньшей, чем 60°.

,

где α – больший угол треугольника.

Величина меньшего угла треугольника не может быть большей, чем 60°.

,

где β – меньший угол треугольника.

,

Треугольник
Большая сторона треугольника
	Против большей стороны треугольника лежит больший угол
Больший угол треугольника
	Против большего угла треугольника лежит большая сторона
Меньшая сторона треугольника
	Против меньшей стороны треугольника лежит меньший угол
Меньший угол треугольника
	Против меньшего угла треугольника лежит меньшая сторона
Длины сторон треугольника
	Углы треугольника
Внешний угол треугольника
Больший угол треугольника
Меньший угол треугольника
Теорема косинусов
Теорема синусов

Треугольник

Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.

Определение . Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Большая сторона треугольника

Свойство большей стороны треугольника:

Против большей стороны треугольника лежит больший угол

Больший угол треугольника

Свойство большего угла треугольника:

Против большего угла треугольника лежит большая сторона

Меньшая сторона треугольника

Свойство меньшей стороны треугольника:

Против меньшей стороны треугольника лежит меньший угол

Меньший угол треугольника

Свойство меньшего угла треугольника:

Против меньшего угла треугольника лежит меньшая сторона

Длины сторон треугольника

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.

a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.

Углы треугольника

Свойство углов треугольника:

Сумма углов треугольника равна 180°

Внешний угол треугольника

Свойство внешнего угла треугольника:

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Больший угол треугольника

Свойство большего угла треугольника:

Величина большего угла треугольника не может быть меньшей, чем 60°.

,

где α – больший угол треугольника.

Меньший угол треугольника

Свойство меньшего угла треугольника:

Величина меньшего угла треугольника не может быть большей, чем 60°.

,

где β – меньший угол треугольника.

Теорема косинусов

Теорема синусов

Свойство меньшего угла треугольника:

,

Как найти сторону треугольника — в помощь школьнику

Есть несколько способов решения этой геометрической задачи. Они описаны в статье.

При помощи сторон и углов

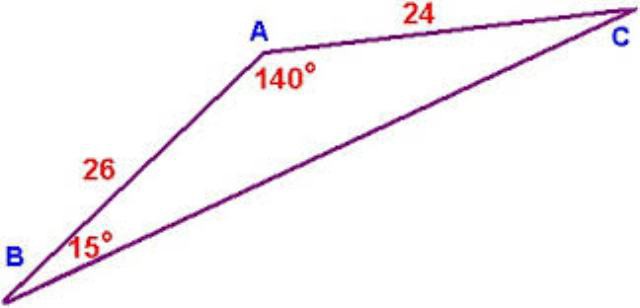
Итак, первый способ нахождения сторон треугольника — это по нескольким сторонам и углу между ними (и аналогично с углами и одной прилежащей стороной). Данный способ подойдет для старшей школы, так как здесь используются такие понятия, как синус, косинус, квадрат числа и корень. Итак, как найти сторону треугольника, который является произвольным? Для начала нарисуем эту самую фигуру. Теперь давайте обзовем элементы нашей фигуры. Стороны будут a, b и c. Угол, находящийся напротив стороны a, у нас будет «альфа», напротив b -«бета», напротив c — «гамма».

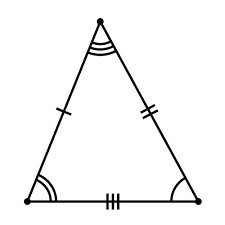
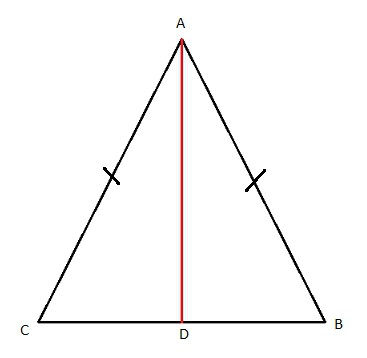
Равнобедренный треугольник

Что такое равнобедренный треугольник? Сам по себе он имеет две одинаковые стороны и так называемое основание. Стороны-близнецы обозначим буквой a, основание — b. Стало быть, раз у треугольника есть два «бедра» одной величины, то и углы на «фундаменте» тоже будут одинаковыми. Их назовем «альфа». Для того чтобы ответить, как найти сторону равнобедренного треугольника, необходимо ввести еще одну величину — угол, образованный между равными «бедрами».
Так как он располагается напротив b, то назвать его лучше всего «бета». Здесь при поиске неизвестных сторон можно пользоваться несколькими формулами. Давайте же посмотрим, какими именно. Первые две — это те, по которым можно вычислить длину стороны основания равнобедренного треугольника. Основана она на знаниях ученика о синусах и косинусах.

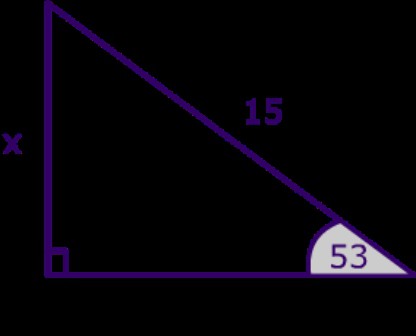
Прямоугольный треугольник

Наверное, каждый школьник, который только начал изучение геометрии, знает, что такое прямоугольный треугольник. С первого взгляда в данной фигуре нет ничего особенного, сложного и непонятного. Но вот когда «теряются» данные о той или иной стороне сего геометрического объекта, начинаются проблемы. Дело все в том, что вопрос: «Как найти сторону прямоугольного треугольника?» — затрагивает не только понятия синуса и косинуса, а еще и тангенсов углов. Таким образом, вычисления становятся намного сложнее и больше. Итак, сначала обозначим два катета нарисованного прямоугольного треугольника через a и b. Углы, лежащие напротив этих сторон, как и принято было прежде, назовем «альфа» и «бета» соответственно. Нашей гипотенузой будет служить сторона c. Угол, лежащий против него, нам не понадобится — он будет прямым. Вариантов вычислений тут несколько. Первый называется классическим. Для катета a формулы выглядит как: a=c*cos»бета»=c*sin»альфа»=b*tg»альфа».

Итоги

Итак, сегодня мы разобрались, как найти сторону треугольника, и выучили много новых формул. Для того чтобы лучше их запомнить, запишите их на какую-нибудь бумажку, по которой потом будет проще учить все наизусть. Не стоит пугаться «страшных» цифр и больших вычислений. Все проще, чем кажется.

Треугольник. Формулы и свойства треугольников.

Типы треугольников

По величине углов

По числу равных сторон

Вершины углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

если α > β , тогда a > b

если α = β , тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

a + b > c
b + c > a
c + a > b

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

a	=	b	=	c	= 2R
sin α		sin β		sin γ

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 — 2 bc · cos α

b 2 = a 2 + c 2 — 2 ac · cos β

c 2 = a 2 + b 2 — 2 ab · cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β

b = a cos γ + c cos α

c = a cos β + b cos α

Формулы для вычисления длин сторон треугольника

Медианы треугольника

Свойства медиан треугольника:

В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

Медиана треугольника делит треугольник на две равновеликие части

Треугольник делится тремя медианами на шесть равновеликих треугольников.

Формулы медиан треугольника

Формулы медиан треугольника через стороны

m_a = 1 2 √ 2 b 2 +2 c 2 — a 2

m_b = 1 2 √ 2 a 2 +2 c 2 — b 2

m_c = 1 2 √ 2 a 2 +2 b 2 — c 2

Биссектрисы треугольника

Свойства биссектрис треугольника:

Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны:

l_a = 2√ bcp ( p — a ) b + c

l_b = 2√ acp ( p — b ) a + c

l_c = 2√ abp ( p — c ) a + b

где p = a + b + c 2 — полупериметр треугольника

Формулы биссектрис треугольника через две стороны и угол:

l_a = 2 bc cos α 2 b + c

l_b = 2 ac cos β 2 a + c

l_c = 2 ab cos γ 2 a + b

Высоты треугольника

Свойства высот треугольника

Формулы высот треугольника

h_a = b sin γ = c sin β

h_b = c sin α = a sin γ

h_c = a sin β = b sin α

Окружность вписанная в треугольник

Свойства окружности вписанной в треугольник

Формулы радиуса окружности вписанной в треугольник

r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )

Окружность описанная вокруг треугольника

Свойства окружности описанной вокруг треугольника

Формулы радиуса окружности описанной вокруг треугольника

R = S 2 sin α sin β sin γ

R = a 2 sin α = b 2 sin β = c 2 sin γ

Связь между вписанной и описанной окружностями треугольника

Средняя линия треугольника

Свойства средней линии треугольника

MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC

MN || AC KN || AB KM || BC

Периметр треугольника

Периметр треугольника ∆ ABC равен сумме длин его сторон

Формулы площади треугольника

Формула Герона

S =	a · b · с
	4R

Равенство треугольников

Признаки равенства треугольников

Первый признак равенства треугольников — по двум сторонам и углу между ними

Второй признак равенства треугольников — по стороне и двум прилежащим углам

Третий признак равенства треугольников — по трем сторонам

Подобие треугольников

∆MNK => α = α ₁, β = β ₁, γ = γ ₁ и AB MN = BC NK = AC MK = k ,

где k — коэффициент подобия

Признаки подобия треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

📸 Видео