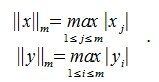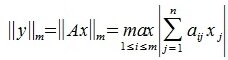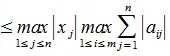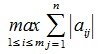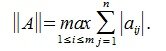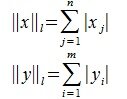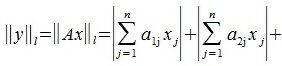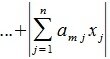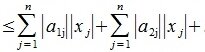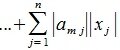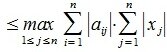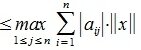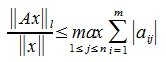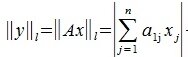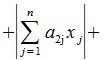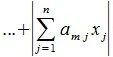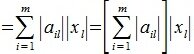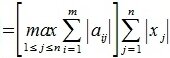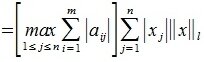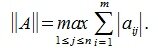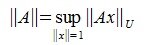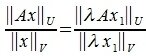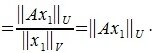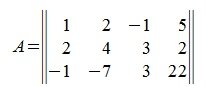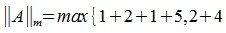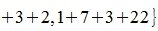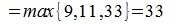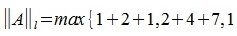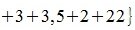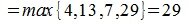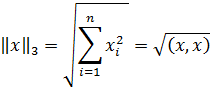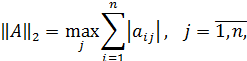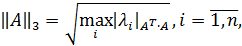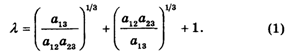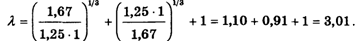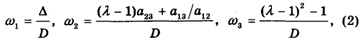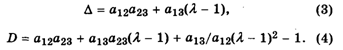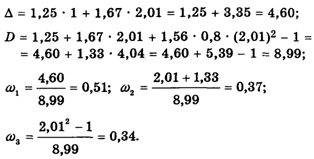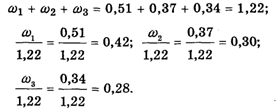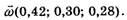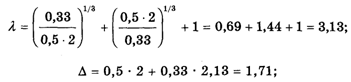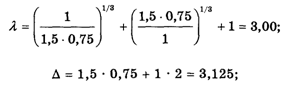Как нормировать вектор матрицы (5 видео)

Норма матрицы

Рассмотрим произвольную матрицу A порядка m×n и связанную с нею линейное преобразование y=Ax, где x∈V n , y∈U m . Введем в этих пространствах нормы векторов , .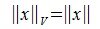

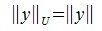
Определим норму матрицы A равенством:

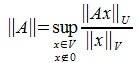(1)

Из определения нормы матрицы следует:

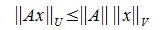(2)

Пусть для двух матриц A и B порядка m×n определены одни и те же векторные нормы. Тогда имеем соотношение:

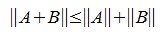(3)

Кроме того справедливо равенство

где λ любое число.

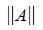
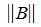
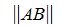
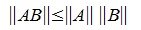
Пусть для m×n матрицы A и n×k матрицы B определены матричные нормы , и пусть для m×k матрицы AB определена норма . Тогда

Вычислим норму матрицы A , введя в пространствах V и U конкретные векторные нормы.

1. Пусть в пространствах V и U введена векторная норма

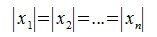
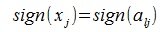
В (5) и (6) неравнетство превращается в равенство, если взять и , j=1. n, где l-то значение i, при котором

достигает своего максимума. Учитывая высшеизложенное, неравенство (6) и равенство (1), получим:

2. Введем в пространствах V и U векторную норму

Пусть 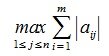достигается при j=l. Для вектора x, у которого только один элемент отлично от нуля, имеем:

Учитывая (1),(8) и (9) получим l-норму матрицы A:

Норму матрицы, определяемую с помощью формулы (1), называется операторной нормой, подчиненной данной норме векторов.

Отметим, что определение нормы матрицы (1) эквивалентно следующему определению:

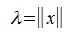
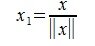
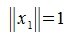
Действительно, любой ненулевой вектор x∈V можно представить в виде произведения λx₁, где , . Тогда, учитывая, что , получим:

Содержание

Примеры вычисления нормы матрицы
Геометрическая интерпретация нормы матрицы
Нормы векторов и матриц
9.3. Метод собственного вектора
📹 Видео

Видео:Орт вектора. Нормировать вектор. Найти единичный векторСкачать

Примеры вычисления нормы матрицы

Вычислим m-норму и l-норму матрицы используя (7) и (10).

Видео:Матрицы и векторыСкачать

Геометрическая интерпретация нормы матрицы

Пусть в линейном пространстве V введена m-норма для всех векторов x∈V:

Найдем норму матрицы

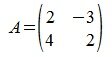
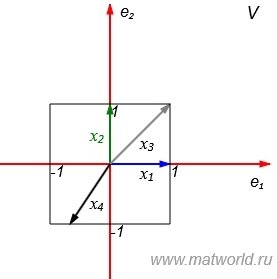
Рассмотрим множество всех векторов, которые имеют норму 1. В двухмерном пространстве это те векторы конечные точки которых находятся на квадрате на рис. 1. Обозначим это множество символом X₀.

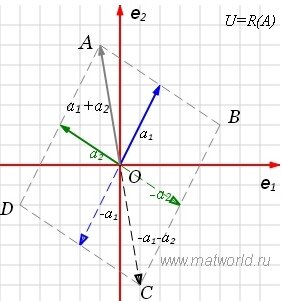
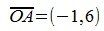
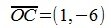
На рисунке рис. 2 изображено пространство столбцов матрицы A. Каждому вектору x∈X₀ соответствует вектор Ax в U. Конечные точки этих векторов находятся на пунктирном четырехугольнике ABCD. m-норма матрицы A — это модуль наибольшго координата наибольшего из векторов, конечная точка которого находится на четырехугольнике ABCD. На рис.2 это векторы и а модуль наибольшего координата 6. Используя (3), аналитически получим тот же результат.

Отметим, что норма матрицы показывает насколько максимально растягивается вектор x при отображении y=Ax. В нашем примере векторы х растягиваются максимально 6 раз.

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Нормы векторов и матриц

Для исследования сходимости и точности численных итерационных методов решения задач линейной и нелинейной и нелинейной алгебры, в том числе итерационных методов решения СЛАУ и СНАУ, необходимо ввести понятие нормы векторов матриц.

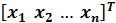
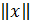
Нормой вектора х = (обозначают )

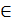
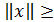
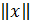
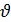
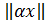
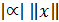
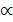
В n — мерной вещественном пространстве векторов x R n называют неотрицательное число, вычисляемое с помощью компонент вектора и обладающее следующими свойствами

а) 0 ( = 0 тогда и только тогда, когда x – нулевой вектор, т.е. x = );

б) = для любых чисел (действительных или комплексных);

в) .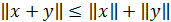

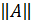
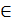
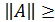
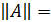
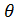
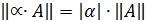
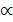
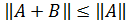
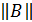
Нормой матрицы А_n₊_n(обозначается c вещественными элементами в n-мерном пространстве матриц А R n называют неотрицательное число, вычисляемое с помощью элементов матрицы и обладающее следующими свойствами:

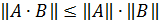
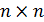
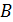
а) 0 ( 0 тогда и только тогда, когда А – нулевая матрица, т.е. А= );

б) для любых действительных и комплексных чисел ;

в) + ;

г) для всех матриц А и рассматриваемого пространства.

Нормы матриц и векторов, на которые матрицы действуют должны быть согласованы.

Норма матрицы А называется согласованной с нормой вектора х, на который действует матрица А; если выполняется неравенство

∙ , (*)

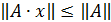
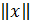
которое называется связью, осуществляющей согласование матрицы А с вектором х.

Наиболее употребительными являются следующие нормы векторов:

, I = , …

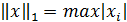
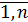
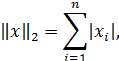
Согласованными с ними с помощью связи нормами матриц будут соответственно:

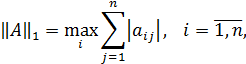
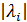
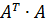
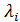
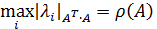
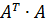
Где — модули собственных чисел симметрической вещественной матрицы для которой все являются действительными числами;

— максимальное по модулю собственное значение матрицы или спектральный радиус вещественной матрицы А.

Основная и дополнительная литература по дисциплине.

Основная:

1. Формалев В.Ф., Ревизников Д.Л. Численные методы.-М.: Физматлит 2004-400с.

2. Пирумов У.Г. (редактор). Численные методы. Учебник и практикум. Бакалавр. Академический курс.-М.: Юрайт, 2014-422с.

3. Численные методы. Сборник задач. Под редакцией У.Г.Пирумова.-М.: Дрофа, 2007-144с.

Дополнительная:

4. Вержбицкий В.М. Численные методы. Три книги:

1) Линейная алгебра и нелинейные уравнения.

2) Математический анализ и ЛДУ.

3) Дифференциальные уравнения в частных производных.

5. Демидович Б.П., Марон И.А. Основы вычислительной математики.-М.: наука, 1966, — 664с.

Учебная литература к лекции 1:

, с.3…15; ,с.3…6.

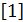
Дата добавления: 2016-03-04 ; просмотров: 1974 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Лекция 2, Векторные и матричные нормы, унитарные матрицы, SVDСкачать

9.3. Метод собственного вектора

Математические методы позволяют эффективно анализировать весьма сложные и большие системы, модели которых состоят из нескольких уровней. Например, известная модель мировой динамики Форрестера и Медоуза рассматривает ресурсы, население, уровень жизни, капиталовложения, загрязнение среды. Анализ состояния окружающей среды приводит к модели, уровнями которой могут быть: 1) типы загрязнителей SO2, NO4, CO2, CO, стоки вод, твердые отходы, земля), 2) способы очистки, 3) очистительные устройства. Изучение вопроса об общем благосостоянии страны целесообразно проводить по таким уровням: 1) экономика, оборона, здравоохранение; 2) отрасли промышленности; 3) ресурсы; 4) демография. Уровни располагаются по их значимости, т. е. образуют Иерархию. Анализ таких Иерархических систем, сводится прежде всего к тому, чтобы для каждого уровня выбрать Приоритеты и в соответствии с ними расположить объекты этого уровня. Основная цель анализа: выяснить, насколько влияют факторы самого низкого уровня на общую цель. Покажем на конкретном примере, как это делают Методом собственного вектора. Этот метод позволяет расположить рассматриваемые объекты по степени их значимости путем попарного сравнения по различным независимым признакам.

На должность юриста крупного предприятия претендуют трое (обозначим их А, В, С). Директор предприятия в большом затруднении, т. к. среди претендентов нет такого, кто превосходил бы остальных по всем параметрам. Один имеет больший опыт, зато другой имеет лучшее образование и опубликовал несколько научных работ; третий известен своей исключительной ответственностью и добросовестностью и т. д. Как выбрать Наилучшего по совокупности качеств? Тут директор вспомнил, что в институте экологии и права, где он учился, им преподавали математику, и, в частности, рассказывали о применении математических методов в теории принятия решений. Покопавшись в своих архивах, директор нашел лекции по математике и решил воспользоваться методом собственных векторов, применяемом при изучении иерархических систем.

Во-первых, он выбрал 3 основных критерия, по которым будут сравниваться кандидаты: профессионализм и опыт (критерий К1), ответственность и добросовестность (К2), организаторские способности (K3). По такому важному критерию как честность и порядочность претендентов сравнить было невозможно — у всех троих в характеристиках было написано по этому поводу практически одно и то же. Первая задача состояла в том, чтобы расположить эти критерии в порядке важности. Вторая задача состояла в том, чтобы сравнить кандидатов между собой по каждому из этих критериев, приписав каждому из них определенный балл.

Этап первый: сравнение критериев.

Исходя из своего жизненного и профессионального опыта, директор полагал, что критерий К1 важнее, чем критерии К2 и К3, причем, если сравнивать их количественно, в баллах, то К1 : К2

5 : 3. При этом, если, сравнивать последние два качества между собой, то они примерно равноценны, т. е. можно считать, что K2 : K3

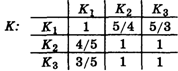
1 : 1. Далее директор составил матрицу К Размером 3´3, т. е. таблицу с тремя строками и тремя столбцами, куда занес отношения указанных баллов:

Число, стоящее на пересечении строки с номером I и столбца с номером J, обычно обозначают АIj. Поэтому у нас A11 = 1, A22 = 1, А33 = 1, A12 = 5/4, A13 = 5/3, А23 = 1, и т. д. Заметьте, что числа Aij и АJi являются взаимно обратными.

Все дальнейшие вычисления будем проводить вместе с директором приближенно, округляя до сотых долей, причем нам понадобятся только числа А12 = 1,25; A13 = 1,67 и A23 = 1.

Прежде всего находят так называемое Главное собственное число L матрицы К по формуле

Пользуясь калькулятором, получаем:

Теперь находим координаты W1, W2 и W3 так называемого Главного собственного вектора матрицы К по формулам

Подставляя сюда наши значения А12 = 1,25; A13 = 1,67;

A23 = 1, последовательно получаем:

Теперь собственный вектор 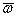(W1, W2, W3) Нужно Нормировать, т. е. каждую координату разделить на сумму всех координат. Имеем:

Сумма полученных чисел равна единице. Обозначим вектор, координатами которого являются эти числа, также буквой :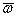

Этот вектор называется Вектором приоритетов. Согласно теории, качества К1, К2 и K3 можно расположить по приоритету с баллами 0,42; 0,30 и 0,28 соответственно.

Этап второй: сравнение претендентов по качеству К1. Из имеющихся у него документов (характеристик, рекомендаций, отзывов, научных публикаций) директор сумел сравнить между собой каждую пару претендентов по качеству К1. У него получилось А : В

1 : 2 (т. е. у В Балл в 2 раза выше, чем у А), А : С

2 : 1. Поэтому матрица К1 попарных сравнений получилась такая

Из нее видно, что А12 = 0,5, А13 = 0,33, А23 = 2. Подставляя эти числа в формулы (1)-(4), как и в предыдущем случае находим:

Итак, в этом случае вектор приоритетов будет 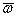(0,17; 0,48; 0,35), т. е., если сравнивать, претендентов по качеству К1, то они получают баллы 0,17, 0,48 и 0,35 соответственно.

Этап третий: сравнение претендентов по качеству K2:

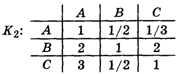
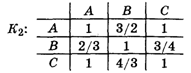
Как было видно из документов, каждые двое из претендентов работали некоторое время в одной и той же фирме и вели примерно одинаковые дела. Просмотрев последние и оценив качество исполнения, директор получил следующие отношения при попарном сравнении по критерию K2: А : В

3 : 4. Запишем матрицу К2 попарных сравнений:

Вектор приоритетов будет 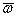(0,38; 0,26; 0,36), так что по качеству К2 претенденты получают баллы 0,38, 0,26 и 0,36 соответственно.

Этап четвертый: сравнение по качеству K3. Поскольку никто из претендентов прежде не находился на руководящей работе, то директор, исходя из весьма туманных соображений и своей интуиции, смог только оценить вероятность того, что тот или иной претендент станет хорошим руководителем. Получились вероятности 0,8, 0,7 и 0,6 соответственно. Таким образом, удалось обойтись без попарного сравнения. 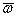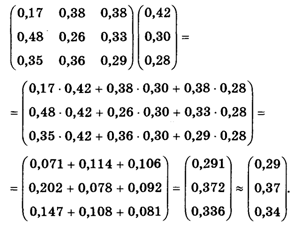Разделив каждое из указанных чисел на их сумму 0,8 + 0,7 + 0,6 = 2,1, находим вектор приоритетов: (0,38; 0,33; 0,29).

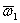
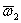
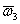
Этап пятый: получение окончательно результата. Согласно теории, окончательное распределение мест получается следующим образом. Составим из векторов , и матрицу 3´3, записав их координаты в столбцы:

Затем умножим эту матрицу на матрицу-столбец

Составленную из координат вектора 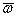. По правилу умножения матриц,

Итак, окончательное распределение мест следующее:

Претендент А набрал 0,29 балла, претендент В — 0,37 балла, претендент C — 0,34 балла. Метод собственного вектора отдал предпочтение претенденту В.

Предупреждение: не попадайте под гипнотическое воздействие чисел! Несмотря на объективность математических методов, полученный результат нельзя рассматривать как истину в последней инстанции. Хотя бы потому, что выбор исходного материала (т. е. чисел А12, а13 и А23, входящих в матрицы К1, К2, К3), был в значительной степени субъективным. Поэтому и претендент С, имеющий примерно такой же балл, как и В, Также имеет шанс на успех, в особенности, если он не курит или согласен на меньшую зарплату.

1. Описанным методом можно сравнивать любое число кандидатов и по любому числу критериев, однако при большом их числе придется пользоваться другими формулами, приведенными, например, в книге Т. Саати «Принятие решений».

2. Вычислительные трудности, разумеется, можно переложить на ЭВМ.

3. Мы сознательно упростили ситуацию, опустив некоторые тонкости, связанные с оценкой метода. О них также можно прочитать в книге Т. Саати.

4. Еще раз отметим, в чем сила описанного метода. Сравнить каждые два объекта между собой по одному критерию довольно просто, и это дает возможность сравнительно легко заполнить матрицу попарных сравнений. Но затем, с помощью несложных вычислений, мы находим ответ уже на довольно трудный вопрос: какой из рассматриваемых объектов превосходит остальные по совокупности всех критериев.

Метод собственного вектора можно применять для анализа самых разнообразных проблем, о которых шла речь в начале параграфа. Например, автор упомянутой выше книги проанализировал этим методом рост терроризма для агентства по контролю над вооружениями и разоружением в Вашингтоне.

В качестве самостоятельной задачи попробуйте оценить претендентов на должность мэра Вашего города, выбрав критерии по своему усмотрению.