Найти центр окружности при помощи треугольника и карандаша

Друзья, по техническим причинам я вынужден заранее выложить задачу следующей недели.

На предстоящей неделе вам предстоит найти центр круга с помощью чертежного треугольника и карандаша.

Вам дан круг произвольного радиуса. Задача – имея в собственном распоряжении только чертежный треугольник и карандаш, определить, где находится центр круга.

Мы ждем ваши сканы, фотографии и чертежы, выполненные вами в данной ветке форума.

• 142 просмотра

У меня получилось так

Поду рукой не было треугольника, поэтому начертил в автокаде. Но суть остается неизменной.

1)Проводим касательную к окружности.

2)Проводим касательную к окружности, которая перпендикулярна касательной из 1).

3)Проводим касательную к окружности, которая перпендикулярна касательной из 2).

4)Проводим касательную к окружности, которая перпендикулярна касательной из 3).

Получаем квадрат и проводим в нем две диагонали. Точка пересечения диагоналей — центр окружности. (Получился четурехугольник(квадрат) описанный над окружностью.

Метод №2.
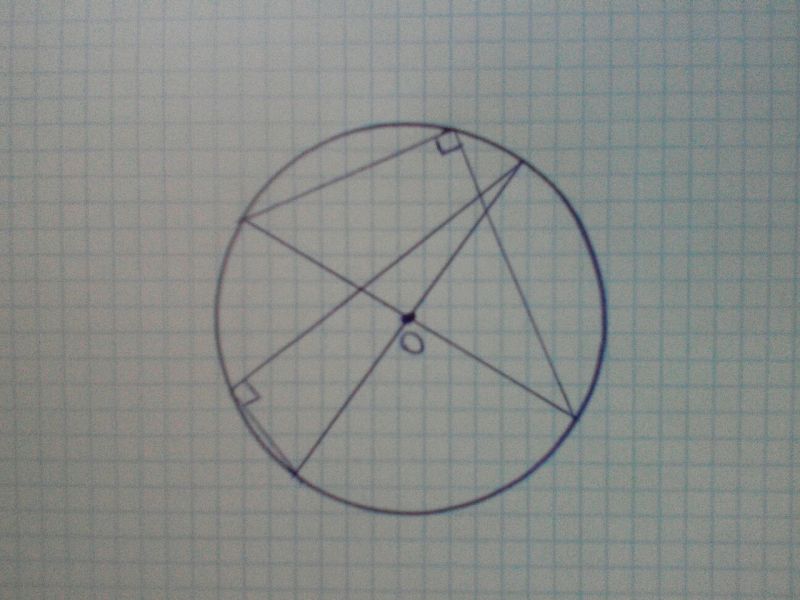
Вписанный угол равен половине дуги =>с помощью треугольника чертим два прямоугольных треугольника, у которых гипотенузы будут диаметрами окружности. Точка пересечения — искомый центр. =)

Видео:Как найти центр круга в мастерской (4 способа)Скачать

Как найти центр окружности с помощью треугольника

Видео:Быстро и легко определяем центр любой окружностиСкачать

Найти центр окружности используя треугольник

Видео:Не каждый знает как найти центр окружности без циркуля! #ShortsСкачать

Как найти центр круга?

Как найти центр окружности при помощи чертежного треугольника без делений и карандаша?

Видео:Как найти центр и радиус нарисованной окружности #математика #егэ2023 #школа #fyp #shortsСкачать

Ответ

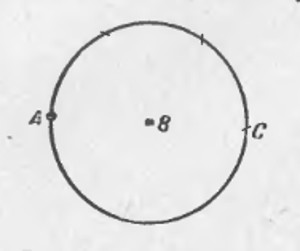
Накладываем чертежный (прямоугольный) треугольник на окружность так, чтобы вершина С треугольника совместилась с какой-нибудь точкой окружности, и отмечаем точки D и Е пересечения катетов с окружностью. Поскольку у прямоугольного треугольника центр описаной окружности лежит на середине гипотенузы, отрезок DE будет диаметром окружности. Аналогичным путем построим второй диаметр. Точка пересечения двух диаметров и будет центром окружности.

Видео:Возьми на заметку! Как быстро найти центр окружности.#shortsСкачать

О задаче

• Категория: Геометрические задачи,
• Степень сложности: средняя.
• Ключевые слова: карандаш, круг, окружность, треугольник, центр,
• Источник: Математическая смекалка, Сборник задач по математике на сообразительность,

Видео:Геометрия Задача найти центр круга /math and magicСкачать

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

Видео:Как найти центр круга с помощью подручных средств? ЛЕГКО.Скачать

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Решите задачу

На рисунке изображены две одинаковые монеты, одна под другой. Представьте себе, что верхняя монета катится по краю нижней и вновь возвращается на прежнее место. Сколько раз она обернется при этом вокруг своего центра?

Видео:4K Как найти центр окружности, how to find the center of a circleСкачать

Занимательные задачи

Ещё больше занимательных задач собрано в следующих разделах:

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Быстрый способ, как найти центр окружности

В данном обзоре автор поделится с нами довольно простым способом, как быстро найти центр окружности.

Для этого нам потребуется всего два предмета: угольник и карандаш. Первым делом необходимо провести прямую линию в любом месте окружности.

Советуем также прочитать: как изготовить своими руками антенну для усиления 4G сигнала на даче или в частном доме.

После того, как начертили линию, измеряем длину, и делим это расстояние ровно пополам.

В данном случае длина линии составляет 210 мм. Разделив ее пополам, получаем 105 мм — ставим в этом месте отметку.

С помощью угольника проводим вторую линию, которая должна быть перпендикулярна первой (то есть проходить под углом 90 градусов).

Видео:Как найти центр окружности с помощью циркуля и линейкиСкачать

Основные этапы работ

На следующем этапе проделываем те же операции с другой стороны окружности (только не параллельно, а немного в стороне).

Чертим линию, измеряем ее длину (в данном случае — 218 мм), делим пополам (109 мм) и откладываем в этом месте точку. После этого проводим перпендикулярную линию, как и в предыдущем случае.

Пересечение двух линий, которые мы чертили под углом 90 градусов, и будет являться центром круга.

Подробно об этом способе можно посмотреть на видео ниже. Статья подготовлена на основе видео с YouTube канала « ПОГРАНЕЦ 13 ».

Видео:Радиус описанной окружностиСкачать

Исследовательская работа по математике: «Как определить центр окружности»

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №1 с. Александров – Гай

Исследовательская работа по математике:

Подготовил: Амиров Марат, ученик 6 «а»

класса МБОУ СОШ №1 с. Александров – Гай

Руководитель: , учитель математики МБОУ СОШ №1 с. Александров — Гай

С. Александров – Гай

Глава 1 «Способы нахождения окружности» …………………………………..4

Глава 2 «Практическая часть»…………………………………………………..6

Список литературы и источников………………………………………………12

Окружность — совокупность точек, находящихся на равном расстоянии от одной точки, называемой центром. Однако в тех случаях, когда вам дана одна только окружность, нахождение ее центра может быть непростой задачей. Поэтому цель моей исследовательской работы: изучить способы определения центра окружности. Исходя из цели были поставлены задачи:

— найти самый простой способ определения центра окружности;

— сравнить несколько способов определения центра окружности;

— практические способы определения центра окружности.

Актуальность ислледовательской работы заключается в том, что в повседневной жизни людей часто приходится находить центр окружности, но не каждый знает как это правильно сделать. Поэтому изучение данной темы поможет найти правильное решение проблемы и определить оптимальный вариант для человека любой професии.

При написании исследовательской работы были использованны электронные источники и литература. Электронные источники помогли найти теоретический материал по теме, а учебники по математике были использованны для подбора задач и практической части работы.

Глава 1. Способы нахождения центра окружности.

1.Самый простой способ нахождения центра окружности — согнуть лист бумаги, на котором она начерчена, следя на просвет, чтобы окружность оказалась сложена точно пополам. Полученная линия сгиба будет одним из диаметров заданной окружности. Затем лист можно согнуть в другом направлении, получив тем самым второй диаметр. Точка их пересечения и будет центром окружности.

2. Для того чтобы найти центр окружности, надо сначала вписать ее в квадрат. То есть все стороны четырехугольника должны касаться круга. Для этого проведите с помощью линейки четыре ровные линии. Теперь соедините по диагонали два противоположных угла. Следите за тем, чтобы линия разбивала угол квадрата на две равные части. Соедините прямыми все 4 угла квадрата. Точка пересечения данных прямых и будет центром окружности.

3. Для любого треугольника центр описанной окружности находится в точке пересечения срединных перпендикуляров. Если этот треугольник — прямоугольный, то центр описанной окружности всегда совпадает с серединой гипотенузы. Следовательно, если вписать в окружность прямоугольный треугольник, то его гипотенуза будет диаметром этой окружности.
В качестве трафарета для этого способа подойдет любой прямой угол — школьный или строительный угольник, или просто лист бумаги. Поместите вершину прямого угла в любую точку окружности и сделайте отметки там, где стороны угла пересекают границу круга. Это конечные точки диаметра.
Тем же способом найдите второй диаметр. В точке их пересечения

4.На круглую деталь накладываем лист бумаги так, что бы один его угол находился на окружности или крае круга. И отмечаем точки, где лист соприкасается другими краями с кругом. Отмечаем эти точки.

Проводим прямую линию между отмеченными точками. Расстояние между ними является диаметром этого круга. Обрезаем лишнюю бумагу и проводим на детали прямую линию — диаметр.

Достаточно переместить наш треугольник в другое положение и нарисовать еще один диаметр круга, как тут же в точке пересечения диаметров мы и получим искомый центр окружности…

5. Диаметр и радиус окружности.

Диаметр окружности — это отрезок прямой, соединяющий пару наиболее удаленных друг от друга точек окружности, проходящий через центр окружности. Слово «диаметр» произошло от греческого слова «diametros» — поперечный. Обычно диаметр обозначается латинской буквой D или значком Ø.

Диаметр можно найти по формуле: D = 2R, где диаметр равен удвоенному радиусу окружности.
Радиус — расстояние от центра до любой точки окружности. Обозначается латинской R.
Если известен радиус окружности, допустим, он равен 8 см, то значит D = 2 * 8 = 16 см.

Радиус окружности определяется по формуле : R=D:2

» width=»390″ height=»299 >
Глава 2 «Практическая часть»

1) Прямой угол детали закруглен дугой радиуса R

Для решения задачи с центром в вершине прямого угла проводят окружность радиуса R, которая пересекает стороны прямого угла в точках А и В.

С центрами в точках А и В строят еще две окружности радиуса R; С – их точка пересечения. Дуга окружности радиуса R с центром в точке С и будет искомым закруглением.

Произвольный угол детали закруглить дугой радиуса R

Решение: На расстоянии R от сторон угла проводят соответствующие параллельные им прямые. О — их пересечение. Затем строим окружность с центром О, радиуса R

Даны две параллельные прямые и точка А между ними. Как построить окружность, касающуюся данных прямых и проходящих через данную точку?

1) Построим любую окружность, касающуюся двух прямых (центр окружности находим, разделив ее пополам)

2) Проведем через А прямую, равную данным. Она пересечет построенную окружность в точках В и С. Перед ними центр построенной окружности на АВ или АС.

Задачи на построение технического рисунка

Как при помощи слесарного разметочного угольника измерить недоступный диаметр круглой детали.

Можно ли прибором, изображенным на рисунке одним прикладыванием найти центр круга?

«Как найти центр окружности?» — вопрос, на который мне пришлось ответить в ходе исследования. Таким образом, я нашел несколько способов построения центра окружности: 1) центроискатель — прямой угол. Принцип работы: вписанный угол опирается на диаметр. 2) Центроискатель — угол с биссектрисой. Принцип работы: диаметр окружности лежит на биссектрисе угла, описанного около этой окружности.3)Центроискатель – пара взаимно перпендикулярных прямых. Принцип работы: диаметр, проведенный в точку касания, перпендикулярен касательной. 4)Центроискатель – пара взаимно перпендикулярных прямых. Принцип работы: хорда, перпендикулярная другой хорде и проходящая через ее середину, есть диаметр.

Соответственно цель моей работы достигнута: изучив несколько способов нахождения центра окружности возможно из каждого выбрать оптимальный вариант.

О, математика земная!
Гордись, прекрасная, собой,
Ты всем наукам мать родная,
И дорожат они тобой.

Твои расчеты величаво
Ведут к планетам корабли
Не ради праздничной забавы,
А ради гордости Земли!

Список использованной литературы и источников

1.Журнал «Математика в школе» №20 1989г.

Видео:Построить описанную окружность (Задача 1)Скачать

Как найти центр круга?

Как найти центр окружности при помощи чертежного треугольника без делений и карандаша?

Видео:Как найти центр кругаСкачать

Ответ

Накладываем чертежный (прямоугольный) треугольник на окружность так, чтобы вершина С треугольника совместилась с какой-нибудь точкой окружности, и отмечаем точки D и Е пересечения катетов с окружностью. Поскольку у прямоугольного треугольника центр описаной окружности лежит на середине гипотенузы, отрезок DE будет диаметром окружности. Аналогичным путем построим второй диаметр. Точка пересечения двух диаметров и будет центром окружности.

Видео:Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

О задаче

• Категория: Геометрические задачи,
• Степень сложности: средняя.
• Ключевые слова: карандаш, круг, окружность, треугольник, центр,
• Источник: Математическая смекалка, Сборник задач по математике на сообразительность,

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Видео:Как найти центр кругаСкачать

Решите задачу

Сколько трехзначных чисел можно составить с помощью трех цифр 1, 2 и 3 так, чтобы одна и та же цифра встречалась в каждом числе не больше одного раза?

Видео:КАК БЫСТРО НАЙТИ ЦЕНТР КРУГАСкачать

Занимательные задачи

Ещё больше занимательных задач собрано в следующих разделах:

Видео:Как легко найти центр окружности?Скачать

Планиметрия (прямая и окружность)

Планиметрия изучется в начальном курсе геометрии и зачастую сводится к решению практических задач без изучения теоретической базы.
В данной статье приводятся альтернативные (подсказкам) решения задач из первого раздела (кроме 1.5) приложения Euclidea (геометрические построения с помощью циркуля и линейки).

Решения задач 1.1, 1.2 и 1.3 основаны на том, что с помощью циркуля и линейки можно построить равносторонний треугольник.

1.1 Построить угол 60° с заданой стороной

1.2 Построить серединный перпендикуляр к отрезку

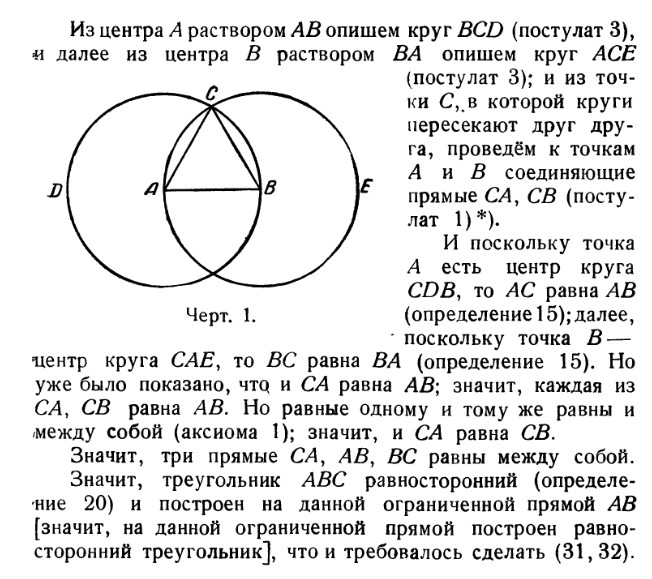
На данной ограниченной прямой построить равносторонний треугольник

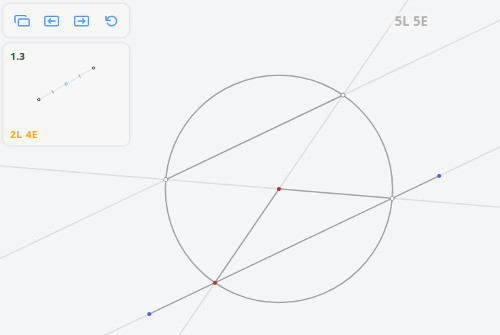
1.3 Середина отрезка

всё, что можно построить с помощью циркуля и линейки, может быть построено с помощью одного циркуля.

Из точки В радиусом АВ описываем окружность.
По этой окружности откладываем от точки А расстояние АВ три раза: получаем точку С, очевидно, диаметрально противоположную А. Расстояние АС представляет собой двойное рассрастояние АВ. Проведя окружность из С радиусом ВС, мы можем таким же образом найти точку,
диаметрально противоположную В и, следовательно, удаленную от А на
тройное расстояние АВ, и т. д.

любое построение, выполнимое на плоскости циркулем и линейкой, можно выполнить одной линейкой, если нарисована хотя бы одна окружность и отмечен её центр.

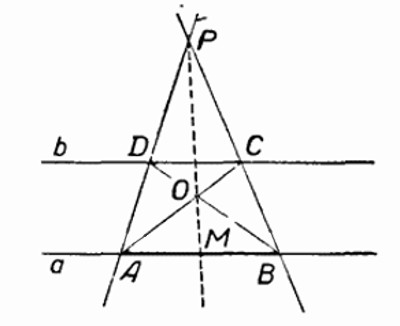
Проведем прямые PA и PB и отметим точки D и C их пересечения прямой b. Пусть О — точка пересечения прямых AC и BD. Тогда, согласно предыдущей лемме, прямая PO пересечёт отрезок AB в его середине M.

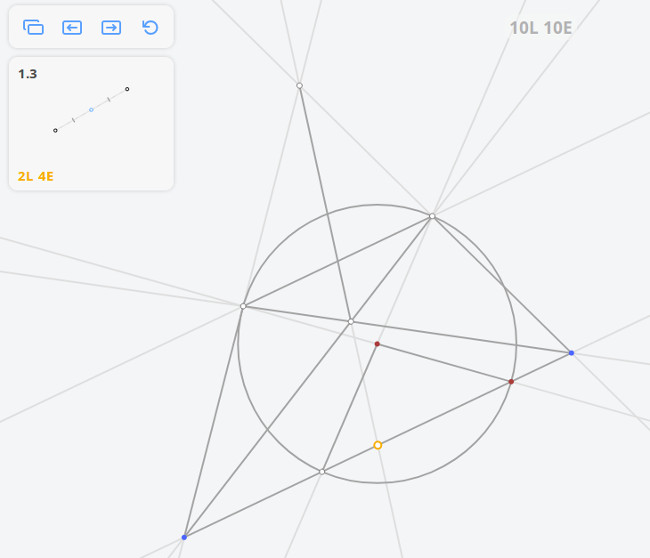
Решением задачи 1.3 по методу Штейнера-Понеселе будет:

1.4 Окружность, вписанная в квадрат

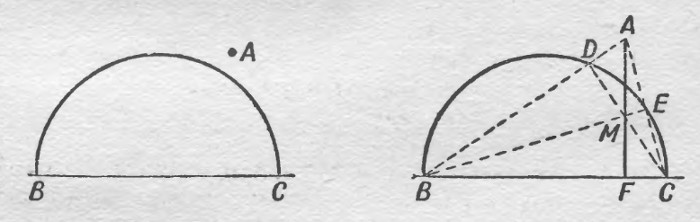
Из точки A, лежащей вне данной полуокружности, опустить на её диаметр перпендикуляр, обходясь при этом без циркуля. Положение центра полуокружности не указано.

Нам пригодится здесь то свойство треугольника, что все его высоты пересекаются в одной точке. Соединим A с B и C; получим точки D и E. Прямые BE и CD, очевидно, — высоты треугольника ABC. Третья высота — искомый перпендикуляр к BC — должна проходить через пересечение двух других, т.е. через точку M. Проведя по линейке прямую через точки A и M, мы выполним требованиек задачи, не прибегая к услугам циркуля.

И опустив перпендикуляр из точки пересечения диагоналей квадрата на ребро, найдём середину ребра.
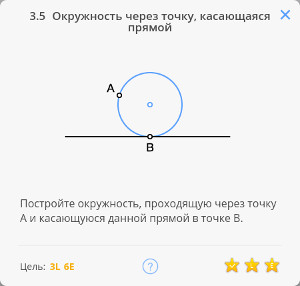
Это же построение можно использовать для решения задачи 2.9 Окружность, касающаяся прямой

1.6 Найти центр окружности

Плоский угол, опирающийся на диаметр окружности, — прямой.

Определение: касательной к окружности называется прямая, имеющая с окружностью одну общую точку. Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.

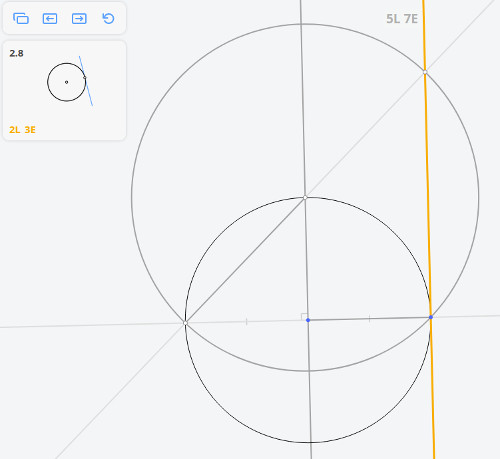
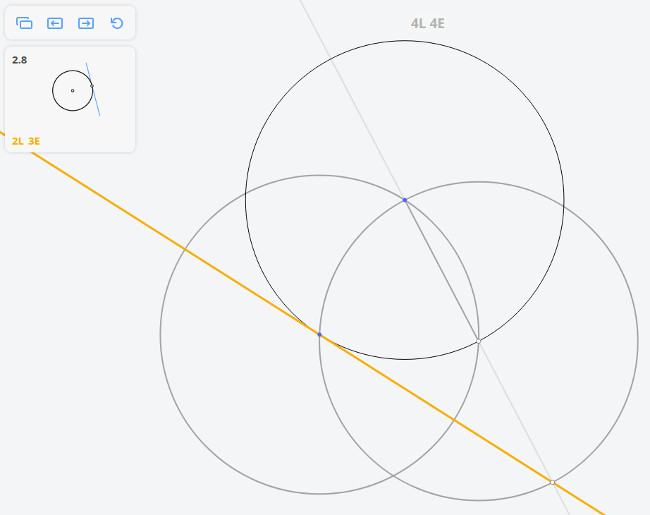
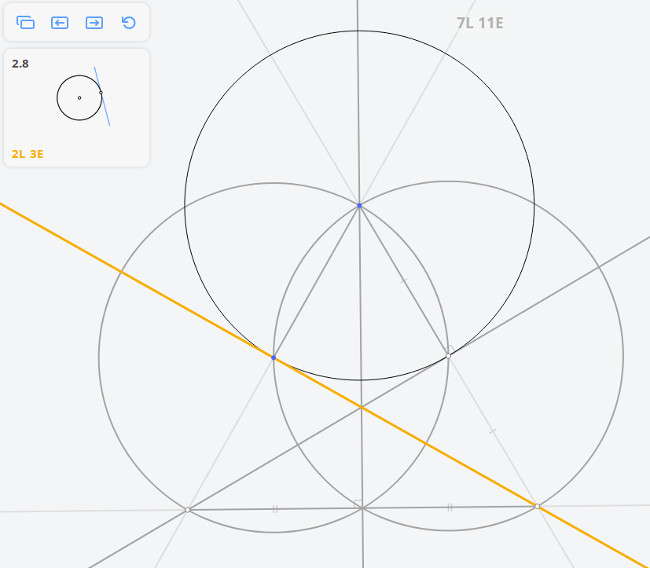
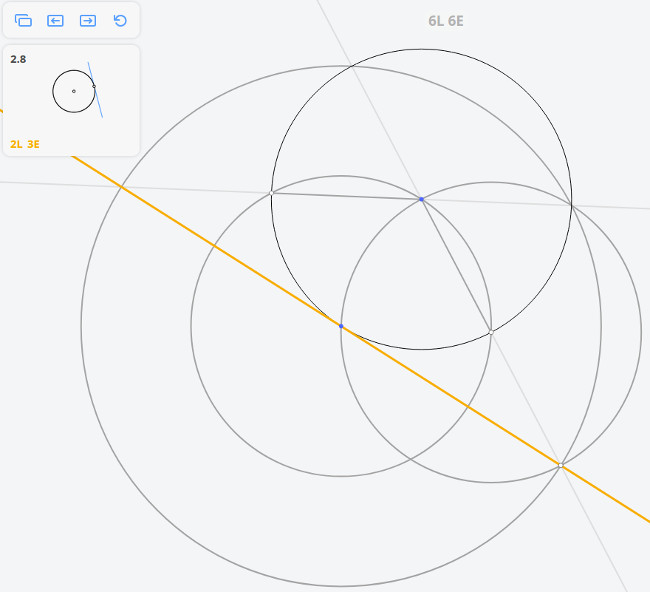
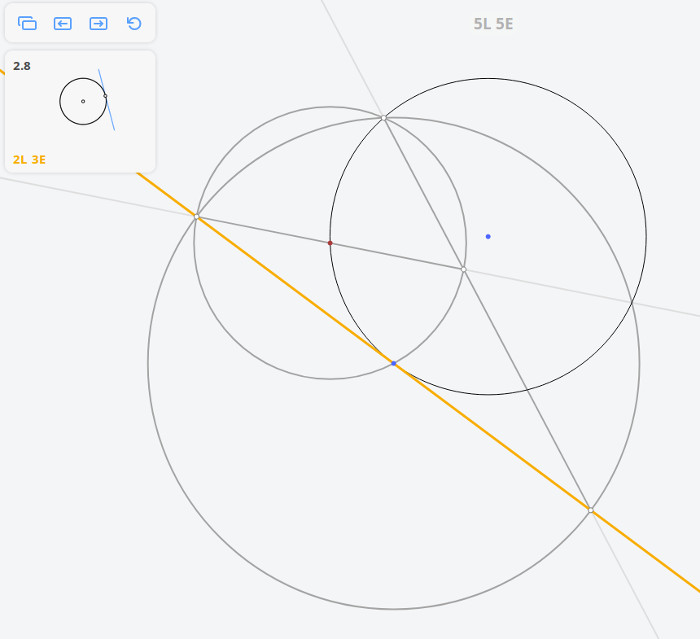
Рассмотрим задачу 2.8
2.8 Касательная к окружности в точке
Возвращаясь к предыдущей задаче, эту задачу можно решить построив угол, опирающийся на диаметр окружности по теореме Фалеса

Далее, построив перпендикуляр к касательной, найдём диаметр окружности, и, разделив его пополам, найдём центр окружности.

Ещё об одном способе построения касательной к окружности можно узнать из лекции 1.5 курса «Геометрия и группы» А. Савватеева ссылка

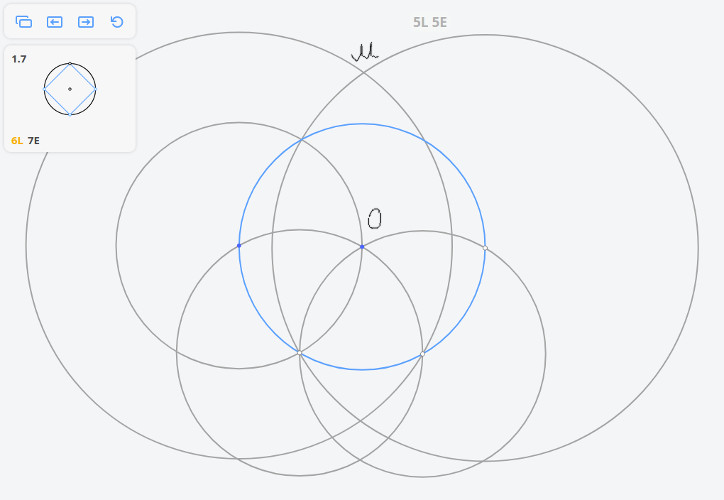
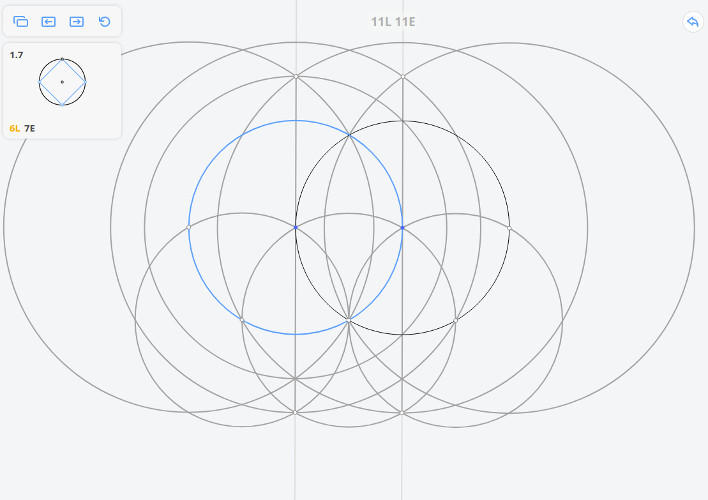
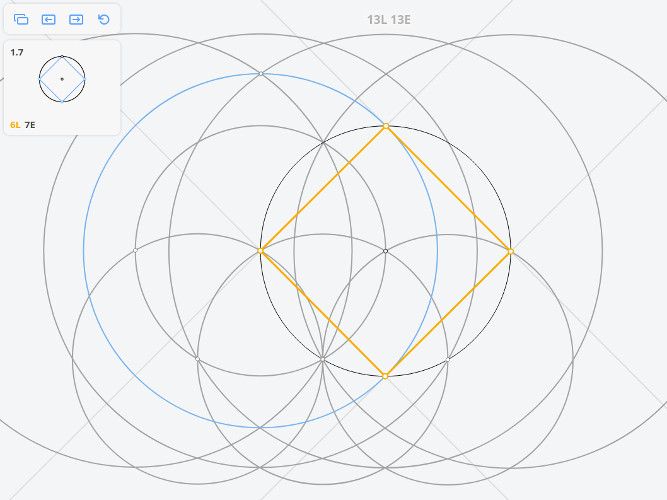
1.7 Квадрат, вписанный в окружность

Задача Наполеона

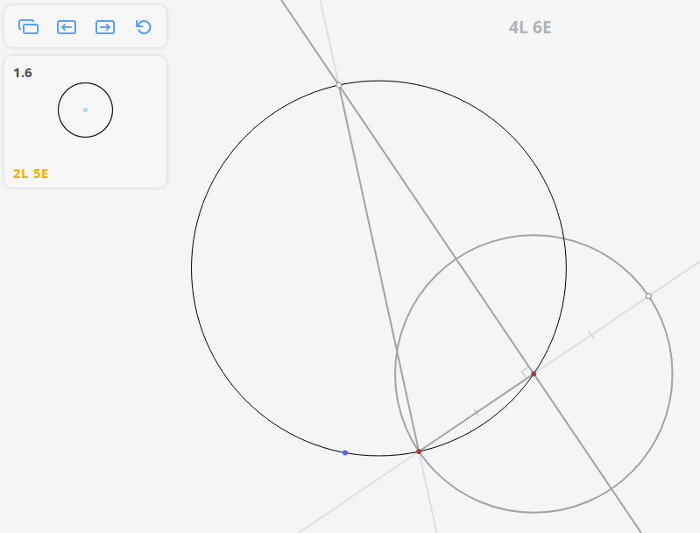
Решим задачу методом Мора-Маскерони.
Построим три окружности радиусом r и две окружности радиусом

В приложении нет такой операции, как перенос раствора циркуля (равного MO), поэтому необходимо использовать дополнительные построения.
Для того, чтобы построить касательную к исходной окружности, параллельную МО, необходимо произвести построения, которые были приведены выше (построить три окружности радиусом r и две окружности радиусом ), но вместо исходной окружности взять окружность, обозначенную на рисунке синим цветом

Т.о. мы перенесли раствор циркуля (равный МО) в точку А.
Далее из точки А необходимо провести окружность c радиусом МО

Как найти центр окружности?

Как найти центр окружности при помощи чертежного треугольника без делений и карандаша?

Ответ

Накладываем чертежный (прямоугольный) треугольник на окружность так, чтобы вершина С треугольника совместилась с какой-нибудь точкой окружности, и отмечаем точки D и Е пересечения катетов с окружностью. Поскольку у прямоугольного треугольника центр описаной окружности лежит на середине гипотенузы, отрезок DE будет диаметром окружности. Аналогичным путем построим второй диаметр. Точка пересечения двух диаметров и будет центром окружности.

О задаче

• Категория: Геометрические задачи,
• Степень сложности: средняя.
• Ключевые слова: карандаш, круг, окружность, треугольник, центр,
• Источник: Математическая смекалка, Сборник задач по математике на сообразительность,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Решите задачу

Сколько раз можно вычесть 6 из 30?

Занимательные задачи

Ещё больше занимательных задач собрано в следующих разделах: