Как называется правило сложения двух неколлинеарных векторов правило параллельных прямых

Отрезок, который имеет направление, называется вектором. По сути, эта линия, характеризующаяся определённой длиной. Так как с математической точки зрения это выражение, то с ним можно выполнять различные операции. Простейшими являются действия вычитания двух и более векторов и их сложение. Выполняются они по правилам геометрии и алгебры.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Общие сведения

Понятие вектор используется как в физике, так и в математике. С его помощью обозначают действие различных сил, указывают их направление, определяют движение. По сути, это величина, противопоставляемая массе, объёму, плотности, температуре, то есть «скалярам». Согласно определению вектор — это отрезок, имеющий строгое направление. Точку, из которой он выходит, называют начальной, а в которой заканчивается — конечной.

Обозначают отрезок помощью заглавных латинских букв, сверху которых ставится чёрточка. Рисуют же его с помощью прямой ограниченной линии.

Например, запись AB обозначает, что точка A является началом, а B концом. В некоторых случаях для кратности отрезки допустимо обозначать одной маленькой буквой, так: AB = a.

Векторная запись используется тогда, когда невозможно величины описать с помощью одного числа. Численное значение выражение определяется длиной отрезка или его модулем. Эта величина является скалярной. В том случае если начало и конец ограниченной линии совпадают, то говорят о нулевой линии. Обозначают её цифрой 0.

Векторы, расположенные на плоскости или в пространстве, по отношению друг к другу могут быть:

• коллинеарными — отрезки лежат на одной линии или ей параллельны;
• соноправленными — замкнутые линии направление которых одинаковое;
• противоположными — вектора направлены в разные стороны;
• ортогональными — перпендикулярными друг другу;
• компланарными — лежащими на одной плоскости или ей параллельные;
• равными — ограниченными прямыми, совпадающими как по направлению, так и по величине.

Так как вектора — это выражения, то с ними можно выполнять различные действия. Их возможно складывать, вычитать, умножать на число. При работе с векторными величинами используют декартовую систему координат. В ней прямую замкнутую линию раскладывают по базису и определяют координаты её точек. Другими словами, выполняют проекции отрезков на оси. Непосредственно за базис берут орты.

Если известны начальные координаты и конечные, то текущие вычисляют путём вычитания из последних первые. Существующая возможность записать любое геометрическое свойство, используя координаты, позволяет отойти от геометрии и использовать для вычислений алгебру.

Видео:8 класс, 44 урок, Законы сложения векторов. Правило параллелограммаСкачать

Сложение координат

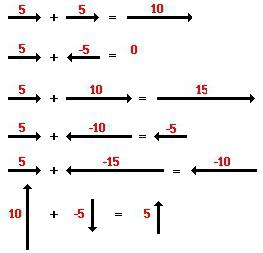
Существует простое правило применимое для направленных отрезков и позволяющее найти их сумму. Заключается оно в следующем: если необходимо прибавить один вектор к другому описывающийся каждый своими координатами, достаточно сложить соответствующие их орты. Например, предположим есть два вектора a и b. Первый отрезок имеет координаты (ax; ay), а второй (bx;by). При их сложении получится новый вектор c. В результате действия его координаты будут c (ax + bx; ay + by).

Это теорема доказывается просто. Пусть даны отрезки f (x 1; y 1) и g (x 2; y 2). В системе координат относительно рассматриваемых векторов получится: f = x 1 a + y 1 b; g = x 2 a + y 2 b. Тогда искомая сумма будет: f + g = x1a + y1b + x2a + y2b = a (x 1 + x 2) + b (y 1 + y 2). Что и нужно было доказать. Это правило применимо к векторам имеющим любые координаты. Например, пусть есть a (1; 2), b (-3; 1). Нужно найти их сумму. С помощью формулы сложения получится новый направленный отрезок с координатами a + b = (1 — 3; 2 + 1) = (-2; 3).

Как и при операциях с простыми числами при работе с векторными выражениями используют различные их свойства. Существует три правила сложения векторов:

Приведённые свойства соответственно называют переместительным, сочетательным, нулевым законом. Например, предположим есть два направленных отрезка a (2; 2) и b (-4; 1). Согласно первому свойству, очерёдность значения не имеет, поэтому что при прибавлении b к a, что при a к b результат будет одинаковый: a + b = (2 -4; 2 + 1) = (-2; 3), b + a = (-4 + 2; 1 +2) = (-2; 3). По аналогии можно проверить правильность утверждения и двух оставшихся свойств.

Следует отметить, что при сложении двух противоположных ограниченных прямых сумма будет равняться нуль-вектору: a + (-a) = 0. Это утверждение не требует доказательства, так как здесь используется фундаментальный закон алгебры — правило знаков.

Видео:Сложение векторов. Правило параллелограмма. 9 класс.Скачать

Правило параллелограмма

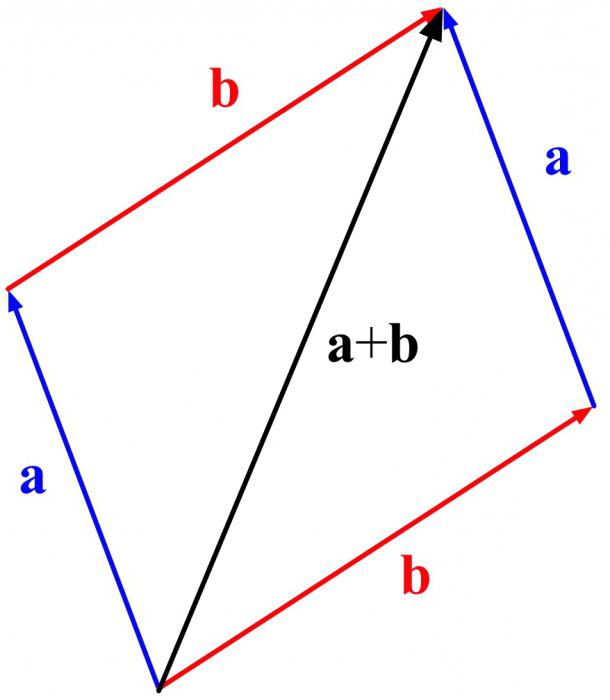
По сути, все операции с векторными выражениями сводятся к их приращению или уменьшению. Если координаты точек неизвестны, то алгебраический метод складывания не подходит. В таком случае используют геометрические операции. Одним из способов, позволяющих сложить два неколлинеарных вектора, является правило параллелограмма или прямоугольника при перпендикулярном направлении складываемых отрезков.

Сформулировать способ можно следующим образом: если имеются два отрезка не лежащие на параллельной прямой и не принадлежащие ей, то нужно достроить данные вектора до параллелограмма. Для этого необходимо взять произвольную точку и отложить от неё отрезок AB равный первому вектору, и AD совпадающий со вторым. При этом необходимо придерживаться соотношения геометрии наклона. Затем достроить необходимые параллельные прямые таким образом, чтобы образовался параллелограмм ABCD. Если в такой фигуре провести диагональ, то её длина и будет равняться сумме складываемых отрезков.

Доказать правильность утверждения можно следующими доводами. Пусть имеются две ограниченные линии a и b. От точки A можно отложить первый отрезок конец, которого обозначить как B, и второй, с точкой D. Теперь через D и B возможно провести соответственно параллельные прямые AB и AD. Место, в которой они пересекутся, пусть будет обозначено как С. Тогда используя признак параллельности двух пар прямых в фигуре ABCD, можно утверждать, что это параллелограмм. Вектор AC = a + b. Это следует из равенства отрезков AD = BC и теоремы о подобных треугольниках.

Пример задания. Определить, чему равна сумма двух отрезков длиной 2 см и 1 см расположенные друг к другу под углом 45. Для того чтобы воспользоваться правилом, нужно взять листочек в клеточку и построить два вектора, исходящие из одной точки O. Тогда первый отрезок будет OA, а второй OB. Затем достроить прямые таким образом, чтобы на рисунке получился параллелограмм. Новая полученная точка пусть будет D. Теперь с помощью линейки можно измерить диагональ фигуры, длина которой и будет искомой суммой. В ответе должно получиться, что OA + OB = OD = 3 см.

Простыми словами это правило можно рассказать так: сумма двух отрезков будет равняться диагонали параллелограмма, построенного на исходных векторах. Эта теорема чаще используется не в геометрии, а физике, например, при сложении сил.

Видео:Геометрия 9 класс (Урок№2 - Сумма двух векторов. Законы сложения векторов.)Скачать

Альтернативные методы

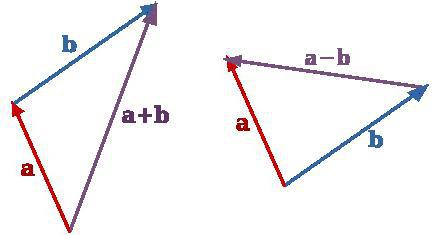
Операцию по сложению двух векторов можно выполнить и с помощью правила треугольника. Делается это так. Выбирается любая точка на плоскости, от которой откладываются два вектора. При этом необходимо соблюдать их размерность и наклон по отношению друг к другу. Затем две конечные точки соединяют прямой. Её длина и будет искомой величиной. То есть в итоге должна получиться равнобедренная фигура.

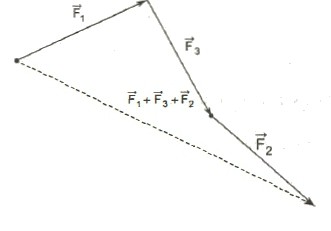
Применение метода сложения векторов по правилу треугольника позволяет довольно легко находить сумму для трёх и более отрезков. Для этого сначала вычисляют результат сложения для двух любых линий, а после прибавляют к полученной ограниченной прямой третью и так далее.

При сложении нескольких векторов удобно выполнять следующую последовательность построений:

• от выбранной точки пространства рисуется вектор, равняющийся первому слагаемому;
• от конечной точки откладывается вектор, совпадающий со вторым слагаемым;
• приведённая последовательность потеряется необходимое число раз;
• прямой линией соединяется точка, с которой началось построение с конечной последнего вектора;
• длина полученного отрезка и будет являться результатом сложения.

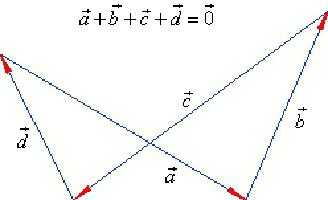
Этот способ получил название метод многоугольника. Он довольно часто применяется на практике, позволяя, довольно просто выполнить нахождение суммы. Из правила треугольника, а, следовательно, и многоугольника, вытекает следствие, которое подтверждает, что если складывается отрезок с нулевым векторным выражением, то в ответе получится длина, совпадающая со значимым слагаемым.

Следует отметить, что методы используются только, если направление отрезков является сонаправленным.

Если же отрезки неколлинеарные, то от конца одного откладывается другой. Тогда искомая сумма будет равняться длине линии, первой точкой которой будет начало одной векторной прямой, а конец совпадать с точкой, завершающей другую. То есть сумма — это отрезок, начало которого совпадает с началом обеих линий, а длина равна разности их длин, при этом направление его будет совпадать с тем что больше по длине.

Видео:Сложение векторов. 9 класс.Скачать

Правила, по которым происходит сложение векторов

Как происходит сложение векторов, не всегда понятно ученикам. Дети не представляют того, что за ними скрывается. Приходится просто запоминать правила, а не вдумываться в суть. Поэтому именно о принципах сложения и вычитания векторных величин требуется много знаний.

В результате сложения двух и более векторов всегда получается еще один. Причем он всегда обязательно будет одинаковым, независимо от приема его нахождения.

Чаще всего в школьном курсе геометрии рассматривается сложение двух векторов. Оно может быть выполнено по правилу треугольника или параллелограмма. Эти рисунки выглядят по-разному, но результат от действия один.

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Как происходит сложение по правилу треугольника?

Оно применяется тогда, когда векторы неколлинеарные. То есть не лежат на одной прямой или на параллельных.

В этом случае от некоторой произвольной точки нужно отложить первый вектор. Из его конца требуется провести параллельный и равный второму. Результатом станет вектор, исходящий из начала первого и завершающийся в конце второго. Рисунок напоминает треугольник. Отсюда и название правила.

Если векторы коллинеарные, то это правило тоже можно применять. Только рисунок будет расположен вдоль одной линии.

Видео:№741. Начертите два неколлинеарных вектора а и b. Изобразите несколько векторов:Скачать

Как выполняется сложение по правилу параллелограмма?

Опять же? применяется только для неколлинеарных векторов. Построение выполняется по другому принципу. Хотя начало такое же. Нужно отложить первый вектор. И от его начала — второй. На их основе достроить параллелограмм и провести диагональ из начала обоих векторов. Она и будет результатом. Так выполняется сложение векторов по правилу параллелограмма.

До сих пор их было два. А как быть, если их 3 или 10? Использовать следующий прием.

Видео:83. Законы сложения векторов. Правило параллелограммаСкачать

Как и когда применяется правило многоугольника?

Если требуется выполнить сложение векторов, число которых — больше двух, пугаться не стоит. Достаточно последовательно отложить их все и соединить начало цепочки с ее концом. Этот вектор и будет искомой суммой.

Видео:Разложение вектора на неколлинеарные вектора.Скачать

Какие свойства действительны для действий с векторами?

О нулевом векторе. Которое утверждает, что при сложении с ним получается исходный.

О противоположном векторе. То есть о таком, который имеет противоположное направление и равное по модулю значение. Их сумма будет равна нулю.

О коммутативности сложения. То, что известно еще с начальной школы. Смена мест слагаемых не приводит к изменению результата. Другими словами, неважно какой вектор откладывать сначала. Ответ все равно будет верным и единственным.

Об ассоциативности сложения. Этот закон позволяет складывать попарно любые векторы из тройки и к ним прибавлять третий. Если записать это с помощью знаков, то получится следующее:

первый + (второй + третий) = второй + (первый + третий) = третий + (первый + второй).

Видео:Правило рук 👋 КАК ЛЕГКО определять НАПРАВЛЕНИЕ ЛИНИЙ МАГНИТНОГО ПОЛЯ??Скачать

Что известно о разности векторов?

Отдельной операции вычитания не существует. Это связано с тем, что оно, по сути, является сложением. Только второму из них задается противоположное направление. А потом все выполняется так, как если бы рассматривалось сложение векторов. Поэтому об их разности практически не говорят.

Для того чтобы упростить работу с их вычитанием, видоизменено правило треугольника. Теперь (при вычитании) второй вектор нужно отложить из начала первого. Ответом будет тот, что соединяет конечную точку уменьшаемого с ней же вычитаемого. Хотя можно и откладывать так, как было описано ранее, просто изменив направление второго.

Видео:Вычитание векторов. 9 класс.Скачать

Как найти сумму и разность векторов в координатах?

В задаче даны координаты векторов и требуется узнать их значения для итогового. При этом построений выполнять не нужно. То есть можно воспользоваться несложными формулами, которые описывают правило сложения векторов. Они выглядят так:

а (х, у, z) + в (k, l, m) = с (х+k, y+l, z+m);

а (х, у, z) -в (k, l, m) = с (х-k, y-l, z-m).

Легко заметить, что координаты нужно просто сложить или вычесть в зависимости от конкретного задания.

Видео:Вектор. Определение. Коллинеарные векторы. Равные векторы.Скачать

Первый пример с решением

Условие. Дан прямоугольник АВСД. Его стороны равны 6 и 8 см. Точка пересечения диагоналей обозначена буквой О. Требуется вычислить разность векторов АО и ВО.

Решение. Сначала нужно изобразить эти векторы. Они направлены от вершин прямоугольника к точке пересечения диагоналей.

Если внимательно посмотреть на чертеж, то можно увидеть, что векторы уже совмещены так, чтобы второй из них соприкасался с концом первого. Вот только его направление неверное. Он должен из этой точки начинаться. Это если векторы складываются, а в задаче — вычитание. Стоп. Это действие означает, что нужно прибавить противоположно направленный вектор. Значит, ВО нужно заменить на ОВ. И получится, что два вектора уже образовали пару сторон из правила треугольника. Поэтому результат от их сложения, то есть искомая разность, — вектор АВ.

А он совпадает со стороной прямоугольника. Для того чтобы записать числовой ответ, потребуется следующее. Начертить прямоугольник вдоль так, чтобы большая сторона шла горизонтально. Нумерацию вершин начинать с левой нижней и идти против часовой стрелки. Тогда длина вектора АВ будет равна 8 см.

Ответ. Разность АО и ВО равна 8 см.

Видео:9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

Второй пример и его подробное решение

Условие. У ромба АВСД диагонали равны 12 и 16 см. Точка их пересечения обозначена буквой О. Вычислите длину вектора, образованного разностью векторов АО и ВО.

Решение. Пусть обозначение вершин ромба будет таким же, как в предыдущей задаче. Аналогично решению первого примера получается, что искомая разность равна вектору АВ. А его длина неизвестна. Решение задачи свелось к тому, чтобы вычислить одну из сторон ромба.

Для этой цели потребуется рассмотреть треугольник АВО. Он прямоугольный, потому что диагонали ромба пересекаются под углом в 90 градусов. А его катеты равны половинам диагоналей. То есть 6 и 8 см. Искомая в задаче сторона совпадает с гипотенузой в этом треугольнике.

Для ее нахождения потребуется теорема Пифагора. Квадрат гипотенузы будет равен сумме чисел 6 2 и 8 2 . После возведения в квадрат получатся значения: 36 и 64. Их сумма — 100. Отсюда следует, что гипотенуза равна 10 см.

Ответ. Разность векторов АО и ВО составляет 10 см.

Видео:Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Третий пример с детальным решением

Условие. Вычислить разность и сумму двух векторов. Известны их координаты: у первого — 1 и 2, у второго — 4 и 8.

Решение. Для нахождения суммы потребуется сложить попарно первые и вторые координаты. Результатом будут числа 5 и 10. Ответом будет вектор с координатами (5; 10).

Для разности нужно выполнить вычитание координат. После выполнения этого действия получатся числа -3 и -6. Они и будут координатами искомого вектора.

Ответ. Сумма векторов — (5; 10), их разность — (-3; -6).

Видео:10 класс, 43 урок, Компланарные векторыСкачать

Четвертый пример

Условие. Длина вектора АВ равна 6 см, ВС — 8 см. Второй отложен от конца первого под углом в 90 градусов. Вычислить: а) разность модулей векторов ВА и ВС и модуль разности ВА и ВС; б) сумму этих же модулей и модуль суммы.

Решение: а) Длины векторов уже даны в задаче. Поэтому вычислить их разность не составит труда. 6 — 8 = -2. Несколько сложнее обстоит дело с модулем разности. Сначала нужно узнать, какой вектор будет являться результатом вычитания. Для этой цели следует отложить вектор ВА, который направлен в противоположную сторону АВ. Потом от его конца провести вектор ВС, направив его в сторону, противоположную исходному. Результатом вычитания получится вектор СА. Его модуль можно вычислить по теореме Пифагора. Несложные вычисления приводят к значению 10 см.

б) Сумма модулей векторов получается равной 14 см. Для поиска второго ответа потребуется некоторое преобразование. Вектор ВА противоположно направлен тому, который дан — АВ. Оба вектора направлены из одной точки. В этой ситуации можно использовать правило параллелограмма. Результатом сложения будет диагональ, причем не просто параллелограмма, а прямоугольника. Его диагонали равны, значит, модуль суммы такой же, как в предыдущем пункте.

Видео:Сложение двух векторовСкачать

Тест с ответами: “Векторные величины”

1. Какое правило используется для сложения двух неколлинеарных векторов?
а) Правило Пифагора
б) Правило параллельных прямых
в) Правило параллелограмма +

2. Если два ненулевых вектора лежат на параллельных прямых или на одной прямой, то они называются:
а) сонаправленные
б) коллинеарные +
в) нулевые

3. Отрезок, для которого указано, какая из его граничных точек – начало, а какая – конец это:
а) Прямая
б) Луч
в) Вектор +

4. Выберите векторную физическую величину:
а) время
б) скорость тела +
в) масса тела

5. Нескольких векторов сложили по правилу многоугольника. Начало первого вектора совпало с концом последнего. Чему равна сумма векторов?
а) нулевому вектору +
б) вектору равному разнице первого вектора и последнего
в) единичному вектору

6. Как называются векторы, если они сонаправленные и имеют равные модули?
а) нулевые
б) Коллинеарные
г) Равные +

7. Чем характеризуются векторные величины?
а) численным значением и направлением +
б) только численным значением
в) только направлением

8. Два вектора коллинеарны и направлены в противоположные стороны. Их модули равны 3 и 4 соответственно. Чему равен модуль суммы этих векторов?
а) 1 +
б) 5
в) 7

9. Если из произвольной точки отложить первый вектор, из конца полученного вектора отложить второй вектор, и построить вектор, соединяющий начало первого с концом второго – это будет:
а) разность первого и второго векторов
б) сумма первого и второго векторов +
в) нулевой вектор

10. Чем характеризуются скалярные величины?
а) численным значением и направлением
б) только численным значением +
в) только направлением

11. В чего изображается на графике нулевой вектор?
б) В виде точки +
а) В виде прямой
в) В виде направленного отрезком

12. Какое правило используется для сложения двух любых векторов?
а) Правило Пифагора
б) Правило треугольника
в) Правило параллелограмма +

13. Как называется вектор, начало которого совпадает с его концом
а) Нулевой +
б) Начальный
в) Точечный

14. Какой вектор направлен вниз к поверхности Земли?
а) вектор скорости свободно падающего тела +
б) вектор скорости автомобиля, движущего по горизонтальной дороге
в) вектор скорости взлетающей вверх ракеты

15. Как называется закон: сумма двух векторов не изменится от порядка слагаемых?
a) Переместительный законом +
б) сочетательный законом
в) правило параллелограмма

16. Автомобиль двигался по прямой дороге со скоростью 60 км/час. После знака ограничения скорости, автомобилист снизил скорость до 40 км час. Как изменился вектор скорости автомобиля.
а) Модуль вектора скорости увеличился в 1,5 раза, направление не изменилось
б) Модуль вектора скорости уменьшился в 1,5 раза, направление не изменилось
в) Модуль вектора скорости уменьшился в 1,5 раза, направление изменилось

17. Выберите скалярную физическую величину:
а) перемещение тела
б) скорость тела
в) масса тела +

18. При умножении векторной величины на скалярную получается:
а) скалярная величина
б) векторная величина +
в) в одних случаях скалярная, а в других векторная величина

19. Что такое модуль вектора?
а) направление вектора
б) числовое значение вектора +
в) координата вектора

20. Ракета вылетает под углом 30 градусов к горизонту со скоростью 300 м/с. Чему равен модуль вертикальной составляющей вектора скорости ракеты?
а) 150 м/с +
б) 260 м/с
в) 300 м/с

21. Как обозначают векторы?
а) буквами со стрелкой над ними +
б) буквами без стрелки над ними
в) цифрами

22. Угол между вектором силы и осью х составляет z. Модуль вектора силы равен F. Чему равен модуль составляющей вектора силы вдоль оси x?
а) F*sin(z)
б) F*cos(z) +
в) F*tg(z)

23. Как обозначают модуль вектора?
а) буквами со стрелкой над ними
б) буквами без стрелки над ними +
в) цифрами

24. Как называются два вектора с равными модулями, лежащие на параллельных прямых, если их направления противоположны?
а) противоположными +
б) коллинеарными
в) сонаправленными

25. Равными считаются векторы, у которых одинаковы:
а) модули
б) и модули, и направления +
в) направления

26.Какой вектор получится в результате умножения любого вектора на ноль?
а) единичный вектор
б) начальный вектор
в) нулевой вектор

27. Два вектора направлены перпендикулярно друг к другу. Их модули равны 3 и 4 соответственно. Чему равен модуль суммы этих векторов?
а) 5 +
б) 6
в) 7

28. Если при равномерном прямолинейном движении тела вектор перемещения разделить на время перемещения, что получится?
а) модуль скорости
б) вектор скорости +
в) модуль перемещения

29. Два вектора сонаправлены. Их модули равны 3 и 4 соответственно. Чему равен модуль суммы этих векторов?
а) 5
б) 6
в) 7 +

30. Если два вектора коллинеарны и их направления совпадают, то они называются:
а) сонаправленные +
б) коллинеарные
в) нулевые

31. Если из произвольной точки отложить первый вектор, а также второй вектор, и построить вектор, соединяющий конец второго вектора с концом первого – это будет:
а) разность первого и второго векторов +
б) сумма первого и второго векторов
в) нулевой вектор

📽️ Видео

СЛОЖЕНИЕ ВЕКТОРОВ закон правило треугольника 9 класс АтанасянСкачать

Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Геометрия 9 класс (Урок№7 - Разложение вектора по двум неколлинеарным векторам. Координаты вектора.)Скачать

Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать