Прочитав данную статью, вы узнаете, как найти высоту конуса. Приведенный в ней материал поможет глубже разобраться в вопросе, а формулы окажутся весьма полезными в решении задач. В тексте разобраны все необходимые базовые понятия и свойства, которые обязательно пригодятся на практике.
Видео:Длина окружности. Математика 6 класс.Скачать

Фундаментальная теория
Перед тем, как найти высоту конуса, необходимо разобраться с теорией.
Конус — фигура, которая плавно сужается от плоского основания (часто, хотя и необязательно, кругового) до точки, называемой вершиной.
Конус формируется набором отрезков, лучей или прямых, соединяющих общую точку с основанием. Последнее может ограничиваться не только окружностью, но и эллипсом, параболой или гиперболой.
Ось — это прямая (если таковая имеется), вокруг которой фигура имеет круговую симметрию. Если угол между осью и основой составляет девяносто градусов, то конус принято называть прямым. Именно такая вариация чаще всего встречается в задачах.
Если в основе лежит многоугольник, то объект является пирамидой.
Отрезок, соединяющий вершину и линию, ограничивающую основание, называют образующей.
Видео:№553. Найдите высоту конуса, если площадь его осевого сечения равна 6 дм2, а площадьСкачать
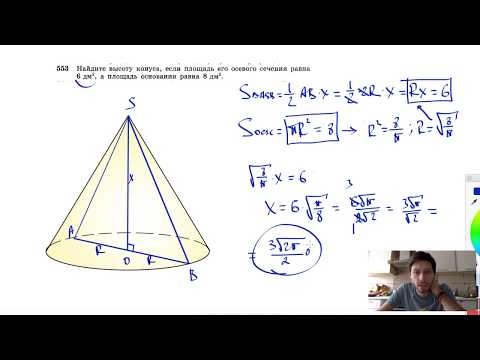
Как найти высоту конуса
Подойдем к вопросу с другой стороны. Для начала используем объем конуса. Чтобы его найти нужно вычислить произведение высоты с третьей частью площади.
Очевидно, что из этого можно получить формулу высоты конуса. Достаточно лишь сделать правильные алгебраические преобразования. Разделим обе части равенства на S и умножим на тройку. Получим:
Теперь вы знаете, как найти высоту конуса. Однако для решения задач вам могут понадобиться и другие знания.
Видео:+Как найти длину окружностиСкачать

Важные формулы и свойства
Приведенный ниже материал однозначно поможет вам в решении конкретных задач.
Центр массы тела находится на четвертой части оси, начиная от основы.
В проективной геометрии цилиндр — это просто конус, вершина которого находится на бесконечности.
Следующие свойства работают только для прямого кругового конуса.
- Даны радиус основания r и высота h, тогда формула для площади будет выглядеть так: П × r 2 . Соответственно изменится и окончательное уравнение. V = 1/3 × П × r 2 × h.
- Вычислить площадь боковой поверхности можно перемножив число «пи», радиус и длину образующей. S = П × r × l.
- Пересечение произвольной плоскости с фигурой является одним из конических сечений.
Часто встречаются задачи, где необходимо использовать формулу для объема усеченного конуса. Она выводится из обычной и имеет такой вид:
V = 1/3 × П × h × (R 2 + Rr + r 2 ), где: r -радиус нижнего основания, R — верхнего.
Всего этого будет вполне достаточно для решения разнообразнейших примеров. Разве что могут понадобиться знания, не связанные с этой темой, например, свойства углов, теорема Пифагора и другое.
Видео:№555. Высота конуса равна 10 см. Найдите площадь сечения, проходящего через вершину конусаСкачать

Радиус и высота конуса
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Свойства
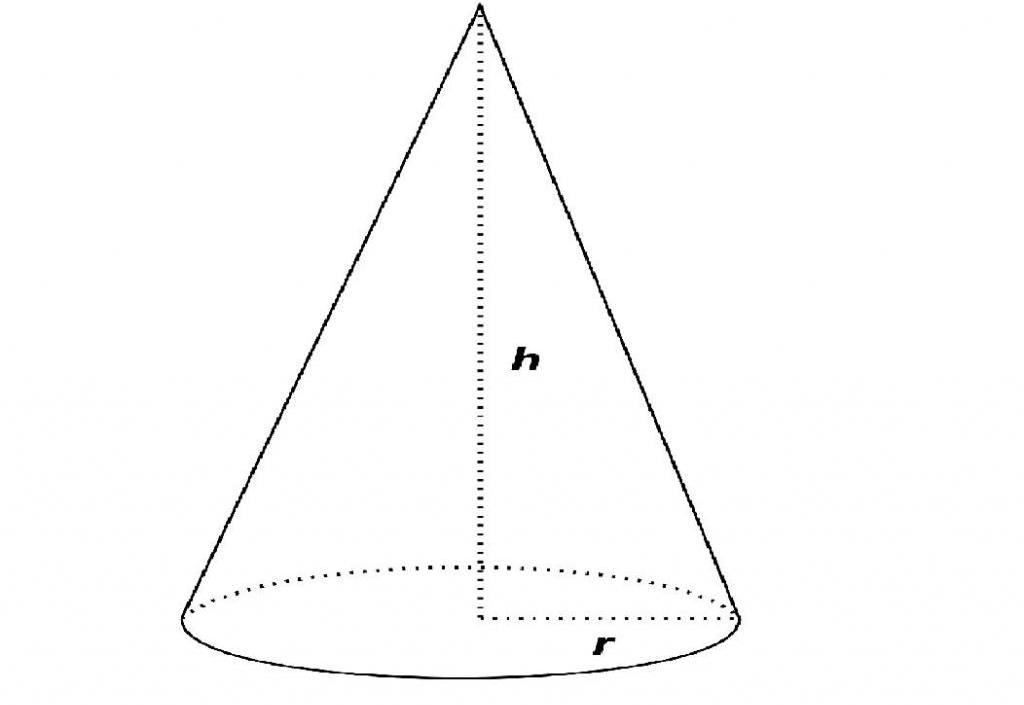
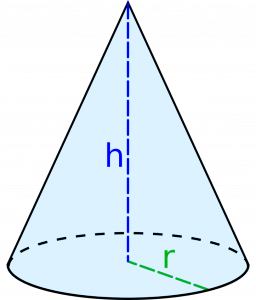
Через радиус конуса можно найти все параметры конуса, связанные с основанием, а значение высоты позволяет вычислить площади, объемы и все остальные объемные параметры конуса. Так, диаметр конуса равен удвоенному радиусу, периметр окружности в основании вычисляется по стандартной формуле через радиус, равно как и площадь основания. d=2r P=2πr S_(осн.)=πr^2
Прямоугольный треугольник, образованный высотой конуса, радиусом основания и образующей конуса, связывает эти три значения теоремой Пифагора, по которой можно вычислить неизвестную образующую, а также угол между образующей и основанием. Тем временем, угол α рассчитывается из равнобедренного треугольника, сформированного двумя образующими и диаметром из того принципа, что сумма всех углов в треугольнике равна 180 градусам. (рис.40.1, 40.2) l=√(h^2+r^2 ) tanβ=h/r α=180°-2β
Чтобы найти площадь боковой поверхности конуса, необходимо умножить радиус и апофему на число π. Площадь полной поверхности конуса состоит из площади его основания и площади боковой поверхности. В обеих формулах вместо апофемы нужно подставить квадратный корень через высоту и радиус, полученный по теореме Пифагора. S_(б.п.)=πrl=πr√(h^2+r^2 ) S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=πr(l+r)=πr(√(h^2+r^2 )+r)
Чтобы найти объем конуса, достаточно знать значения радиуса и высоты, тогда формула объема выглядит как произведение числа π на квадрат радиуса и высоту, деленное на три. V=1/3 S_(осн.) h=(πr^2 h)/3
Радиус сферы, вписанной в конус, зависит не только от радиуса основания конуса и его высоты, но и от образующей, поэтому чтобы вычислить радиус вписанной сферы конуса через радиус конуса и высоту, нужно вместо образующей подставить полученное для нее выше выражение. Радиус описанной сферы может быть представлен сразу формулой только с переменными радиуса и высоты. (рис.40.3, 40.4) r_1=hr/(l+r)=rh/(√(h^2+r^2 )+r) R=(h^2+r^2)/2h
Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Как найти высоту конуса если известен объем
Прочитав данную статью, вы узнаете, как найти высоту конуса. Приведенный в ней материал поможет глубже разобраться в вопросе, а формулы окажутся весьма полезными в решении задач. В тексте разобраны все необходимые базовые понятия и свойства, которые обязательно пригодятся на практике.
Видео:КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

Фундаментальная теория
Перед тем, как найти высоту конуса, необходимо разобраться с теорией.
Конус – фигура, которая плавно сужается от плоского основания (часто, хотя и необязательно, кругового) до точки, называемой вершиной.
Конус формируется набором отрезков, лучей или прямых, соединяющих общую точку с основанием. Последнее может ограничиваться не только окружностью, но и эллипсом, параболой или гиперболой.
Ось – это прямая (если таковая имеется), вокруг которой фигура имеет круговую симметрию. Если угол между осью и основой составляет девяносто градусов, то конус принято называть прямым. Именно такая вариация чаще всего встречается в задачах.
Если в основе лежит многоугольник, то объект является пирамидой.
Отрезок, соединяющий вершину и линию, ограничивающую основание, называют образующей.
Видео:№547. Высота конуса равна 15 см, а радиус основания равен 8 см. Найдите образующую конуса.Скачать

Как найти высоту конуса
Подойдем к вопросу с другой стороны. Для начала используем объем конуса. Чтобы его найти нужно вычислить произведение высоты с третьей частью площади.
Очевидно, что из этого можно получить формулу высоты конуса. Достаточно лишь сделать правильные алгебраические преобразования. Разделим обе части равенства на S и умножим на тройку. Получим:
Теперь вы знаете, как найти высоту конуса. Однако для решения задач вам могут понадобиться и другие знания.
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Важные формулы и свойства
Приведенный ниже материал однозначно поможет вам в решении конкретных задач.
Центр массы тела находится на четвертой части оси, начиная от основы.
В проективной геометрии цилиндр – это просто конус, вершина которого находится на бесконечности.
Следующие свойства работают только для прямого кругового конуса.
- Даны радиус основания r и высота h, тогда формула для площади будет выглядеть так: П × r 2 . Соответственно изменится и окончательное уравнение. V = 1/3 × П × r 2 × h.
- Вычислить площадь боковой поверхности можно перемножив число «пи», радиус и длину образующей. S = П × r × l.
- Пересечение произвольной плоскости с фигурой является одним из конических сечений.
Часто встречаются задачи, где необходимо использовать формулу для объема усеченного конуса. Она выводится из обычной и имеет такой вид:
V = 1/3 × П × h × (R 2 + Rr + r 2 ), где: r -радиус нижнего основания, R – верхнего.
Всего этого будет вполне достаточно для решения разнообразнейших примеров. Разве что могут понадобиться знания, не связанные с этой темой, например, свойства углов, теорема Пифагора и другое.
Конус — тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной
точки (вершины конуса) и проходящих через плоскую поверхность.
Иногда конусом называют часть такого тела, имеющую ограниченный объём и полученную объединением
всех отрезков, соединяющих вершину и точки плоской поверхности (последнюю в таком случае
называют основанием конуса, а конус называют опирающимся на данное основание).
Воспользуйтесь онлайн калькулятором для расчета объема пирамиды: объем конуса, онлайн расчет.
Для расчета объемов других тел воспользуйтесь этим калькулятором: калькулятор объемов фигур.
- Отрезок, соединяющий вершину и границу основания, называется образующей конуса.
- Объединение образующих конуса называется образующей (или боковой) поверхностью конуса.
Образующая поверхность конуса является конической поверхностью.
- Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого
отрезка), называется высотой конуса.
- Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине
конуса, внутри конуса).
- Если основание конуса имеет центр симметрии (например, является кругом или эллипсом) и
ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром, то
конус называется прямым. При этом прямая, соединяющая вершину и центр основания, называется
осью конуса.
- Косой (наклонный) конус — конус, у которого ортогональная проекция вершины на основание не
совпадает с его центром симметрии.
- Круговой конус — конус, основание которого является кругом.
- Прямой круговой конус (часто его называют просто конусом) можно получить вращением
прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось
- Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно
эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный
- Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся
между вершиной и основанием, называется усечённым конусом, или коническим слоем.
Объем конуса вычисляется по формуле:
где R — радиус основания конуса,