Множества треугольников разбили на подмножества (4 видео)

Понятие разбиения множества на классы

Дата добавления: 2014-09-06 ; просмотров: 8141 ; Нарушение авторских прав

Понятие множества и операций над множествами позволяют уточнить наше представление о классификации.

Любая классификация связана с разбиением некоторого множества объектов на подмножества.

3) объединение подмножеств совпадает с множеством А.

Если не выполнено хотя бы одно свойство, то классификацию считают неправильной.

Например, если множество треугольников разбить на остроугольные, прямоугольные и тупоугольные, то разбиение будет выполнено верно, т.к. выполнены все условия, данные в определении.

Если из множества треугольников выделить подмножества равносторонних, равнобедренных и разносторонних треугольников, то разбиения мы не получим, т.к. множество равносторонних треугольников является подмножеством равнобедренных треугольников, т.е. не выполняется второе условие разбиения множества на классы.

Пример 1. Пусть А – множество двузначных чисел. Рассмотрим на этом множестве свойство «быть четным».

А₂

А₁

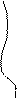
Множество А разбилось на два подмножества:

А₁ – множество четных чисел,

А₂ – множество нечетных чисел, при этом

Т.о. задание одного свойства приводит к разбиению этого множества на 2 класса.

Пример 2. Пусть А – множество треугольников. Рассмотрим на данном множестве два свойства: «быть прямоугольным» и «быть равнобедренным». При помощи этих свойств из множества треугольников можно выделить 2 подмножества: В – множество прямоугольных треугольников и С – множество равнобедренных треугольников. Эти множества пересекаются, но ни одно из них не является подмножеством другого.

По рисунку видно, что получилось 4 класса:

I – В Ç С – множество равнобедренных прямоугольных треугольников;

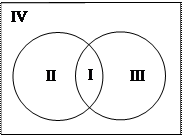
II – В Ç 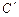– множество прямоугольных, но не равнобедренных треугольников;

III – 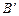Ç С – множество равнобедренных, но не прямоугольных треугольников;

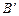
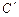
IV – Ç – множество не равнобедренных и не прямоугольных треугольников.

Т.о. с помощью двух свойств множество разбилось на 4 класса, таких, что их пересечение пусто, а их объединение составляет множество А.

Следует отметить, что задание двух свойств приводит к разбиению множества на 4 класса не всегда.

Пример 3. Пусть А – множество треугольников. Рассмотрим на данном множестве два свойства: «быть прямоугольным» и «быть остроугольным». При помощи этих свойств из множества треугольников можно выделить 2 подмножества: В – множество прямоугольных треугольников и С – множество остроугольных треугольников. Эти множества не пересекаются. По рисунку видно, что при помощи этих свойств множество треугольников разбивается на три класса:

I – множество прямоугольных треугольников;

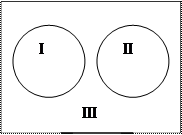
II – множество остроугольных треугольников;

III – множество не прямоугольных, не остроугольных треугольников.

Контрольные вопросы

1. При каких условиях считают, что множество разбито на классы?

2. Как определить число элементов в объединении двух или трех конечных множеств?

Содержание

Материалы тестовой работы по теме «Множества»
Просмотр содержимого документа «Материалы тестовой работы по теме «Множества»»
Понятие разбиения множества на классы с помощью одного, двух, трех свойств
🔥 Видео

Видео:ПОДМНОЖЕСТВА. Операции над множества. §14 алгебра 8 классСкачать

Материалы тестовой работы по теме «Множества»

тест для проведения среза по теме «Множества» для СПО «Дошкольное образование»

Просмотр содержимого документа
«Материалы тестовой работы по теме «Множества»»

Тест по теме «Множества»

Тест с выбором правильного ответа.

ИНСТРУКЦИЯ: Выберите букву с правильным ответом и занесите её в бланк ответов.

1. Определить какое из множеств является подмножеством А =

2. Какое из множеств определяет , если А = , B =

3. Какое из множеств определяет , если A = , B=

4. Множество треугольников разбили на подмножества разносторонних треугольников, равнобедренных треугольников и равносторонних треугольников. Произошло ли разбиение множества треугольников на классы?

5. На каком рисунке изображено объединение множеств А и В ()?

Тест по теме «Множества»

Тест с выбором правильного ответа.

ИНСТРУКЦИЯ: Выберите букву с правильным ответом и занесите её в бланк ответов.

1. Определить какое из множеств является подмножеством

2. Какое из множеств определяет , если А = , B =

3. Какое из множеств определяет , если A = , B =

4. Множество всех углов разбили на подмножества прямых, тупых и острых. Произошло ли разбиение множества углов на классы?

5. На каком рисунке изображено пересечение множеств А и В ()?

Видео:Подмножество, собственное подмножество и надмножество (видео 2) | Множества | АлгебраСкачать

Понятие разбиения множества на классы с помощью одного, двух, трех свойств

Понятия множества и операций над множествами позволяют уточнить наше представление о классификации – действии распределения объектов по классам.

Классификацию мы выполняем достаточно часто. Так, натуральные числа представляем как два класса – четные и нечетные. Углы на плоскости разбиваем на три класса: прямые, острые и тупые.

Любая классификация связана с разбиением некоторого множества объектов на подмножества. При этом считают, что множество Х разбито на классы Х₁, Х₂, …, Хn,…, если:

1) подмножества Х₁, Х₂, …, Хn,… попарно не пересекаются;

2) объединение подмножеств Х₁, Х₂, …, Хn, … совпадает с множеством Х.

Если не выполнено хотя бы одно из условий, классификацию считают неправильной. Например, если из множества Х треугольников выделить подмножества равнобедренных, равносторонних и разносторонних треугольников, то разбиения мы не получим, поскольку подмножества равнобедренных и равносторонних треугольников пересекаются (все равносторонние треугольники являются равнобедренными). В данном случае не выполнено первое условие разбиения множества на классы.

Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять при помощи свойств элементов множеств.

Рассмотрим, например, множество натуральных чисел. Его элементы обладают различными свойствами. Положим,. что нас интересуют числа, обладающие свойством «быть кратным 3». Это свойство позволяет выделить из множества натуральных чисел подмножество, состоящее из чисел, кратных 3. Тогда про остальные натуральные числа можно сказать, что они не кратны 3, т.е. получаем еще одно подмножество множества натуральных чисел. Так как выделенные подмножества не пересекаются, а их объединение совпадает с множеством натуральных чисел, то имеем разбиение этого множества на два класса.

Вообще, если на множестве Х задано одно свойство, то это множество разбивается на два класса. Первый – это класс объектов, обладающий этим свойством, а второй – дополнение первого класса до множества Х. Во втором классе содержатся такие объекты множества Х, которые заданным свойством не обладают. Такую классификацию называют дихотомической.

Рассмотрим ситуацию, когда для элементов множества заданы два свойства. Например, «быть кратным 3» и «быть кратным 5». При помощи этих свойств из множества натуральных чисел можно выделить два подмножества: А – подмножество чисел, кратных 3, и В – подмножество чисел, кратных 5. Эти множества пересекаются, но ни одно из них не является подмножеством другого. Проанализируем получившийся рисунок (справа). Конечно, разбиения множества натуральных чисел на подмножества А и В не произошло. Но круг, изображающий множество N, можно рассматривать как состоящий из четырех непересекающихся областей – на рисунке они пронумерованы. Каждая область изображает некоторое подмножество множества N. Подмножество I состоит из чисел, кратных 3 и 5; подмножество II – из чисел, кратных 3 и не кратных 5; подмножество III – из чисел, кратных 5 и не кратных 3; подмножество IY – из чисел, не кратных 3 и не кратных 5. Объединение этих четырех подмножеств есть множество N.

Таким образом, выделение двух свойств привело к разбиению множества N натуральных чисел на четыре класса.

Не следует думать, что задание двух свойств элементов множества всегда приводит к разбиению этого множества на четыре класса. Например, при помощи двух таких свойств «быть кратным 3» и «быть кратным 6» множество натуральных чисел разбивается на три класса: I – класс чисел, кратных 6; II – класс чисел, кратных 3; но не кратных 6; III — класс чисел, не кратных 3.