Как найти вектор ортогональный двум другим

Вектора a и b называются ортогональными, если угол между ними равен 90°. (рис. 1).

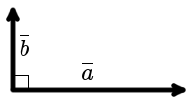рис. 1

Видео:2 42 Ортогональность векторовСкачать

Примеры задач на ортогональность векторов

Примеры плоских задач на ортогональность векторов

Так в случае плоской задачи для векторов a = < a_x ; a_y > и b = < b_x ; b_y > , условие ортогональности запишется следующим образом:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) = 2 — 2 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 3 · 7 + (-1) · 5 = 21 — 5 = 16

Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 = 2 n + 4
2 n + 4 = 0
2 n = -4
n = -2

Ответ: вектора a и b будут ортогональны при n = -2.

Примеры пространственных задач на ортогональность векторов

Так в случае пространственной задачи для векторов a = < a_x ; a_y ; a_z > и b = < b_x ; b_y ; b_z >, условие ортогональности запишется следующим образом:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 — 2 + 0 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 + 1 · (-8)= 2 n + 4 — 8 = 2 n — 4
2 n — 4 = 0
2 n = 4
n = 2

Ответ: вектора a и b будут ортогональны при n = 2.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Ортогональные векторы и условие ортогональности

В данной статье мы расскажем, что такое ортогональные векторы, какие существуют условия ортогональности, а также приведем подробные примеры для решения задач с ортогональными векторами.

Видео:Орт вектора. Нормировать вектор. Найти единичный векторСкачать

Ортогональные векторы: определение и условие

Ортогональные векторы — это векторы a ¯ и b ¯ , угол между которыми равен 90 0 .

Необходимое условие для ортогональности векторов — два вектора a ¯ и b ¯ являются ортогональными (перпендикулярными), если их скалярное произведение равно нулю.

Видео:Разложение вектора по базису. 9 класс.Скачать

Примеры решения задач на ортогональность векторов

Плоские задачи на ортогональность векторов

Если дана плоская задача, то ортогональность для векторов a ¯ = и b ¯ = записывают следующим образом:

a ¯ × b ¯ = a x × b x + a y × b y = 0

Задача 1. Докажем, что векторы a ¯ = и b ¯ = ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 1 × 2 + 2 × ( — 1 ) = 2 — 2 = 0

Ответ: поскольку произведение равняется нулю, то векторы являются ортогональными.

Задача 2. Докажем, что векторы a ¯ = и b ¯ = ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 3 × 7 + ( — 1 ) × 5 = 21 — 5 = 16

Ответ: поскольку скалярное произведение не равняется нулю, то и векторы не являются ортогональными.

Задача 3. Найдем значение числа n , при котором векторы a ¯ = и b ¯ = будут ортогональными.

Как решить?

Найдем скалярное произведение данных векторов:

a ¯ × b ¯ = 2 × n + 4 × 1 = 2 n + 4 2 n + 4 = 0 2 n = — 4 n = — 2

Ответ: векторы являются ортогональными при значении n = 2 .

Видео:Как разложить вектор по базису - bezbotvyСкачать

Примеры пространственных задач на ортогональность векторов

При решении пространственной задачи на ортогональность векторов a ¯ = и b ¯ = условие записывается следующим образом: a ¯ × b ¯ = a x × b x + a y × b y + a z × b z = 0 .

Задача 4. Докажем, что векторы a ¯ = и b ¯ = являются ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 1 × 2 + 2 × ( — 1 ) + 0 × 10 = 2 — 2 = 0

Ответ: поскольку произведение векторов равняется нулю, то они являются ортогональными.

Задача 5. Найдем значение числа n , при котором векторы a ¯ = и b ¯ = будут являться ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 2 × n + 4 × 1 + 1 × ( — 8 ) = 2 n + 4 — 8 = 2 n — 4 2 n — 4 = 0 2 n = 4 n = 2

Ответ: векторы a ¯ и b ¯ будут ортогональными при значении n = 2 .

Видео:Найдите разложение вектора по векторам (базису)Скачать

Как найти вектор, перпендикулярный вектору

Вы будете перенаправлены на Автор24

Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Понятие вектора и перпендикулярности векторов

Вначале надо разобраться, что является геометрическим вектором. Для этого сначала введем понятие отрезка.

Отрезком будем называть такую часть прямой, которая ограничена точками с двух сторон.

Концами отрезка будем называть точки, которые его ограничивают.

Для введения определения вектора один из концов отрезка назовем его началом.

Вектором (направленным отрезком) будем называть такой отрезок, у которого обозначено, какая граничная точка его начало, а какая является его концом.

Обозначение: $overline$ — вектор $AB$, имеющий начало в точке $A$, а конец в точке $B$.

Иначе одной маленькой буквой: $overline$ (рис. 1).

Нулевым вектором будем называть любую точку, которая принадлежит плоскости.

Введем теперь, непосредственно, определение коллинеарных векторов.

Два ненулевых вектора будем называть перпендикулярными (ортогональными), если они лежат на каких-либо перпендикулярных прямых (рис.2).

Готовые работы на аналогичную тему

Также введем определение скалярного произведения, которое будет нам необходимо далее.

Скалярным произведением двух данных векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.

Математически это может выглядеть следующим образом:

Скалярное произведение также можно найти с помощью координат векторов следующим образом

$overlineoverline=α_1 β_1+α_2 β_2+α_3 β_3$

Видео:Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать

Признак перпендикулярности через пропорциональность

Чтобы ненулевые векторы были перпендикулярны между собой, необходимо и достаточно, чтобы их скалярное произведение этих векторов равнялось нулю.

Необходимость: Пусть нам даны векторы $overline$ и $overline$, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они перпендикулярны друг другу. Тогда нам нужно доказать следующее равенство

Так как векторы $overline$ и $overline$ перпендикулярны, то угол между ними равняется $90^0$. Найдем скалярное произведение данных векторов по формуле из определения 6.

$overlinecdot overline=|overline||overline|cos⁡90^circ =|overline||overline|cdot 0=0$

Достаточность: Пусть верно равенство $overlinecdot overline=0$. Докажем, что векторы $overline$ и $overline$ будут перпендикулярны друг другу.

По определению 6, будет верно равенство

Следовательно, векторы $overline$ и $overline$ будут перпендикулярны друг другу.

Доказать, что векторы с координатами $(1,-5,2)$ и $(2,1,3/2)$ перпендикулярны.

Найдем скалярное произведение для этих векторов через формулу, данную выше

$overlinecdot overline=1cdot 2+(-5)cdot 1+2cdot frac=2cdot 5+3=0$

Значит, по теореме 1, эти вектор перпендикулярны.

Видео:Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Нахождение перпендикулярного вектора к двум данным векторам через векторное произведение

Введем вначале понятие векторного произведения.

Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют туже ориентацию, как и декартова система координат.

Чтобы найти векторное произведение, будем пользоваться формулой

Так как вектор векторного произведения двух векторов перпендикулярен обоим этим векторам, то он и будет иском вектором. То есть, для того, чтоб найти перпендикулярный для двух векторов вектор, нужно просто найти их векторное произведение.

Найти вектор, перпендикулярный к векторам с координатами $overline=(1,2,3)$ и $overline=(-1,0,3)$

Найдем векторное произведение данных векторов.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 19 07 2022

🔥 Видео

9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

89. Разложение вектора по двум неколлинеарным векторамСкачать

Единичный векторСкачать

Координаты вектора. 9 класс.Скачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

Нахождение координат вектора. Практическая часть. 9 класс.Скачать

A.7.4 Ортогонализация набора векторов. Процесс Грама-Шмидта.Скачать

18+ Математика без Ху!ни. Векторное произведение.Скачать

Координаты вектора в пространстве. 11 класс.Скачать