Как найти вектор обратной решетки (2 видео)

Обратная решетка и ее свойства

Обратная решетка. Понятия «обратная решетка» и «обратное пространство» занимают особое место в физике дифракции, в кристаллографин и вообще в физике конденсированного состояния. Эти понятия в физике были введены американским физиком и математиком Джо- зайей Уиллардом Гиббсом*. Рассмотрим вначале определение обратной решетки.

Выберем три базисных вектора а, Ь, с, определяющие элементарную ячейку решетки в обычном пространстве кристалла (в прямом пространстве). Тогда вектор трансляции будет иметь вид (1.2)

Здесь т, п, р — целые числа.

Введем новое пространство, в котором определим также три базисных вектора а*, Ь*, с* и вектор трансляции, размножающий решетку:

Здесь h, к, I пока просто целые числа.

Если введенные в (1.4) векторы удовлетворяют тождествам

то векторы а, Ь, с называются векторами прямой решетки, а векторы а*, Ь*, с* — векторами обратной решетки в обратном пространстве. Тогда целые числа h, k, I являются индексами Миллера плоскостей в прямой решетке.

Свойства обратной решетки. Векторы обратной решетки имеют два важных свойства (рис. 1.8).

1. Вектор обратной решетки Н_швсегда перпендикулярен плоскости прямой решетки с индексами (hkl).
2. Модуль вектора обратной решетки Н_ш всегда равен обратной величине межплоскостного расстояния для плоскостей в прямой решетке с индексами (hkl), т. е.

Первое свойство обратной решетки доказывается так. Если две любые прямые линии, лежащие в плоскости, перпендикулярны какому- либо вектору, не лежащему в этой плоскости, то этот вектор обязательно перпендикулярен выбранной плоскости.

Выберем три вектора АВ, СВ, СА, лежащих в плоскости АВС, и определим их величины:

Рис. 1.8. Два свойства обратной решетки:

а — вектор обратной решетки с индексами hkl перпендикулярен плоскостям прямой решетки с индексами Миллера (hkl); б — расстояния между плоскостями прямой решетки с индексами Миллера (.hkl) равны модулю вектора обратной

Из векторной алгебры известно, что два вектора перпендикулярны друг другу, если их скалярное произведение равно нулю. Воспользовавшись определением векторов обратной решетки, можно записать

Отсюда следует, что вектор Н перпендикулярен плоскости прямой решетки с индексами (hkl). Рассмотренные свойства векторов обратной решетки делают понятным построение стереографической проекции, когда плоскости заменяются нормалями к плоскостям, т. е. векторами обратной решетки.

Второе свойство обратной решетки также легко доказывается. Выберем в пространстве кристалла любую плоскость АВС с индексами Миллера (hkl) (см. рис. 1.9) Пусть вектор п — единичный вектор нормали к этой плоскости, а вектор R — текущий радиус-вектор точки, лежащей на плоскости АВС. Пусть также а — кратчайшее расстояние от начала координат до плоскости ЛВС.

Тогда уравнение такой плоскости можно записать в виде

Здесь n — единичный вектор нормали к плоскости;

о — кратчайшее расстояние от начала координат до плоскости;

где 5 — целое число (например, для плоскости, проходящей через начало координат, 5 = 0); d — межплоскостное расстояние для этой системы плоскостей.

Рис. 1.9. К выводу второго свойства вектора обратной решетки Н:

А, В, С — точки пересечения плоскости с осями координат; R — текущий радиус-вектор любой точки на плоскости; а — расстояние от начала координат

С учетом сделанных пояснений уравнение плоскости (1.6) представимо как

Запишем текущий радиус-вектор любой точки плоскости АВС:

Тогда уравнение плоскости (1.7) можно переписать в виде

В уравнении плоскости (1.8) выражение есть уравнение плоскости АВС. Следовательно,

что и требовалось доказать.

Для кубической сингонии величина межплоскостного расстояния определяется соотношением

где а — параметр решетки.

Для других сингоний формулы для межплоскостных расстояний приведены в прил. 9 (табл. П.9.10).

Обратное пространство является более общим понятием (в физике конденсированного состояния используются эквивалентные термины: «векторное пространство», «/с-пространство», «пространство дисперсии»). В обратном пространстве разыгрываются все дифракционные явления. Математическим аппаратом, описывающим связь прямого и обратного пространства, является преобразование Фурье (рис. 1.10) — гармонический ряд или интегралы Фурье (более подробно об этом см. в главе 3):

Puc. 1.10. Схематическое изображение связи прямого и обратного пространства

Понятие обратной решетки, введенное выше, — это частный случай обратного пространства. При первом знакомстве эта модель кажется очень абстрактной и сильно усложненным понятием. Однако это не просто удобный способ описания дифракционных явлений: именно в узлах обратной решетки располагаются дифракционные максимумы. Без такого понятия многие дифракционные явления довольно сложно описать. Понятия «обратная решетка», «обратное пространство» проходят красной нитью через всю физику твердого тела (зонная структура вещества, зоны Бриллюэна, Фурье-образ, ^-пространство, дисперсионные зависимости и др.).

Видео:2.1 Дифракция рентгеновских лучей и обратная решёткаСкачать

Обратная решетка

В физике твердого тела при анализе многих явлений (дифракция, движение электронов в потенциальном поле, рассеяние фотонов), связанных с периодическим расположением частиц, важную и полезную роль играет обратная решетка.

Обратная решетка представляет собой удобную абстракцию, позволяющую математически просто описать условия протекания того или иного явления в твердом кристаллическом теле.

Между векторами элементарных трансляций и периодами обратной решетки существует вполне определенная связь.

Пусть в кристаллической решетке элементарная ячейка определяется тремя элементарными трансляциями

с (рис. 1.14) [75]. Простейшими плоскими сетками являются сами координатные плоскости. Семейство плоскостей, параллельных векторам Ъ и

с (или, другими словами, плоскости семейства (100)), можно изобразить точкой на конце некоторого вектора а*, перпендикулярного к этим плоскостям. За длину этого вектора примем величину, обратную соответствующему межплоскостному расстоянию d _0Q = |Оа 11. Здесь Оп — проекция вектора а на нормаль к плоскости (100). Длину вектора а* можно определить из условия

Рис. 1.14. К выводу связи между параметрами прямой и обратной решеток

Кроме того, вектор а* откладывается вдоль нормали к плоскости так, чтобы для наблюдателя, смотрящего вдоль направления а*, вращение от b к

F совершалось по часовой стрелке. В векторном виде эти условия записываются тремя скалярными произведениями:

Два других вектора Ь* и с* определяют, исходя из сеток на других координатных плоскостях:

Проведем три вектора а*, Ь* и с* из какой-либо произвольной точки, кото рую назовем началом координат обратного пространства. Точечная решетка, построенная на этих векторах, является обратной решеткой для исходной (прямой) решетки кристалла.

Пусть объем элементарной ячейки прямой решетки У_яч, тогда

откуда в соответствии с соотношениями (1.1)—(1.3)

Углы между каждой парой векторов а*, 6*, с* обозначим о*, /3*, 7*. Они равны по величине двугранным углам триэдра, построенного на векторах 7Г, 6 , с, и могут быть вычислены из углов Q, /3, 7 между векторами прямой решетки по формулам:

Если в кристаллической решетке все углы прямые, то векторы элементарных трансляций а*, Ь*, с* обратной решетки параллельны векторам а , b ,

с прямой решетки и обратны им по величине. К этому результату можно прийти из формулы (1.5). Действительно, в этом случае объем элементарной ячейки У_яч = аЬс, а векторное произведение [6 с ] = be. Поэтому а* = 1/а.

Объем элементарной ячейки обратной решетки равен:

откуда

Таким образом, объем элементарной ячейки обратной решетки V* есть величина, обратная объему элементарной ячейки кристалла. Это соотношение является общим и применимо ко всем кристаллическим решеткам, в том числе и к непрямоугольным.

Любой вектор обратной решетки г* hkl = На* + Kb* + Lc* перпендикулярен плоскости (HKL) прямой кристаллической решетки, а длина его является величиной, обратной межплоскостному расстоянию:

Итак, прямая и обратная ячейки взаимно сопряжены. Если для описания кристаллической решетки вместо принятой вначале выбрать другую элементарную ячейку, то для элементарной ячейки обратной решетки получится также другая группа из трех векторов, но в целом решетка, построенная таким образом, будет идентична первой. Это следует из прямой связи между любым вектором одной решетки с одним только семейством плоскостей другой вне зависимости от координатных осей. Соответствие между двумя решетками, их взаимосвязь не зависят от выбора элементарной ячейки.

Решетка, обратная обратной решетке, является исходной (прямой) решеткой.

Каждый узел [[HKL]]* обратной решетки соответствуют семейству параллельных плоскостей (HKL) прямой решетки.

Обратная решетка сама является (по отношению к конкретной решетке Бравэ) решеткой Бравэ. Так, для примитивной кубической ячейки Бравэ со стороной а обратной является примитивная кубическая ячейка Бравэ со стороной 1 /а. Обратная к гранецентрированной есть объемноцентрированная решетка, а прямой объемноцентрированной соответствуют обратная гранецентрированная. Это утверждение будет доказано в одной из задач, приведенных в конце этой главы.

Видео:04 Вектора обратной решеткиСкачать

Как найти вектор обратной решетки

Зонные структуры Si и Ge, изображенные на рис. 31, вычерчены в обратном пространстве кристалла. Кое-что о k-пространстве было сказано, но этого явно недостаточно для отчетливого понимания закона дисперсии E(k). Существует несколько десятков пространственных конфигураций атомов: как выглядят их решетки, как найти обратные им, как применить теорию групп для их расчета, как учесть структурный фактор в гамильтониане? Ведь мы не касались вопросов составления ЛКАО-матрицы и не знаем, почему, собственно, ряд матричных элементов в ней равны нулю; есть параметры E_xx и E_xy, но почему-то отсутствуют E_zz, E_yy, E_xz и E_yz. Видимо, это как-то связано с симметрией электронных оболочек и устройством кристаллической решетки, но как?

Не все мы сможем рассказать, поскольку наша цель состоит не в том, чтобы всесторонне осветить задачи физики полупроводников, а в том, чтобы в выгодном свете представить теорию групп, обслуживающую эту самую физику полупроводников. Конечно, мы постараемся приложить максимум усилий для того, чтобы физическая сторона рассматриваемых явлений была понятна читателю, однако главная задача состоит в том, чтобы убедительно продемонстрировать эффективность конструктивной математики, к которой, в частности, принадлежит и теория групп. Будущие специалисты по материалам полупроводниковой техники для уяснения каких-то непонятных им вопросов материаловедения должны будут, очевидно, обратиться все же к литературе, ограниченный список которой приведен и в конце нашего учебника. Итак, обратное пространство кристалла, что это такое и как его найти.

Если узлы прямой решетки определить равенством

то узлы обратной решетки определятся равенством

причем базисные векторы обоих пространств ортогональны и нормированы. Последнее означает, что выполняется условие:

Из последних равенств немедленно вытекает связь между базисными векторами прямого и обратного пространства:

, , .

На рис. 32 показаны 14 пространственных решеток Браве; кубические — простая (P), объемоцентрированная (I) и гранецентрированная (F) для специалистов по материалам полупроводниковой техники являются особенно важными. Прямыми вычислениями можно убедиться, что обратная решетка для простой кубической (ПК) есть также ПК решетка; объемоцентрированной кубической решетке (ОЦК) отвечает гранецентрированная решетка (ГЦК), и наоборот; наконец, для гексагональной плотноупакованной решетки (ГПУ) обратной является опять же ГПУ.

К примеру, ГЦК — решетка определяется следующими тремя векторами:

Найдем по предыдущим формулам вектора обратной решетки, для чего сначала определим произведения векторов, стоящие в числителе и знаменателе дробей:

;

, ,

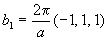
— три вектора определяют узлы ОЦК ячейки.

Процедуру вычисления векторов обратной решетки можно упростить, если прибегнуть к матрицам. Пусть координаты прямой ГЦК решетки a_i будут записаны элементами матрицы A, тогда обратная матрица A –1 = B укажет на координаты обратной ОЦК решетки b_i:

, .

К понятию обратной решетки можно прийти и другим путем. Если рассмотреть разложение какой-либо одномерной периодической функции f (r) = f (r + R), где R — пространственный период прямого пространства, в ряд Фурье:

то здесь появляется структурный фактор S(K), для которого K есть радиус-вектор, пробегающий узлы обратной решетки. Так как exp (iKR) = 1, структурный фактор найдется через интеграл:

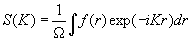
где Ω — объем элементарной ячейки прямой решетки, по которой и производится интегрирование. Поскольку обратная решетка определяется через коэффициенты преобразования Фурье, то k-пространство часто называют Фурье-пространством. Если в элементарной ячейке содержится N атомов с координатами ai, то распределение атомов в ней можно описать через δ-функцию:

В пределах элементарной ячейки R = 0, следовательно, суммирование производится только по атомам с координатами a_i, а структурный фактор сводится не к интегралу, а к простой сумме:

Для ГЦК с координатами

структурный фактор приобретает следующий конкретный вид:

Наиболее важные полупроводники, кремний и германий, имеют решетку алмаза, в которой присутствуют еще четыре атома с координатами:

Если начало координат выбрано не на атоме, а посередине между двумя атомами, то можно показать, что структурный фактор алмаза связан со структурным фактором ГЦК решетки по формуле:

Большая группа полупроводников, составленных из атомов III и V группы, II и VI группы Периодической таблицы Менделеева, например: GaAs, GaP, GaSb, InAs, InP и т.д., имеют решетку цинковой обманки (ZnS). Пространственная решетка ZnS, куда входят уже два рода атомов, теряет центр симметрии и структурный фактор становится антисимметричным:

На рис. 33 показаны элементарные ячейки: а) Cu, б) W, в) Mg, г) алмаза, д) NaCl, е) CsCl, ж) ZnS, з) ZnO, и) NiAs, к) CaF, л) CuAu, м) Cu3Au. Для каждой из них, в соответствии со структурным фактором, можно построить элементарные ячейки обратной решетки. Важно уметь строить одну-единственную элементарную ячейку, поскольку закон дисперсии E_n(k) приводится только для нее одной, и здесь на первый план выдвигается понятие зоны Бриллюэна (ЗБ). Первую ЗБ определяют как область в обратном пространстве, окружающую один из узлов обратной решетки и ограниченную набором плоскостей, проходящих через середины векторов, соединяющих в обратной решетке данную точку с ее ближайшими соседями.

На рис. 34 показана первая ЗБ для двумерной косоугольной решетки; на рис. 35 вычерчены уже десять ЗБ для двумерной квадратной решетки. Точно таким же половинным делением расстояния между двумя узлами определяется ЗБ в трехмерном пространстве. На рис. 36а приведены базисные векторы ОЦК решетки, а на рис. 36б — первая ЗБ, имеющая форму правильного ромбододекаэдра. На рис. 37 приведены первых четыре ЗБ для ГЦК решетки. На рис. 38 указаны симметричные точки (Г, L, Λ, Δ, …) первой ЗБ для ГЦК решетки, представляющая собой полуправильный многогранник Архимеда — усеченный октаэдр. Симметричные точки можно видеть на энергетических зонах, рассчитанных ЛКАО-методом (рис. 31а).

На рис. 39 вычерчены ЗБ для всех 14 решеток Браве, показанные в прямом пространстве на рис. 32. Соответствия между ЗБ и решетками Браве следующие: а) триклинная, б) моноклинная Р, в) моноклинная С, г) ромбическая Р, д) ромбическая С, е) ромбическая I, ж) ромбическая F, з) тетрагональная Р’, и) тетрагональная I, к) тригональная R, л) гексагональная Р, м) кубическая Р, н) кубическая F, о) кубическая I. Поскольку выбор ячеек может быть осуществлен несколькими способами, то существует и несколько вариантов ЗБ; поэтому для 14 решеток Браве вычерчено 22 ЗБ.