Как найти вектор графически

Векторы могут быть графически представлены направленными отрезками. Длина выбирается по определенной шкале, чтобы обозначить величину вектора, а направление отрезка представляетнаправление вектора. Например, если мы примем, что 1 см представляет 5 км/час, тогда северо-восточный ветер со скоростью 15 км/час будет представлен направленным отрезком длиной 3 cм, как показано на рисунке.

Вектор на плоскости это направленный отрезок. Два вектора равны если они имеют одинаковуювеличину и направление.

Рассмотрим вектор, нарисованный из точки A к точке B. Точка называется начальной точкой вектора, а точка B называется конечной точкой. Символическим обозначением для этого вектора есть (читается как “вектора AB”). Векторы также обозначается жирными буквами, такими как U, V и W. Четыре вектора на рисунке слева имеют одинаковую длину и направление. Поэтому они представляют равные веторы; то есть,

В контексте векторов мы применяем = чтобы обозначить их равность.

Длина, или величина выражается как ||. Для того, чтобы определить, равны ли векторы, мы находим их величины и направления.

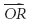
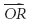
Пример 1 Векторы u, , w показаны на рисунке внизу. Докажите, что u = = w.

Решение Сначала мы находим длину каждого вектора с использованием формулы расстояния:
|u| = √ [2 — (-1)] 2 + (4 — 3) 2 = √ 9 + 1 = √ 10 ,
|| = √ [0 — (-3)] 2 + [0 — (-1)] 2 = √ 9 + 1 = √ 10 ,
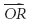
|w| = √ (4 — 1) 2 + [-1 — (-2)] 2 = √ 9 + 1 = √ 10 .
Отсюда
|u| = | 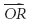= |w|.
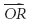
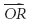
Векторы u, , и w, как видно из рисунка, вроде бы имеют одно и то же направление, но мы проверим их наклон. Если прямые, на которых они находятся, имеют одинаковые наклоны, то векторы имеют одно и то же направление. Рассчитываем наклоны:
Так как u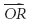, , и w имеют равные величины и одно и то же напраывление,
u = = w.

Имейте в виду, что равность векторов требует только одинаковой величины и одинакового направления, а не расположения в одном месте. На самом верхнем рисунке — пример равности векторов.

Предположим, что человек делает 4 шага на восток, а затем 3 шага на север. Тогда человек будет в 5 шагах от начальной точки в направлении, показанном слева. Вектор в 4 единицы длиной и с направление направо представляет 4 шага на восток и вектор 3 единицы длиной направление вверх представляет 3 шага на север. Сумма двух этих векторов есть вектор 5-ти шагов величины и в показанном направлении. Сумма также называется результирующим двух векторов.

В общем, два ненулевых вектора u и v могут быть сложены геометрически расположением начальной точки вектора v в конечную точку вектора u, и затем нахождением ветора, который имеет ту же самую начальную точку, что и вектор u и ту же самую конечную точку что и вектор v, как показано на рисунке внизу.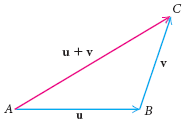

Суммой есть вектор, представленный направленным отрезком из точки A вектора u в конечную точку C вектора v. Таким образом, если u = и v = , тогда
u + v = + =

Мы также можем описать сложение векторов как совместное размещение начальных точек векторов, построением параллелограмма и нахождением диагонали параллелограмма. (на рисунке внизу.) Это сложение иногда называется как правило параллелограмма сложения векторов. Векторное сложение коммутативно. Как показано на рисунке, оба вектора u + v и v + u представлены одним и тем же направленным отрезком.

Если две силы F₁ и F₂ действуют на один объект, результирующая сила есть сумма F₁ + F₂ этих двух отдельных сил.

Пример Две силы в 15 ньютонов и 25 ньютонов действуют на один объект перпендикулярно друг другу. Найдите их сумму, или результирующую силу и угол, которая она образовывает с большей силой.

Решение Нарисуем условие задачи, в этом случае — прямоугольник, используя v или для представления результирующей. Чтобы найти ее величину, используем теорему Пифагора:
|v| 2 = 15 2 + 25 2 Здесь |v| обозначает длину или величину v.
|v| = √ 15 2 + 25 2
|v| ≈ 29,2.
Чтобы найти направление, отметим, что так как OAB есть прямым углом,
tanθ = 15/25 = 0,6.
Используя калькулятор, мы находим θ, угол, который большая сила образует с результирующей силой:
θ = tan — 1 (0,6) ≈ 31°
Результирующая имеет величину 29,2 и угол 31° с большей силой.

Пилоты могут корректировать направление их полёта, если есть боковой ветер. Ветер и скорость самолёта могут быть изображены как веторы.

Пример 3. Скорость самолёта и направление. Самолёт движется по азимуту 100° со скоростью 190 км/час, в то время как скорость ветра 48 км/ч, а его азимут — 220°. Найдите абсолютную скорость самолета и направление его движения с учетом ветра.

Решение Сначала сделаем рисунок. Ветер представлен и вектор скорости самолета есть . Результирующий вектор скорости есть v, сумма двух векторов. Угол θ между v и называется угол сноса.

Обратите внимание, что величина COA = 100° — 40° = 60°. Тогда величина CBA также равна 60° (противоположные углы параллклограмма равны). Так как сумма всех углов параллелограмма равна 360° и COB и OAB имеют одну и ту же величину, каждый должен быть 120°. По правилу косинусов в OAB, мы имеем
|v| 2 = 48 2 + 190 2 — 2.48.190.cos120°
|v| 2 = 47,524
|v| = 218
Тогда, |v| равно 218 км/ч. Согласно правилу синусов, в том же самом треуголнике,
48/sinθ = 218/sin120°,
или
sinθ = 48.sin120°/218 ≈ 0,1907
θ ≈ 11°
Тогда, θ = 11°, к ближайшему целому углу. Абсолютная скорость равна 218 км/ч, и направление его движения с учетом ветра: 100° — 11°, или 89°.

Если нам задан вектор w, мы можем найти два других вектора u и v, сумма которых есть w. Векторы u и v называются компонентами w и процесс их нахождения называется разложением, или представлением вектора его векторными компонентами.

Когда мы раскладываем вектор, обычно мы ищем перпендикулярные компоненты. Очень часто, однако, одна компонента будет параллельной оси x, и другая будет параллельна оси y. Поэтому, они часто называются горизонтальными и вертикальными компонентами вектора. На рисунке внизу вектор w = разложен как сумма u = и v = .

Горизонтальная компонента w есть u и вертикальная компонента — v.

Пример 4 Вектор w имеет величину 130 и наклон 40° относительно горизонтали. Разложите вектор на горизонтальные и вертикальные компоненты.

Решение Сначала мы нарисуем рисунок с горизонтальными и вертикальными векторами u и v, чья сумма есть w.

Из ABC, мы находим |u| и |v|, используя определения косинуса и синуса:
cos40° = |u|/130, или |u| = 130.cos40° ≈ 100,
sin40° = |v|/130, или |v| = 130.sin40° ≈ 84.
Тогда, горизонтальная компонента w есть 100 направо и вертикальная компонента w есть 84 вверх.

Видео:Графический метод решения задачи линейного программирования (ЗЛП)Скачать

Знакомимся с вектором

Основы линейной алгебры для тех, кого это миновало в универе.

Вы наверняка слышали много историй о программистах, которые учились в технических вузах, изучали высшую математику и теперь пользуются этими знаниями в программировании. И если кого-то это не коснулось, может быть ощущение, что он пропустил в жизни что-то важное.

Будем это исправлять. Попробуем разобрать некоторые базовые понятия из математики за пределами школьной программы. И заодно покажем, как оно связано с программированием и для каких задач полезно.

⚠️ Математики, помогайте. Мы тут многое упростили, поэтому будем рады увидеть ваши уточнения и замечания в комментариях.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Линейная алгебра

Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта. И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства.

Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.

Например, мы знаем, что если a + b = c , то a = c − b . Мы не знаем, что стоит на местах a, b или c, но для нас это такой абстрактный закон, который подтверждается практикой.

Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра.

В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения.

Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать.

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Что такое вектор

Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.

Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве

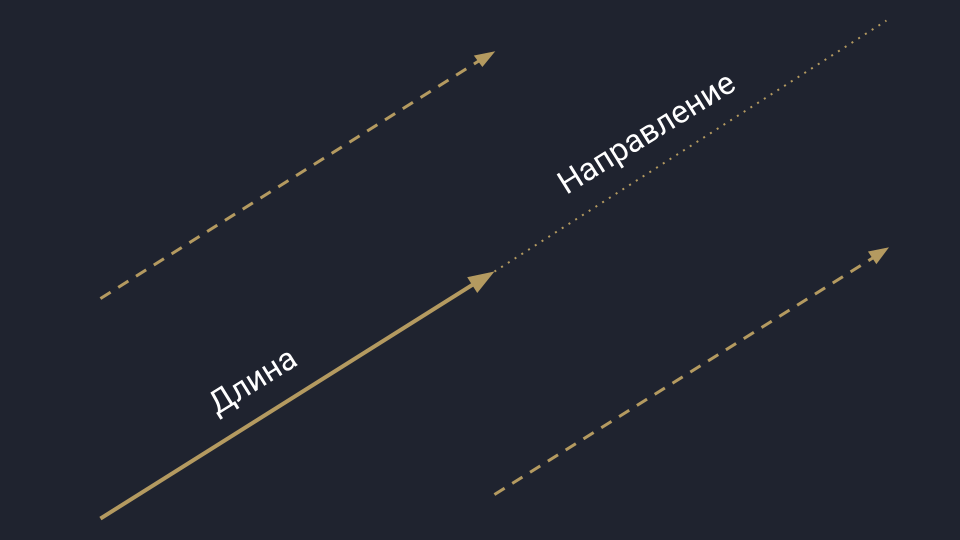
У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.

Аналитическое представление вектора: данные можно перевести в числа

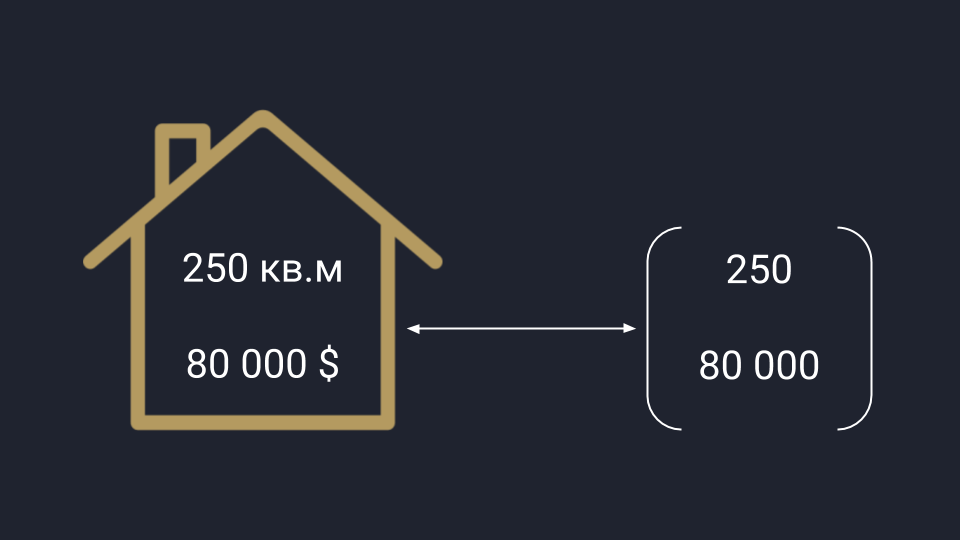
Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.

Математическое представление вектора: данные можно перевести в числа или график

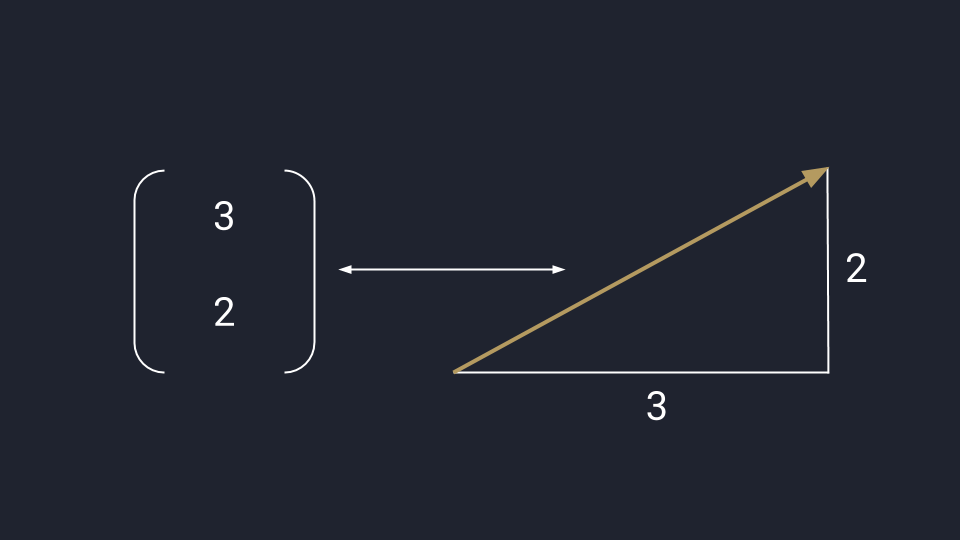
В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.

Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат

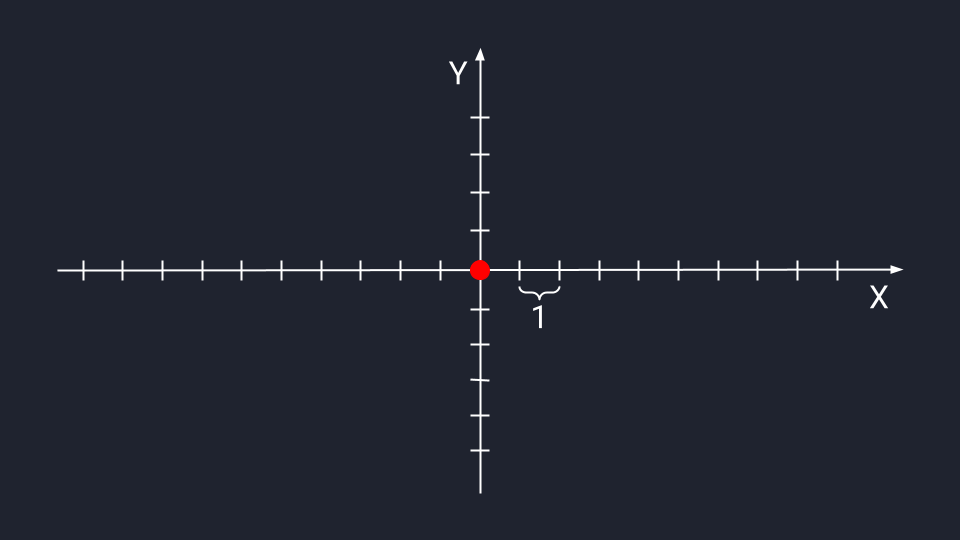
👉 Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.

Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.

Видео:Построение проекции вектора на осьСкачать

Как записывать

Вектор можно записать в строку или в столбец. Для строчной записи вектор обозначают одной буквой, ставят над ней черту, открывают круглые скобки и через запятую записывают координаты вектора. Для записи в столбец координаты вектора нужно взять в круглые или квадратные скобки — допустим любой вариант.

Строгий порядок записи делает так, что каждый набор чисел создаёт только один вектор, а каждый вектор ассоциируется только с одним набором чисел. Это значит, что если у нас есть координаты вектора, то мы их не сможем перепутать.

Способы записи вектора

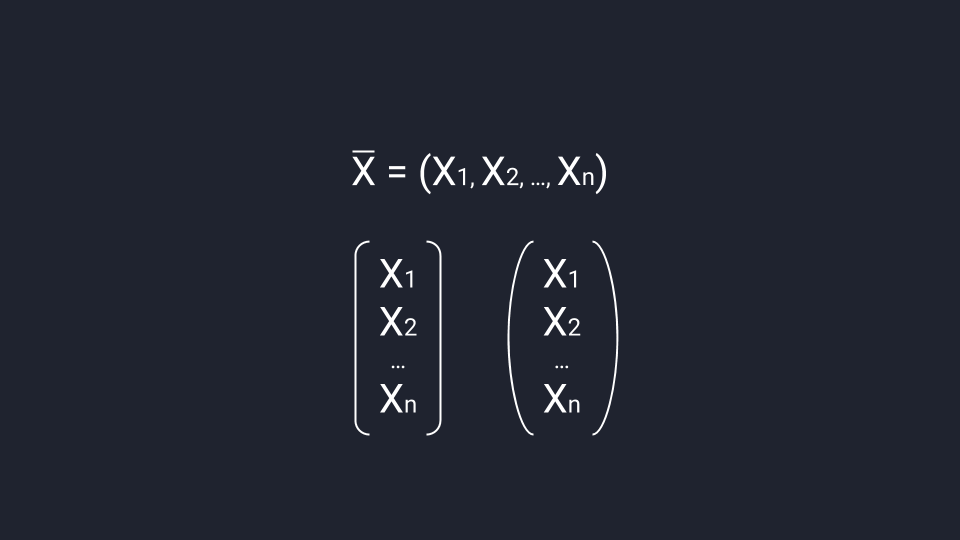
Скаляр

Помимо понятия вектора есть понятие скаляра. Скаляр — это просто одно число. Можно сказать, что скаляр — это вектор, который состоит из одной координаты.

Помните физику? Есть скалярные величины и есть векторные. Скалярные как бы описывают просто состояние, например, температуру. Векторные величины ещё и описывают направление.

Видео:18+ Математика без Ху!ни. Векторное произведение.Скачать

Как изображать

Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.

Графическое представление скаляра. Записывается в круглых скобках

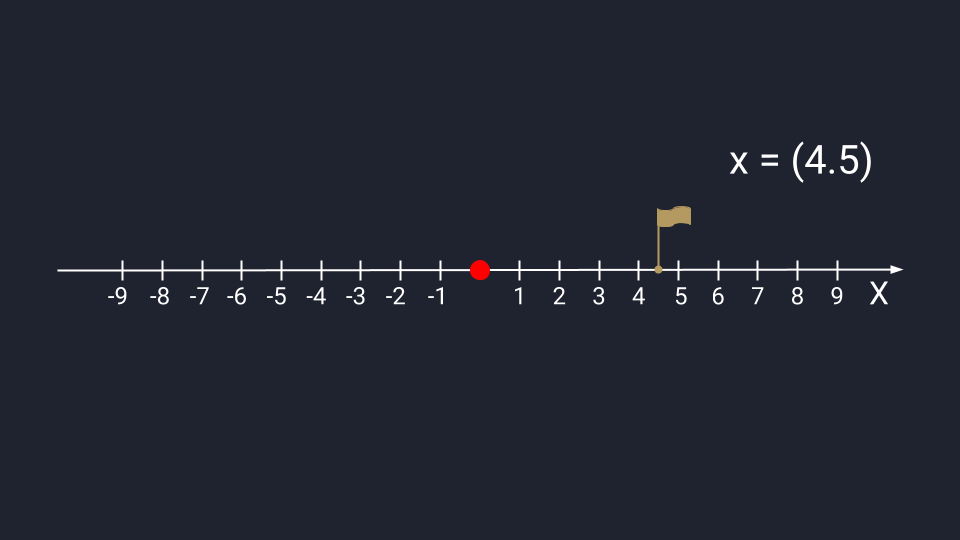
Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.

Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.

Графическое представление числового вектора в двух измерениях

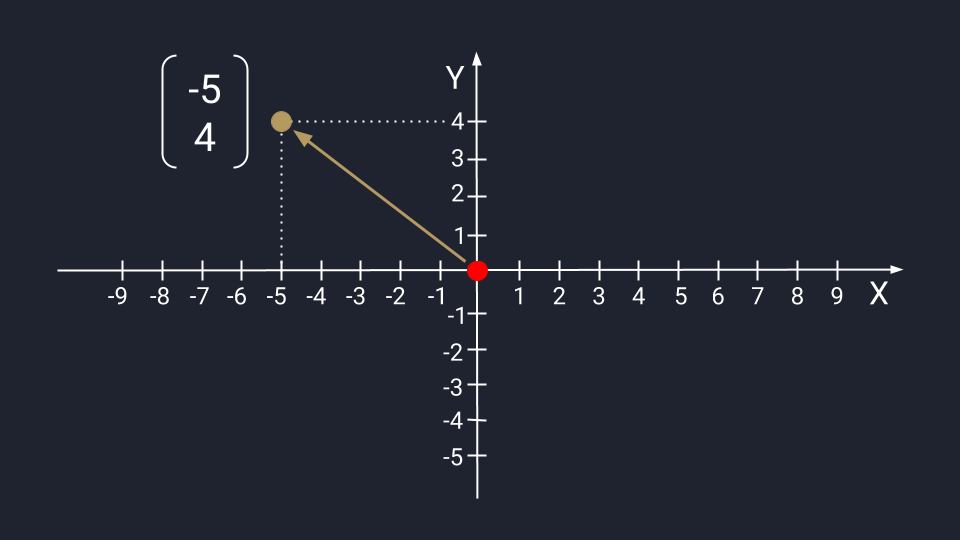
Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.

Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.

Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4

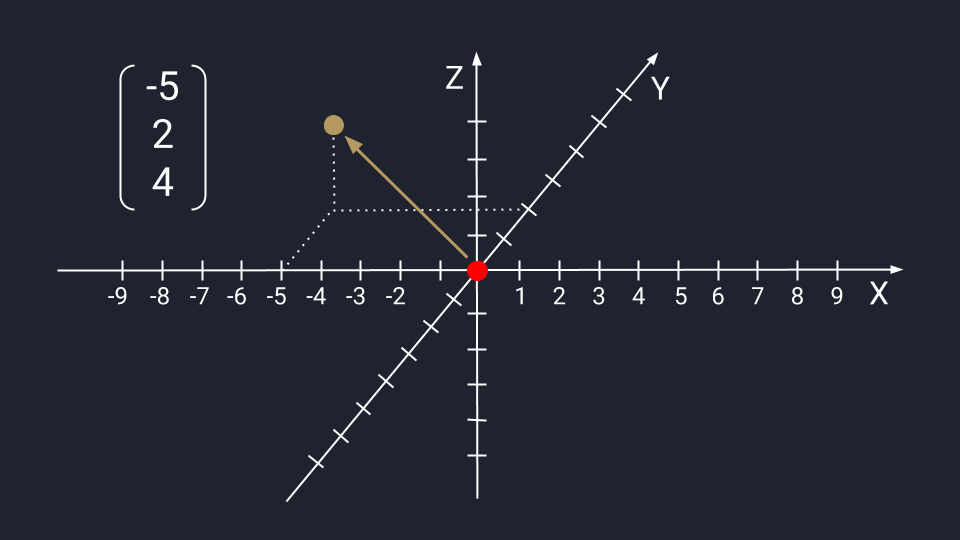
Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке. Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства.

Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.

Видео:Вычитание векторов. 9 класс.Скачать

И зачем нам это всё

Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:

• На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
• Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.

Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.

И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Что дальше

В следующий раз разберём операции с векторами. Пока мы готовим материал — рекомендуем почитать интервью с Анастасией Никулиной. Анастасия ведёт ютуб-канал по дата-сайнс и работает сеньором дата-сайентистом в Росбанке.

Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Сумма векторов: графический метод, примеры, решенные упражнения.

Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Содержание:

В векторная сумма это операция сложения между векторами, которая приводит к другому вектору. Векторы характеризуются величиной, а также направлением и смыслом. Следовательно, в общем случае невозможно сложить их, как это было бы со скалярными величинами, то есть путем сложения чисел.

Вектор, полученный из суммы нескольких векторов, называется результирующий вектор. В механике говорят о Равнодействующая сила, которая представляет собой векторную сумму всех сил, действующих на тело. Эта равнодействующая эквивалентна множеству или системе сил.

Чтобы полностью указать вектор суммы, необходимо указать величину и единицу, направление и смысл.

Важно отметить, что при сложении векторов они должны представлять одну и ту же физическую величину, поэтому векторная сумма является однородной операцией. Это означает, что мы можем добавлять одну силу к другой, но не силу со смещением, поскольку результат не имеет смысла.

Для нахождения результирующего вектора доступны несколько методов: графический и аналитический. Чтобы найти векторные суммы с помощью графических методов, мы начнем с простого представления вектора, а именно с ориентированного сегмента или стрелки, подобного этому:

Векторы обозначаются жирными буквами в печатном тексте или стрелкой над буквой, чтобы отличать их от соответствующих величин или скалярных величин. Например, величина вектора vЭто просто v.

Видео:Решение графических задач на силу АмпераСкачать

Графический метод сложения векторов

Чтобы добавить более двух копланарных векторов, полигональный метод или метод траверса, который состоит из трансляции себя параллельно каждому из векторов слагаемых. Характерной чертой векторов является то, что они инвариантны относительно сдвига, поэтому мы будем использовать это свойство для определения суммы.

Мы начинаем с любого из векторов, так как сложение векторов коммутативно и порядок слагаемых не влияет на сумму. Затем переводится второй вектор, сопоставляя его начало с концом первого.

Затем он переносится к следующему вектору и помещается следующим, следуя той же процедуре, которая заключается в совпадении начала координат с концом предыдущего. Продолжайте таким образом, пока не будет установлен последний вектор.

Результирующий вектор — это тот, который соединяет начало первого со свободным концом последнего. Название этого метода происходит от получившегося рисунка: многоугольник.

Видео:Нахождение координат вектора. Практическая часть. 9 класс.Скачать

пример

Возьмем для примера сумму двух векторов или Y v показано на рисунке выше.

Начиная с вектора или, переехал в вектор v чтобы его начало совпадало с концом первого. Результирующий вектор ш взят из происхождения или до конца v, образуя трехстороннюю фигуру: треугольник. Поэтому в этом частном случае процедура называется метод треугольника.

Обратите внимание на важную деталь: величина или модуль результирующего вектора не является суммой модулей добавленных векторов. Фактически, это почти всегда меньше, если векторы не параллельны.

Посмотрим, что происходит в этом случае ниже.

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Частный случай: сумма параллельных векторов

Описанный метод применим и к частному случаю, когда векторы параллельны. Рассмотрим следующий пример:

Оставлено вектору v в исходном положении и переводится в вектор или таким образом, что его происхождение совпадает с концом v. Теперь нарисован вектор, начиная с начала координат v и заканчивает конец или.

Это результирующий вектор ш а его размер — это сумма размеров слагаемых. Направление и смысл трех векторов одинаковы.

Результирующий вектор имеет максимальный модуль, если слагаемые образуют угол 0º друг с другом, как в примере. Если векторы расположены под углом 180º друг к другу, то результирующий вектор имеет минимальный модуль.

Видео:Орт вектора. Нормировать вектор. Найти единичный векторСкачать

Примеры сложения векторов

Видео:Единичный векторСкачать

— Смещения

Велосипедист проезжает сначала 3 км в северном направлении, а затем 4 км на запад. Ваше перемещение, которое мы называем р, легко найти с помощью метода треугольника плюс система отсчета, где отмечены стороны света:

Видео:Сложение векторов. Правило параллелограмма. 9 класс.Скачать

Шаги к векторному сложению

— Начальная точка совпадает с началом системы отсчета.

-По осям координат выбран масштаб, который в данном случае составляет 1 см = 1 км.

-Первое смещение нарисовано в масштабе d_1.

-Следующий d₁ второе смещение нарисовано d₂, также в масштабе.

-В результате смещения р — вектор, идущий от начала до конца d₂.

-Размерр измеряется градуированной линейкой, легко проверить, что R = 5.

-Наконец, угол, который р форма по горизонтали измерена с помощью транспортира и составляет θ = 37 0

Видео:Построить разность векторов.Скачать

— Результирующая скорость

Пловец хочет пересечь реку и для этого плывет со скоростью 6 км / ч перпендикулярно берегу, но его отклоняет течение со скоростью 4 км / ч.

Чтобы узнать его итоговую скорость, добавляются векторы скорости пловца, изображенного вертикально, и вектора скорости, отображаемого горизонтально.

Графическим методом получается результирующая скорость. v_р:

Отклонение, которое испытывает пловец, можно рассчитать следующим образом:

θ = arctg (4/6) = 33,7º вправо от начального направления

Величина его скорости увеличивается благодаря тому, что скорость реки складывается векторно. Его можно найти, аккуратно установив масштаб, как в примере выше.

Или с помощью тригонометрических соотношений 33,7º:

грех 33,7º = 4 / v_р

v_р = 4 / sin 33,7º = 7,21 км / ч

Видео:СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Упражнение решено

На частицу действуют следующие силы, величины которых указаны ниже:

Найдите равнодействующую силу.

Видео:Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Решение

Мы можем складывать графически, начиная с любого из векторов, поскольку векторная сумма коммутативна.

На рисунке A мы начали с F₁. Устанавливая масштаб, с помощью линейки и квадрата переносятся другие векторы, чтобы расположить их один за другим.

Вектор F_р направлено от происхождения F₁ до конца F₄. Его величина составляет 5,2 Н, и он образует угол 26,5 ° по отношению к горизонту.

На рисунке B была решена та же проблема, начиная с F₃ и заканчивая F₄, чтобы сравнятьсяF_р .

Многоугольники разные, но результат тот же. Читатель может провести тест, снова изменив порядок векторов.

Видео:Координаты вектора. 9 класс.Скачать

Ссылки

1. Бауэр, В. 2011. Физика для инженерии и науки. Том 1. Мак Гроу Хилл.
2. Бедфорд, 2000. А. Инженерная механика: Статика. Эддисон Уэсли.
3. Фигероа, Д. (2005). Серия: Физика для науки и техники. Том 1. Кинематика. Отредактировал Дуглас Фигероа (USB).
4. Джамбаттиста, А. 2010. Физика. 2-й. Эд. Макгроу Хилл.
5. Сирс, Земанский. 2016. Университетская физика с современной физикой. 14-го. Ред. Том 1.

Перекись водорода (H2O2): состав, свойства, применение, получение.

Анатидафобия: фобия шуток, связанная с утками, которые смотрят на нас

🎦 Видео

Как найти координаты вектора?Скачать