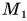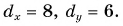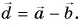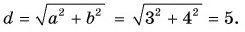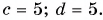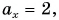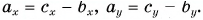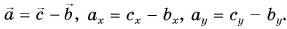По этой ссылке вы найдёте полный курс лекций по математике:
кинематике существуют три способа аналитического описания движения материальной точки в пространстве. Рассмотрим их, ограничившись случаем движения материальной точки на плоскости, что позволит нам при выборе системы отсчёта задавать лишь две координатные оси. Рис. 1 Рис. 2 1.
Векторный способ. В этом способе положение материальной точки А задаётся с помощью так называемого радиус-вектора г, который представляет совой вектор, проведённый из точки О, соответствующей началу отсчёта выбранной системы координат, в интересующую нас точку А (рис. 1). В процессе движения материальной точки её радиус-вектор может изменяться как по модулю, так и по направлению, являясь функцией времени г = r(t).
Геометрическое место концов радиус-вектора г (t) называют траекторией точки А. В известном смысле траектория движения представляет собой след (явный или воображаемый), который «оставляет за собой» точка А после прохождения той или иной области пространства. Понятно, что геометрическая форма траектории зависит от выбора системы отсчёта, относительно которой ведётся наблюдение за движением точки.
Пусть в процессе движения по некоторой траектории в выбранной системе отсчёта за промежуток времени At тело (точка А) переместилось из начального положения 1 с радиус-вектором Т в конечное положение 2 с радиус-вектором Т (рис. 2). Приращение А г радиус-вектора тела в таком случае равно: Вектор Аг, соединяющий начальное и конечное положения тела, называют перемещением тела. Отношение Аг/At называют средней скоростью (средним вектором скорости) vcp тела за время At: Способы описания движения.
Векторный способ. Координатный способ. Естественный (или траекторный) способ Вектор vcp колли неарен и сонаправлен с вектором Аг, так как отличается от последнего лишь скалярным неотрицательным множителем 1 / Аг. Предложенное определение средней скорости справедливо для любых значений At, кроме Д/ = 0. Однако ничто не мешает брать промежуток времени At сколь угодно малым, но отличным от нуля.
Для точного описания движения вводят понятие мгновенной скорости, то есть скорости в конкретный момент времени t или в конкретной точке траектории. С этой целью промежуток времени At устремляют к нулю. Вместе с ним будет стремиться к нулю и перемещение Аг. При этом отношение А/ / At стремится к определённому значению, не зависящему от At. Величина, к которой стремится отношение Аг / At при стремлении At к нулю, называется мгновенной скоростью v: Теперь заметим, что чем меньше At, тем ближе направление Аг к направлению касательной к траектории в данной точке.
Следовательно, вектор мгновенной скорости направлен по касательной к траектории в данной точке в сторону движения тела. В дальнейшем там, где это не повлечёт недоразумений, мы будем опускать прилагательное «мгновенная» и говорить просто о скорости v тела (материальной точки). Движение тела принято характеризовать также ускорением, по которому судят об изменении скорости в процессе движения.
Его определяют через отношение приращения вектора скорости Av тела к промежутку времени А/, в течение которого это приращение произошло.
Ускорением а тела называется величина, к которой стремится отношение Av / At при стремлении к нулю знаменателя At: При уменьшении At ориентация вектора Av будет приближаться к определённому направлению, которое принимается за направление вектора ускорения а . Заметим, что ускорение направлено в сторону малого приращения скорости, а не в сторону самой скорости! Способы описания движения. Векторный способ. Координатный способ.
Возможно вам будут полезны данные страницы:
Естественный (или траекторный) способ Таким образом, зная зависимость г(/), можно найти скорость v и ускорение а тела в каждый момент времени. В этой связи возникает и обратная задача о нахождении скорости v(t) и радиус-вектора r(t) по известной зависимости от времени ускорения а . Для однозначного решения этой задачи необходимо знать начальные условия, т. е. скорость v0 и радиус-вектор г0 тела в начальный момент времени / = 0.
Напомним, что в системе СИ единицами длины, скорости и ускорения являются соответственно метр (м), метр в секунду (м/с) и метр на секунду в квадрате (м/с2 2. Координатный способ. В этом способе положение материальной точки А на плоскости в произвольный момент времени t определяется двумя координатами хну, которые представляют собой проекции радиус-вектора г тела на оси Ох и Оу соответственно (рис. 3). При движении тела его координаты изменяются со временем, т. е. являются функциями V= y(t).
| Если эти функции известны |
то они определяют положение тела на плоскости в любой момент времени. В свою очередь, вектор скорости v можно спроецировать на оси координат и определить таким образом скорости i и v.. изменения координат тела (рис. 4). В самом деле, vx и vy будут равны значениям, к которым стремятся соответственно отношения Ах/А t и Ay/At при стремлении к нулю промежутка времени At. Аналогично с помощью проецирования вектора а определяются ускорения ах и ах тела по направлениям координатных осей.
Таким образом, зная зависимости л(/) и >>(/), можно найти не только положение тела, но и проекции его скорости и ускорения, а следовательно, модуль и направление векторов v и а в любой момент времени. Например, модуль вектора скорости будет равен v=yjvx2+vv2 , а его направление может быть задано углом между этим вектором и любой осью координат. Так, угол а между вектором v и осью Ох определяется отношением tga = vy!vx. Аналогичными формулами определяются модуль и направление вектора а .
Обратная задача — нахождение скорости и зависимостей x(t) и y(t) по заданному ускорению — будет иметь однозначное решение, если кроме ускорения заданы ещё и начальные условия: проекции скорости и координаты точки в начальный момент времени t = 0. 3. Естественный (или траекторный) сносов. Этот способ применяют тогда, когда траектория материальной точки известна заранее.
На заданной траектории LM (рис. 5) выбирают начало отсчёта — неподвижную точку О, а положение движущейся материальной точки А определяют при помощи так называемой дуговой координаты /, которая представляет собой расстояние вдоль траектории от выбранного начала отсчёта О до точки А. При этом положительное направление отсчёта координаты / выбирают произвольно, по соображениям удобства, например так, как рис ^ показано стрелкой на рисунке 5.
Движение тела определено, если известны его траектория, начало отсчёта О, положительное направление отсчёта дуговой координаты I и зависимость l(t). Следующие два важных механических понятия — это пройденный путь и средняя путевая скорость. По определению, путь AS — это длина участка траектории, пройденного телом за промежуток времени At. Ясно, что пройденный путь — величина скалярная и неотрицательная, а потому его нельзя сравнивать с перемещением А г, представляющем собой вектор.
Сравнивать можно только путь AS и модуль перемещения Аг . Очевидно, что AS > |Аг|. Средней путевой скоростью г>ср тела называют отношение пути AS к промежутку времени At, в течение которого этот путь был пройден: Определённая ранее средняя скорость vc? (см. формулу (1)) и средняя путевая скорость отличаются друг от друга так же, как Аг отличается от AS, но при этом важно понимать, что обе средние скорости имеют смысл только тогда, когда указан промежуток времени усреднения At.
Само слово «средняя» означает усреднение по времени. Пример 1. Городской троллейбус утром вышел на маршрут, а через 8 часов, проехав в общей сложности 72 км, возвратился в парк и занял своё обычное место на стоянке. Какова средняя скорость vcp и средняя путевая скорость г>ср троллейбуса? Способы описания движения.
Векторный способ. Координатный способ. Естественный (или траекторный) способ Решение. Поскольку начальное и конечное положения троллейбуса совпадают, то его перемещение А г равно нулю Аг = 0, следовательно, = 0 . Но средняя путевая скорость троллейбуса не vcp=Ar/At = 0 и рср равна нулю.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
- Проекция вектора на ось в физике — формулы и определения с примерами
- Как определяют проекцию вектора на ось
- Можно ли найти модуль и направление вектора по его проекциям на координатные оси
- Пример №1
- Пример №2
- Кинематика
- Механическое движение и его виды
- Относительность механического движения
- Правило сложения перемещений
- Правило сложения скоростей
- Относительная скорость
- Скорость
- Ускорение
- Равномерное движение
- График скорости (проекции скорости)
- График перемещения (проекции перемещения)
- Прямолинейное равноускоренное движение
- Свободное падение (ускорение свободного падения)
- Движение тела по вертикали
- Движение тела, брошенного горизонтально
- Движение тела, брошенного под углом к горизонту (баллистическое движение)
- Движение по окружности с постоянной по модулю скоростью
- 💡 Видео
Видео:Угол между векторами. 9 класс.Скачать

Проекция вектора на ось в физике — формулы и определения с примерами
Содержание:
Проекция вектора на ось:
Вы уже знаете, что вектор имеет модуль и направление. При решении задач часто используется понятие проекция вектора на ось. Что такое проекция вектора? Как ее определяют?
Начнем с понятия проекция точки на ось.
Проекция точки — это основание перпендикуляра, опущенного из данной точки на ось.
На рисунке 24 точка
Видео:Угол между векторами | МатематикаСкачать

Как определяют проекцию вектора на ось
Проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора, взятая со знаком «+» или «-». Знак «+» берут, если угол между вектором и осью острый, а знак «-» — если угол тупой.
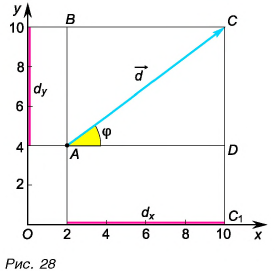
На рисунке 25 проекция вектора 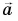
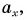
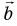
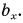
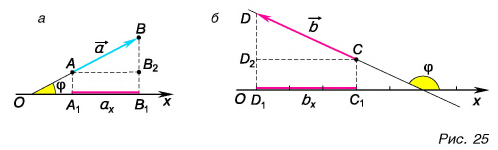
Проекция 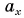
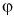
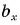
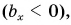
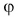
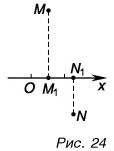
А если вектор перпендикулярен оси? Тогда его проекция на эту ось равна нулю (рис. 26).
Проекцию вектора можно выразить через его модуль и угол между вектором и осью.
Рассмотрим треугольник 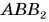
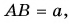
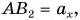
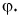
Проекция вектора на ось равна модулю вектора, умноженному на косинус угла между вектором и осью.
Это правило справедливо при любых углах между вектором и осью. Подтвердите это с помощью рисунков 25 и 26.
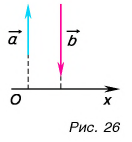
Обратим внимание на еще одно важное свойство проекций: проекция суммы векторов на ось равна сумме их проекций на эту ось.
С помощью рисунка 27, а, б убедитесь, что из векторного равенства 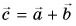
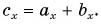
Можно ли найти модуль и направление вектора по его проекциям на координатные оси
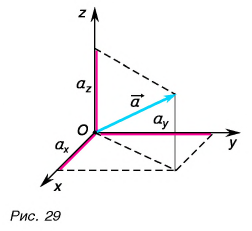
Рассмотрим вектор 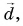
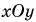
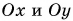
Модуль вектора 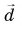
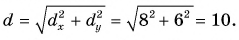
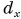
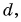
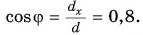
Таким образом, вектор, лежащий в заданной плоскости, полностью определяется двумя проекциями на оси координат.
Вектор в пространстве определяется тремя проекциями: 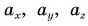
Главные выводы:
- Проекция вектора на ось — это длина отрезка, заключенного между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «-».
- Если угол между вектором и осью острый, то его проекция на эту ось положительна, если угол тупой — отрицательна, если прямой — равна нулю.
- Проекция вектора на ось равна произведению его модуля на косинус угла между вектором и осью.
- Проекция суммы векторов на ось равна сумме их проекций на эту ось.
Пример №1
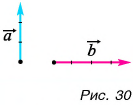
1. Определите сумму и разность взаимно перпендикулярных векторов 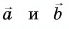
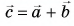
Решение
Сумму векторов 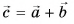
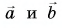
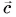
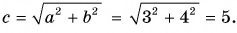
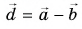
Модуль вектора 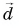
Ответ:
Пример №2
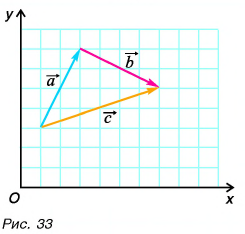
Выразите вектор 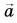
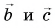
Решение
По правилу треугольника находим: 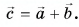
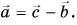
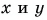
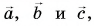
Вычислением убедимся, что проекции векторов связаны теми же равенствами, что и сами векторы:
Ответ:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Путь и перемещение
- Равномерное прямолинейное движение
- Прямолинейное неравномерное движение
- Прямолинейное равноускоренное движение
- Колебательное движение
- Физический и математический маятники
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Построение проекции вектора на осьСкачать

Кинематика
Механика — это раздел физики, изучающий механическое движение тел.
Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.
Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если
- расстояние, которое проходит тело, много больше его размера;
- расстояние от данного тела до другого тела много больше его размера;
- тело движется поступательно.
Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.
Важно!
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.
Основная задача механики — определить положение тела в пространстве в любой момент времени.
Видео:Урок 9. Проекции вектора на координатные осиСкачать

Механическое движение и его виды
Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение может быть:
1. по характеру движения
- поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
- вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
- колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;
2. по виду траектории
- прямолинейным — это движение, траектория которого прямая линия;
- криволинейным — это движение, траектория которого кривая линия;
- равномерным — движение, при котором скорость тела с течением времени не изменяется;
- неравномерным — это движение, при котором скорость тела с течением времени изменяется;
- равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
- равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.
Видео:Как находить угол между векторамиСкачать

Относительность механического движения
Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.
Правило сложения перемещений
Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:
где ( S ) — перемещение тела относительно неподвижной системы отсчета;
( S_1 ) — перемещение тела относительно подвижной системы отсчета;
( S_2 ) — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.
Правило сложения скоростей
Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:
где ( v ) — скорость тела относительно неподвижной системы отсчета;
( v_1 ) — скорость тела относительно подвижной системы отсчета;
( v_2 ) — скорость подвижной системы отсчета относительно неподвижной системы отсчета.
Относительная скорость
Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.
Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_ ) :
Определим скорость второго тела относительно первого ( v_ ) :
Следует помнить, что траектория движения тела и пройденный путь тоже относительны.
Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:
Если скорости направлены под углом ( alpha ) друг к другу, то относительная скорость рассчитывается по теореме косинусов:
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Скорость
Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.
Обозначение — ( v ) , единицы измерения — м/с (км/ч).
Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:
Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:
Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.
Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.
Видео:Нахождение угла между векторами через координаты. 9 класс.Скачать

Ускорение
Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.
Обозначение — ( a ) , единица измерения — м/с 2 .
В векторном виде:
где ( v ) – конечная скорость; ( v_0 ) – начальная скорость;
( t ) – промежуток времени, за который произошло изменение скорости.
В проекциях на ось ОХ:
где ( a_n ) – нормальное ускорение, ( a_ ) – тангенциальное ускорение.
Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:
Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:
Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.
Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_ ) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_ ) = 0, ( a_n ) = 0, ( v ) ≠ 0, то тело движется равномерно по прямой;
если ( a_ ) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_ ) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_ ) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.
Видео:Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

Равномерное движение
Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.
Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:
Проекция вектора скорости на ось ОХ:
Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:
График скорости (проекции скорости)
График скорости (проекции скорости) представляет собой зависимость скорости от времени:
График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ( t ) , тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ) , тело движется против оси ОХ.
Перемещение при равномерном движении – это величина, равная произведению скорости на время:
Проекция вектора перемещения на ось ОХ:
График перемещения (проекции перемещения)
График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:
График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ) , тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ) , тело движется против оси ОХ.
По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ) . Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Координата тела при равномерном движении рассчитывается по формуле:
График координаты представляет собой зависимость координаты от времени: ( x=x(t) ) .
График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:
График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:
Видео:Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Прямолинейное равноускоренное движение
Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:
При движении с ускорением скорость может как увеличиваться, так и уменьшаться.
Скорость тела при равноускоренном движении рассчитывается по формуле:
При разгоне (в проекциях на ось ОХ):
При торможении (в проекциях на ось ОХ):
График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:
График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ( a_x ) > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) ( v_ ) > 0, ( a_x ) > 0.
График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_ ) > 0, ( a_x ) ( v_ ) ( a_x ) ( t_2-t_1 ) . Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Перемещение при равноускоренном движении рассчитывается по формулам:
Перемещение в ( n ) -ую секунду при равноускоренном движении рассчитывается по формуле:
Координата тела при равноускоренном движении рассчитывается по формуле:
Видео:100 тренировочных задач #135 Угол между векторамиСкачать

Свободное падение (ускорение свободного падения)
Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.
Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).
Обозначение – ( g ) , единицы измерения – м/с 2 .
Важно! ( g ) = 9,8 м/с 2 , но при решении задач считается, что ( g ) = 10 м/с 2 .
Движение тела по вертикали
Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:
Если тело падает вниз без начальной скорости, то ( v_0 ) = 0.
Время падения рассчитывается по формуле:
Тело брошено вверх:
Если брошенное вверх тело достигло максимальной высоты, то ( v ) = 0.
Время подъема рассчитывается по формуле:
Движение тела, брошенного горизонтально
Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали со скоростью ( v_0=v_ ) ;
- равноускоренного движения по вертикали с ускорением свободного падения ( g ) и без начальной скорости ( v_=0 ) .
Скорость тела в любой момент времени:
Угол между вектором скорости и осью ОХ:
Движение тела, брошенного под углом к горизонту (баллистическое движение)
Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали;
- равноускоренного движения по вертикали с ускорением свободного падения.
Скорость тела в любой момент времени:
Угол между вектором скорости и осью ОХ:
Время подъема на максимальную высоту:
Максимальная высота подъема:
Максимальная дальность полета:
Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ( v_0 ) , с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ( alpha ) , под которым тело брошено, будет равен углу, под которым оно упадет.
При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:
Это облегчает решение задач:
Видео:Как разложить силы на проекции (динамика 10-11 класс) ЕГЭ по физикеСкачать

Движение по окружности с постоянной по модулю скоростью
Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.
Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.
Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ( a_ ) , единицы измерения – м/с 2 .
Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ( T ) , единицы измерения – с.
где ( N ) – количество оборотов, ( t ) – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ( nu ) , единицы измерения – с –1 (Гц).
Период и частота – взаимно обратные величины:
Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ( v ) , единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:
Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ( omega ) , единицы измерения – рад/с .
Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:
Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:
Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:
Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ( v_1 ) , и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ) , то относительно дороги мгновенная скорость разных точек колеса различна.
Мгновенная скорость нижней точки ( (m) ) равна нулю, мгновенная скорость в верхней точке ( (n) ) равна удвоенной скорости ( v_1 ) , мгновенная скорость точки ( (p) ) , лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ( (c) ) – по теореме косинусов.
💡 Видео
найти угол между единичными векторамиСкачать

ФИЗИКА 10 класс. Проекции вектора на оси координат | ВидеоурокСкачать

Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Проекции вектораСкачать

Векторные величины Проекция вектора на осьСкачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

11 класс, 5 урок, Угол между векторамиСкачать