Как найти центр окружности цилиндра равна

Видео:Найти центр кругаСкачать

Быстрый способ, как найти центр окружности

В данном обзоре автор поделится с нами довольно простым способом, как быстро найти центр окружности.

Для этого нам потребуется всего два предмета: угольник и карандаш. Первым делом необходимо провести прямую линию в любом месте окружности.

Советуем также прочитать: как изготовить своими руками антенну для усиления 4G сигнала на даче или в частном доме.

После того, как начертили линию, измеряем длину, и делим это расстояние ровно пополам.

В данном случае длина линии составляет 210 мм. Разделив ее пополам, получаем 105 мм — ставим в этом месте отметку.

С помощью угольника проводим вторую линию, которая должна быть перпендикулярна первой (то есть проходить под углом 90 градусов).

Видео:Не каждый знает как найти центр окружности без циркуля! #ShortsСкачать

Основные этапы работ

На следующем этапе проделываем те же операции с другой стороны окружности (только не параллельно, а немного в стороне).

Чертим линию, измеряем ее длину (в данном случае — 218 мм), делим пополам (109 мм) и откладываем в этом месте точку. После этого проводим перпендикулярную линию, как и в предыдущем случае.

Пересечение двух линий, которые мы чертили под углом 90 градусов, и будет являться центром круга.

Подробно об этом способе можно посмотреть на видео ниже. Статья подготовлена на основе видео с YouTube канала « ПОГРАНЕЦ 13 ».

Видео:Как найти центр круга в мастерской (4 способа)Скачать

Как найти Как найти центр окружности?

Видео:4K Как найти центр окружности, how to find the center of a circleСкачать

Как найти центр отверстия?

Через точки пересечения дуг проводят две прямые по направлению к центру до их пересечения в точке О. Точка пересечения этих прямых, и будет искомым центром отверстия.

Видео:Как найти центр круга с помощью подручных средств? ЛЕГКО.Скачать

Как найти центр окружности из уравнения?

Уравнение окружности ω (A; R) имеет вид (x – a) 2 + (y – b) 2 = R 2 , где a и b – координаты центра A окружности ω (A; R) .

Видео:Быстро и легко определяем центр любой окружностиСкачать

Чем размечают отверстия?

Размечать центровые отверстия в деталях диаметром до 40 мм лучше при помощи специального приспособления, называемого колоколом. Оно состоит из корпуса, конического раструба и кернера, перемещаемого в корпусе.

Видео:Как найти центр кругаСкачать

Как найти центр окружности на плоской заготовки?

Есть и совсем простой способ нахождения центра плоской заготовки круглой формы. Всего-то нужно обвести её по периметру, положив на лист бумаги, затем вырезать по начерченной линии круг, согнуть его вчетверо и центр будет найден. Он находится точно на линии пересечения сгибов.

Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Как правильно разметить отверстия?

Разметка отверстий для сверления.

1. Определить расположение отверстия по рабочему чертежу. Аккуратно отмерить расстояние отверстия от обоих краев доски. .
2. Наколите центр отверстия шилом. .
3. Если должны совпасть отверстия, просверленные в двух досках, зажмите обе доски в тисках.

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Исследовательская работа по математике: «Как определить центр окружности»

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №1 с. Александров – Гай

Исследовательская работа по математике:

Подготовил: Амиров Марат, ученик 6 «а»

класса МБОУ СОШ №1 с. Александров – Гай

Руководитель: , учитель математики МБОУ СОШ №1 с. Александров — Гай

С. Александров – Гай

Глава 1 «Способы нахождения окружности» …………………………………..4

Глава 2 «Практическая часть»…………………………………………………..6

Список литературы и источников………………………………………………12

Окружность — совокупность точек, находящихся на равном расстоянии от одной точки, называемой центром. Однако в тех случаях, когда вам дана одна только окружность, нахождение ее центра может быть непростой задачей. Поэтому цель моей исследовательской работы: изучить способы определения центра окружности. Исходя из цели были поставлены задачи:

— найти самый простой способ определения центра окружности;

— сравнить несколько способов определения центра окружности;

— практические способы определения центра окружности.

Актуальность ислледовательской работы заключается в том, что в повседневной жизни людей часто приходится находить центр окружности, но не каждый знает как это правильно сделать. Поэтому изучение данной темы поможет найти правильное решение проблемы и определить оптимальный вариант для человека любой професии.

При написании исследовательской работы были использованны электронные источники и литература. Электронные источники помогли найти теоретический материал по теме, а учебники по математике были использованны для подбора задач и практической части работы.

Глава 1. Способы нахождения центра окружности.

1.Самый простой способ нахождения центра окружности — согнуть лист бумаги, на котором она начерчена, следя на просвет, чтобы окружность оказалась сложена точно пополам. Полученная линия сгиба будет одним из диаметров заданной окружности. Затем лист можно согнуть в другом направлении, получив тем самым второй диаметр. Точка их пересечения и будет центром окружности.

2. Для того чтобы найти центр окружности, надо сначала вписать ее в квадрат. То есть все стороны четырехугольника должны касаться круга. Для этого проведите с помощью линейки четыре ровные линии. Теперь соедините по диагонали два противоположных угла. Следите за тем, чтобы линия разбивала угол квадрата на две равные части. Соедините прямыми все 4 угла квадрата. Точка пересечения данных прямых и будет центром окружности.

3. Для любого треугольника центр описанной окружности находится в точке пересечения срединных перпендикуляров. Если этот треугольник — прямоугольный, то центр описанной окружности всегда совпадает с серединой гипотенузы. Следовательно, если вписать в окружность прямоугольный треугольник, то его гипотенуза будет диаметром этой окружности.
В качестве трафарета для этого способа подойдет любой прямой угол — школьный или строительный угольник, или просто лист бумаги. Поместите вершину прямого угла в любую точку окружности и сделайте отметки там, где стороны угла пересекают границу круга. Это конечные точки диаметра.
Тем же способом найдите второй диаметр. В точке их пересечения

4.На круглую деталь накладываем лист бумаги так, что бы один его угол находился на окружности или крае круга. И отмечаем точки, где лист соприкасается другими краями с кругом. Отмечаем эти точки.

Проводим прямую линию между отмеченными точками. Расстояние между ними является диаметром этого круга. Обрезаем лишнюю бумагу и проводим на детали прямую линию — диаметр.

Достаточно переместить наш треугольник в другое положение и нарисовать еще один диаметр круга, как тут же в точке пересечения диаметров мы и получим искомый центр окружности…

5. Диаметр и радиус окружности.

Диаметр окружности — это отрезок прямой, соединяющий пару наиболее удаленных друг от друга точек окружности, проходящий через центр окружности. Слово «диаметр» произошло от греческого слова «diametros» — поперечный. Обычно диаметр обозначается латинской буквой D или значком Ø.

Диаметр можно найти по формуле: D = 2R, где диаметр равен удвоенному радиусу окружности.
Радиус — расстояние от центра до любой точки окружности. Обозначается латинской R.
Если известен радиус окружности, допустим, он равен 8 см, то значит D = 2 * 8 = 16 см.

Радиус окружности определяется по формуле : R=D:2

» width=»390″ height=»299 >
Глава 2 «Практическая часть»

1) Прямой угол детали закруглен дугой радиуса R

Для решения задачи с центром в вершине прямого угла проводят окружность радиуса R, которая пересекает стороны прямого угла в точках А и В.

С центрами в точках А и В строят еще две окружности радиуса R; С – их точка пересечения. Дуга окружности радиуса R с центром в точке С и будет искомым закруглением.

Произвольный угол детали закруглить дугой радиуса R

Решение: На расстоянии R от сторон угла проводят соответствующие параллельные им прямые. О — их пересечение. Затем строим окружность с центром О, радиуса R

Даны две параллельные прямые и точка А между ними. Как построить окружность, касающуюся данных прямых и проходящих через данную точку?

1) Построим любую окружность, касающуюся двух прямых (центр окружности находим, разделив ее пополам)

2) Проведем через А прямую, равную данным. Она пересечет построенную окружность в точках В и С. Перед ними центр построенной окружности на АВ или АС.

Задачи на построение технического рисунка

Как при помощи слесарного разметочного угольника измерить недоступный диаметр круглой детали.

Можно ли прибором, изображенным на рисунке одним прикладыванием найти центр круга?

«Как найти центр окружности?» — вопрос, на который мне пришлось ответить в ходе исследования. Таким образом, я нашел несколько способов построения центра окружности: 1) центроискатель — прямой угол. Принцип работы: вписанный угол опирается на диаметр. 2) Центроискатель — угол с биссектрисой. Принцип работы: диаметр окружности лежит на биссектрисе угла, описанного около этой окружности.3)Центроискатель – пара взаимно перпендикулярных прямых. Принцип работы: диаметр, проведенный в точку касания, перпендикулярен касательной. 4)Центроискатель – пара взаимно перпендикулярных прямых. Принцип работы: хорда, перпендикулярная другой хорде и проходящая через ее середину, есть диаметр.

Соответственно цель моей работы достигнута: изучив несколько способов нахождения центра окружности возможно из каждого выбрать оптимальный вариант.

О, математика земная!
Гордись, прекрасная, собой,
Ты всем наукам мать родная,
И дорожат они тобой.

Твои расчеты величаво
Ведут к планетам корабли
Не ради праздничной забавы,
А ради гордости Земли!

Список использованной литературы и источников

1.Журнал «Математика в школе» №20 1989г.

Видео:Как найти центр окружности с помощью циркуля и линейкиСкачать

Как найти центр окружности цилиндра равна

Если секущая плоскость пересекает ось цилиндра и не перпендикулярна ей, то в сечении может получиться эллипс (рис. 145) или его некоторая часть (рис. 146, 147). Это следует из того, что параллельной проекцией окружности на плоскость, не параллельную плоскости окружности, является эллипс. ( Вспомните : наклонив цилиндрический стеклянный сосуд с водой, вы видите на поверхности воды эллипс или его часть. )

Сечение цилиндра плоскостью, проходящей через ось, называется осевым сечением цилиндра. Так как поворот пространства вокруг прямой на угол 180 ° является осевой симметрией относительно оси вращения, то ось прямого кругового цилиндра является его осью симметрии. Значит, осевым сечением цилиндра вращения является прямоугольник, стороны которого равны диаметру основания и образующей цилиндра (рис. 148). При этом все осевые сечения цилиндра — равные между собой прямоугольники .

Цилиндр, осевое сечение которого — квадрат, называют равносторонним цилиндром (рис. 149).

Так как все образующие цилиндра равны и параллельны друг другу, то любое сечение цилиндра плоскостью, параллельной его оси, есть прямоугольник, высота которого равна образующей цилиндра (рис. 150).

б) Изображение цилиндра. Чтобы построить изображение цилиндра, достаточно построить: 1) прямоугольник AВB 1 A 1 и его ось OO 1 (рис. 151); 2) два равных эллипса, центрами которых являются точки O и O 1 и осями — отрезки АВ и A 1 В 1 . Выделив штрихами невидимые линии, получаем искомое изображение цилиндра.

в) Касательная плоскость к цилиндру.

Определение. Плоскость, проходящая через образующую цилиндра перпендикулярно плоскости осевого сечения, проведённой через эту образующую, называется касательной плоскостью к цилиндру (рис. 152).

Говорят, что плоскость α касается цилиндра ( цилиндрической поверхности ) по образующей DD 1 , каждая точка образующей DD 1 является точкой касания плоскости α и данного цилиндра.

Через любую точку боковой поверхности цилиндра проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности цилиндра можно провести лишь одну плоскость, касательную к данному цилиндру в этой точке.

17.3. Развёртка и площадь поверхности цилиндра

Следует заметить, что развёртка поверхности вращения — понятие в определённой мере интуитивное. К тому же не для каждой поверхности тела вращения можно построить её развёртку. Иными словами, не каждую поверхность можно «развернуть» на плоскости. Например, не существует развёртки сферы (см. раздел «Дифференциальная геометрия» в конце этой книги).

Развёртку цилиндра мы также введём на интуитивном уровне.

Пусть R — радиус основания, h — высота цилиндра.

Полная поверхность цилиндра состоит из его боковой поверхности и двух оснований — равных кругов. Если эту поверхность «разрезать» по образующей DD 1 (рис. 153) и по окружностям оснований, затем боковую поверхность развернуть на плоскости, то получим развёртку полной поверхности цилиндра (рис. 154), состоящую из прямоугольника и двух равных кругов, касающихся противоположных сторон этого прямоугольника (рис. 155).

Попробуйте изготовить развёртку цилиндра и склеить из неё цилиндр.

За площадь боковой поверхности цилиндра принимается площадь её развёртки , т. е. площадь боковой поверхности цилиндра равна площади прямоугольника, у которого одна сторона равна длине окружности основания цилиндра, а другая сторона — высоте цилиндра:

Таким образом, доказана следующая теорема.

Теорема 26. Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту. ▼

Площадь круга радиуса R равна π R 2 , поэтому S осн = π R 2 . Тогда для нахождения площади полной поверхность цилиндра справедливо:

S полн = S бок + 2 S осн = 2 π Rh + 2 π R 2 = 2 π R ( R + h ) .

Следствие. Пусть цилиндр образован вращением прямоугольника ABCD вокруг его высоты AD (рис. 156) . Тогда

S бок = 2 π DC • BC . (1)

Если EF — серединный перпендикуляр к образующей BC, проведённый из точки F оси l цилиндра, то EF = CD. Учитывая, что ВС = AD, получаем: S бок = 2 π EF • AD, т. е. боковая поверхность цилиндра равна произведению высоты цилиндра на длину окружности, радиус которой равен длине серединного перпендикуляра его образующей, проведённого из точки оcu цилиндра.

Это следствие найдёт своё применение в п. 19.7.

17 . 4 . Призмы, вписанные в цилиндр и описанные около цилиндра

Нам предстоит решать задачи, в которых рассматриваются многогранники, вписанные в фигуры вращения и описанные около них.

Для правильного и наглядного изображения конфигураций из таких многогранников и фигур вращения необходимо верно изображать правильные многоугольники, вписанные в окружность (круг) или описанные около неё.

Определение. Призма называется вписанной в цилиндр, если основания призмы вписаны в основания цилиндра (рис. 157).

Цилиндр в этом случае называют описанным около призмы.

Боковые рёбра призмы соединяют соответственные вершины её оснований, вписанных в основания цилиндра. Эти вершины лежат на окружностях оснований цилиндра. Образующие цилиндра соединяют соответственные точки окружностей его оснований и параллельны боковым рёбрам призмы. Следовательно, боковые рёбра вписанной в цилиндр призмы — образующие цилиндра.

Определение. Призма называется описанной около цилиндра, если основания призмы описаны около оснований цилиндра.

Цилиндр при этом называют вписанным в призму (рис. 158).

Так как соответственные стороны оснований призмы параллельны друг другу и перпендикулярны радиусам оснований цилиндра, проведённым в точки касания, то плоскости боковых граней призмы являются касательными плоскостями к цилиндру: эти плоскости касаются поверхности цилиндра по образующим , соединяющим точки, в которых стороны оснований призмы касаются окружностей оснований цилиндра.

При изображении правильных призм, вписанных в цилиндр, следует руководствоваться алгоритмами построений изображений правильных многоугольников, вписанных в окружность.

Итак, для построения изображения правильной призмы, вписанной в цилиндр: 1) строим изображение цилиндра; 2) строим изображение правильного многоугольника, вписанного в верхнее основание цилиндра; 3) через вершины построенного вписанного многоугольника проводим образующие цилиндра; 4) в нижнем основании цилиндра последовательно соединяем концы этих образующих; 5) выделяем видимые и невидимые линии (отрезки) изображаемых фигур.

На рисунке 159 изображены вписанные в цилиндр: призма, в основании которой прямоугольный треугольник (рис. 159, а ); правильная четырёхугольная призма (рис. 159, б ); правильная треугольная призма (рис. 159, в ); правильная шестиугольная призма (рис. 159, г ).

 ЗАДАЧА (3.029). Диагональ осевого сечения равностороннего цилиндра равна a . Найти площади боковой и полной поверхностей правильной призмы, вписанной в этот цилиндр, если призма: а) треугольная; б) четырёхугольная; в) шестиугольная.

Решени е. Рассмотрим случай а). Пусть в равносторонний цилиндр вписана правильная призма ABCA 1 B 1 C 1 (рис. 160); CDD 1 C 1 — осевое сечение; OO 1 = h — высота цилиндра; ОС = R — радиус основания цилиндра.

Так как цилиндр — равносторонний, то CDD 1 C 1 — квадрат, значит, высота цилиндра равна диаметру его основания. Тогда в квадрате СDD 1 С 1 находим CD = = a = h.

Далее, △ АВС — правильный, вписанный в основание, радиус которого R = = . Значит, сторона АВ и высота СЕ этого треугольника равны: АВ = R = , СЕ = R = a. Откуда

S осн = = ;
S бок = 3 S ABB 1 A 1 = 3 AB • BB 1 = 3 • • a = .

S полн = S бок + 2 S осн = + 2 • = .

Ответ: a) ; .

 ЗАДАЧА (3.032). В равносторонний цилиндр, высота которого равна a, вписана правильная призма. Найти расстояние и угол между диагональю боковой грани призмы и осью цилиндра, если призма: а) треугольная; б) четырёхугольная; в) шестиугольная.

Решени е. Рассмотрим случай б). Пусть ABCDA 1 B 1 C 1 D 1 — вписанная в цилиндр правильная призма (рис. 161). Найдём расстояние и угол между осью OO 1 цилиндра и скрещивающейся с ней (почему?) диагональю АB 1 боковой грани ABB 1 A 1 данной призмы.

Расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, проведёнными через эти прямые.

Если точка Е — середина отрезка AD, то расстояние между скрещивающимися прямыми AB 1 и OO 1 равно расстоянию между плоскостью грани ABB 1 A 1 и параллельной ей (почему?) плоскостью сечения EFF 1 E 1 . Это расстояние равно длине отрезка ОK (где точка K — середина АВ ), так как OK ⟂ ( ABB 1 ) и ( ABB 1 ) || ( EFF 1 ) .

Поскольку данный цилиндр — равносторонний, то BDD 1 B 1 — квадрат со стороной BD = ВВ 1 = a. Тогда АВ = = . Значит, ОK = АЕ = = — искомое расстояние между прямыми ОО 1 и АВ 1 .

Обозначим ∠ ( OO 1 ; AB 1 ) = ϕ , M = AB 1 ∩ A 1 B. Для нахождения угла ϕ проведём в грани ABB 1 A 1 прямую KK 1 || OO 1 . Тогда ϕ = ∠ ( OO 1 ; AB 1 ) = ∠ ( KK 1 ; AB 1 ) . Так как KK 1 || OO 1 , OO 1 ⟂ ( ABC ) , то MK ⟂ AB. Поэтому △ АKМ — прямоугольный. В этом треугольнике АK = , KМ = . Значит, tg ϕ = = , откуда ϕ = arctg .

Ответ: б) , arctg .

Во многих пособиях по геометрии за площадь боковой поверхности цилиндра принимают предел последовательности площадей боковых поверхностей правильных вписанных в цилиндр (или описанных около цилиндра) n- угольных призм при n → + ∞ .

Действительно, S бок. пов. призм = h • P осн. призм , где Р осн. призм — периметр основания призмы, h — длина её высоты. Для правильных вписанных в цилиндр призм h — постоянная величина, равная длине высоты цилиндра, а предел последовательности периметров правильных многоугольников, вписанных в окружность (основание цилиндра), равен длине этой окружности. Таким образом, мы вновь получаем: S бок = 2 π Rh.

17.5. Объём цилиндра

Напомним принятое нами соглашение, основанное на принципе Кавальери.

«Пусть даны два тела и плоскость. Если каждая плоскость, параллельная данной плоскости и пересекающая одно из данных тел, пересекает также и другое, причём площади сечений, образованных при пересечении обоих тел, относятся как m : n, то и объёмы этих тел относятся как m : n ».

Расположим цилиндр, имеющий высоту h и радиус основания R, и прямоугольный параллелепипед с рёбрами h, R, R так, чтобы их основания находились на двух параллельных плоскостях, расстояние между которыми равно h (рис. 162). Каждая плоскость, параллельная данным плоскостям и пересекающая цилиндр, пересекает также прямоугольный параллелепипед, причём площади образованных при пересечении обоих тел сечений относятся как π • R 2 : R 2 = π : 1. Тогда и для объёмов этих тел справедливо: V цил : V парал = π : 1 или V цил : ( R 2 • h ) = π : 1, откуда

V цил = π • R 2 • h.

Если цилиндр высотой h пересечь плоскостью, параллельной его оси, то этот цилиндр разобьётся на два тела (рис. 163). Объёмы этих тел относятся как площади сегментов, образовавшихся в основании цилиндра (докажите это на основании принципа Кавальери). Следовательно, объём каждого из этих тел может быть вычислен по формуле

Любая плоскость, проведённая через середину оси цилиндра, разбивает этот цилиндр на два равновеликих тела (рис. 164), объём V каждого из которых равен половине объёма данного цилиндра, т. е. V = π • R 2 • h.

Попробуйте, исходя из этой формулы, доказать, что в таком случае объём каждой части цилиндра (см. рис. 164) может быть вычислен по формуле:

V= π • R 2 • ( a + b ),

где a и b — длины отрезков, на которые образующая цилиндра делится секущей плоскостью.

Видео:Как выпилить идеальный круг без фрезерного циркуля Столярные урокиСкачать

Чем измеряют окружность цилиндра

Видео:Радиус и диаметрСкачать

Диаметр и высота цилиндра

Видео:Геометрия Задача найти центр круга /math and magicСкачать

Свойства

Через диаметр цилиндра можно рассчитать его радиус и периметр основания цилиндра. Радиус будет равен половине диаметра, а периметр – его произведению на число π. r=D/2 P=πD

Зная диаметр и высоту цилиндра, можно узнать площадь, объем, диагональ цилиндра и остальные параметры. Площадь боковой поверхности цилиндра представляет собой площадь прямоугольника, сторонами которого являются периметр основания цилиндра и его высота. Чтобы затем найти площадь полной поверхности цилиндра через диаметр и высоту, нужно к площади боковой поверхности добавить площадь верхнего и нижнего оснований, каждое из которых равно произведению числа π на четверть квадрата диаметра. S_(б.п.)=hP=πDh S_(п.п.)=S_(б.п.)+2S_(осн.)=πDh+(πD^2)/2=πD/2(2h+D) P=πD

Объем цилиндра представляет собой площадь его основания, умноженную на высоту. Чтобы найти объем цилиндра через диаметр и высоту, нужно умножить квадрат диаметра на четверть числа π и на высоту. V=(πD^2 h)/4 P=πD

Диагональ цилиндра находится из прямоугольного треугольника, в котором она является гипотенузой, а катеты представлены высотой и диаметром цилиндра. По теореме Пифагора диагональ цилиндра через высоту и диаметр цилиндра равна квадратному корню из суммы их квадратов. (рис. 25.1) d=√(h^2+D^2 ) P=πD

Чтобы найти радиус сферы вписанной в цилиндр, если его диаметр равен высоте, нужно разделить диаметр цилиндра либо высоту на два, так как радиус вписанной сферы равен радиусу цилиндра. (рис.25.2) r_1=h/2=D/2 P=πD

Радиус сферы, описанной вокруг цилиндра, при соблюдении тех же условий (равенство диаметра цилиндра и его высоты) равен половине диагонали цилиндра.(рис.25.3) R=d/2=√(h^2+D^2 )/2

Видео:Как найти центр кругаСкачать

Длина окружности

Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так — l

Видео:Найти центр и радиус окружностиСкачать

Как найти длину окружности через диаметр

Диаметр — отрезок, который соединяет две точки окружности и проходит через её центр. Формула длины окружности через диаметр:

π— число пи — математическая константа, равная 3,14

Видео:Окружность и круг, 6 классСкачать

Как найти длину окружности через радиус

Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:

Видео:Как найти центр и радиус нарисованной окружности #математика #егэ2023 #школа #fyp #shortsСкачать

Как вычислить длину окружности через площадь круга

Если вам известна площадь круга, вы также можете узнать длину окружности:

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Как найти длину окружности через диагональ вписанного прямоугольника

Как измерить окружность, если в нее вписан прямоугольник:

d — диагональ прямоугольника

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Как вычислить длину окружности через сторону описанного квадрата

Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:

π — математическая константа, равная 3,14

Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Как найти длину окружности через стороны и площадь вписанного треугольника

Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:

π — математическая константа, она всегда равна 3,14

a — первая сторона треугольника

b — вторая сторона треугольника

c — третья сторона треугольника

Как найти длину окружности через площадь и полупериметр описанного треугольника

Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.

Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.

π — математическая константа, равная 3,14

p — полупериметр треугольника

Как вычислить длину окружности через сторону вписанного правильного многоугольника

Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.

Формула вычисления длины окружности:

π — математическая константа, равная 3,14

a — сторона многоугольника

N — количество сторон многоугольника

Задачи для решения

Давайте тренироваться! Двигаемся от простого к сложному:

Задача 1. Найти длину окружности, диаметр которой равен 5 см.

Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:

Подставляем туда известные переменные и получается, что длина окружности равна

Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм

Решение. Радиус окружности равен Подставим туда наши переменные и получим

Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.

На спор померил диаметр вала без штангеля. Точность до десятых

Друзья, поздравляю всех с новогодними праздниками.

Поделюсь с вами хитростью, которая выручала меня не раз. Пробовали без штангенциркуля измерять диаметры? Валов, труб, шкивов? Не линейкой же это делать… хотя кто знает, может и она подойдет… А в ситуациях, когда для измерения нет доступа к торцу? Как думаете, это возможно? Конечно, да. С точностью до десятой доли миллиметра! Я даже пару раз так выигрывал спор у мужиков с горячим характером. Сейчас расскажу как.

На фото двигатель с диаметром вала 5 мм с допуском в плюс под посадку в натяг пластиковой муфты. Давайте узнаем его точный диаметр не прибегая к измерениям штангенциркулем.

Берем швейную нитку. Желательно тонкую и прочную. Делаем 10 оборотов вокруг вала, виток к витку перпендикулярно оси. Но так, чтобы они не накладывались друг на друга.

Количество витков влияет на точность измерений. Если ловить десятые доли миллиметра ни к чему, можно ограничиться одним витком.

Гелевой ручкой проводим на нитках черту вдоль оси вала. Желательно сделать это одним движением, чтобы линия оставалась тонкой.

Готово. Теперь снимаем нитку и линейкой измеряем длину 10 витков (между первой и последней чертой).

Отметки на нитке видны не очень хорошо, поэтому смотреть надо крайне внимательно. Главное не пропустить виток. Для надежности можно пересчитать отметки. Их будет одиннадцать.

В моем случае получилось 158 мм. Для пущей скрупулезности можно проинтерполировать и принять 157,8 мм. Дальше пойдет математика.

Из школьного курса помним, что длина дуги окружности — это произведение диаметра на число Пи. Соответственно, чтобы получить диаметр, нужно длину одного витка разделить на Пи. Опять же для «суперточности» возьмем число с пятью знаками после запятой.

Штангенциркуль, кстати, на этом валу показал результат 5,01 мм. Нитка ошиблась всего в одну сотую. Но это скорее повезло. Обещать точность до сотых в споре на ящик пива я бы не стал)))

На этом у меня все. Спасибо, что дочитали. Если статья оказалась полезной, подписываетесь на канал и, конечно, ставьте палец вверх 👍. Еще раз с Новым Годом! Всех благ!

Нутромер для измерения диаметра цилиндра

Вы здесь

Оглавление

Нутромер является измерительным инструментом, который предназначается для получения данных о расстоянии между двумя поверхностями, а также определения внутреннего диаметра различных деталей. В среднем, точность измерения этим прибором составляет 0,01 мм. Нутромер для измерения диаметра цилиндра состоит из сменных калиберных стержней, которые являются удлинителями и головки. Сама головка состоит из следующих частей:

• Сменный наконечник;
• Стопорное устройство;
• Стебель;
• Колпачок;
• Барабан;
• Микрометрический винт

Благодаря наличию сменных наконечников можно увеличить предел измерений. Для тех приборов, у которых точность измерения составляет 0,01 мм, актуальным ГОСТом является 868-82, а для устройств с ценой деления 0,001 или 0,002 мм – 9244-75.

Преимущества нутромеров состоят в достаточно высокой точности измерения, как для частной, так и для производственной сфере. Стоимость прибора также не высока. Главное, что здесь сохраняются преимущества всех механических устройств, куда относится долговечность работы. В то же время за ними требуется специальный уход и особые условия хранения. При поломке зачастую ремонт очень сложен и выходит легче заменить прибор на новый, чем отремонтировать. При некоторых измерениях на мягких частях могут оставаться деформации, если было сильное нажатие. Если речь идет об измерении цилиндров, то возникают сложности в местах, где имеются окна.

Какими видами нутромеров можно измерить диаметр цилиндра?

Нутромеры зачастую используется для измерения диаметра цилиндра. Для этой операции не подходят микрометры, так что специалисты используют эти разновидности устройств. Измерение цилиндров нутромером производится в двух перпендикулярных плоскостях и четырех поясах. Для этого подходят самые популярные разновидности нутромеров.

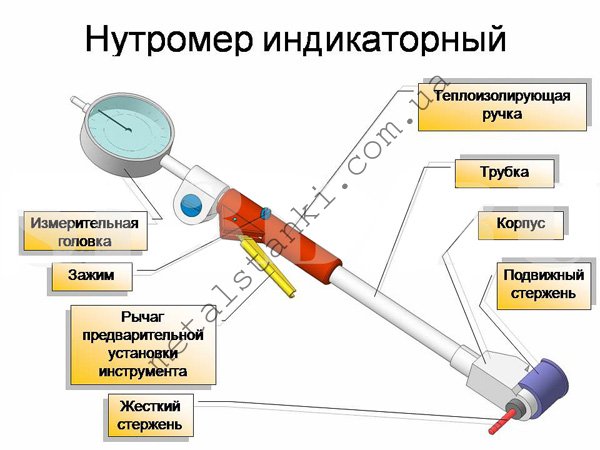
Индикаторный тип устройства подходит больше для тех цилиндров, диаметр которых является относительно небольшим. Они могут работать с размерами от 6 мм и больше. Он легко в использовании, но использует относительный метод измерения, так что у прибора имеются две шкалы. Несмотря на то, что он может работать с маленькими величинами, погрешность у него является более высокой, чем у другого типа этих устройств.

фото:нутромер индикаторный для измерения диаметра цилиндра

Микрометрический нутромер использует абсолютный способ измерения, что при той же цене деления, что и у индикаторного типа дает значительно меньшую погрешность. Предел измерений здесь лежит в диапазоне от 50 до 4000 мм, что зависит от конкретной модели. Люди нередко используют два прибора, чтобы получить более точные данные.

Подбор нутромера для измерения диаметра цилиндра

Чтобы измерить цилиндр нутромером, требуется правильно подобрать само устройство. От этого будет напрямую зависеть точность результата, а также удобство использования. В первую очередь следует определиться с подходящими размерами, так как у микрометрического и индикаторного типа слишком большой разброс по минимальному пределу. Если нужно работать с деталями диаметром до 5 см, то подойдет индикаторный нутромер, если более – микрометрический.

Далее уже нужно определяться с тем, какие сменные калиберные стержни должны идти в наборе. Они расширяют и сужают рабочий диапазон прибора, так что для получения правильных данных нужно иметь широкий запас сменных частей. Чем выше класс точности, тем меньше погрешность, так что современные высокоточные устройства позволяют получить максимально точные данные для дальнейшей работы.

Естественно, что прибор должен пройти поверку, не иметь повреждений и соответствовать принятым ГОСТам. Если есть возможность, то специалисты проводят измерение несколькими приборами одновременно.

Как пользоваться нутромером – принцип проведения измерения диаметра цилиндра

Перед тем как использовать нутромер для цилиндров, необходимо убедиться, что все его стрелки находятся в нулевой позиции. Если этого нет, то их можно отрегулировать при помощи специальных винтов, отвечающих за положение стрелок. Сложность измерения цилиндра заключается в том, что не всегда можно зафиксировать прибор, чтобы он ровно стоял и точно соответствовал требуемой горизонтали.

фото:измерения диаметра цилиндра нутромером

Деталь измеряется минимум в четырех различных местах, желательно, с одинаковой удаленностью друг от друга. Это помогает определить конусность изделия и внутренние деформации. Еще одной сложностью является невозможность измерения диаметра в тех местах, где находятся окна цилиндра. Когда инструмент доходит до них, то он попросту проваливается внутрь. В четырехтактных моторах, где в цилиндрах нет окон, таких проблем не возникает и нутромер может выполнить все необходимые функции. В ином же случае может потребоваться применение дополнительных измерительных приборов. Также можно измерять размеры в непосредственной близости от окон.

Геометрические тела. Цилиндр.

Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.

ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.

Цилиндрические сечения боковой поверхности кругового цилиндра.

Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.

Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.

Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.

Круговой цилиндр – цилиндр, основанием которого является круг.

Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.

Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.

Призма – это частный случай цилиндра.

Формулы нахождения элементов цилиндра.

Площадь боковой поверхности прямого кругового цилиндра:

Площадь полной поверхности прямого кругового цилиндра:

Объем прямого кругового цилиндра:

Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h₁ и максимальной высоты h₂.

Площадь боковой поверхности скошенного цилиндра:

Площадь оснований скошенного цилиндра:

Площадь полной поверхности скошенного цилиндра:

Объем скошенного цилиндра:

S_бок — площадь боковой поверхности;