Через точку а окружности проведены хорда ac

В окружности через середину O хорды BD проведена хорда AC так, что дуги AB и CD равны. Докажите, что O — середина хорды AC.

Вписанные углы ADB, CBD , ACB и DAC опираются на равные дуги, значит, они равны.

Получаем, что треугольники СOВ и AOD подобны по двум углам; их коэффициент подобия равен BO:OD. Поскольку BO = OD , эти треугольники равны, следовательно, AO = OC.

Видео:№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать

Через точку A лежащую на окружности, проведены диаметр AB и хорда AC, причем AC = 8 BAC = 30 Найдите ходру CM, перпендикулярную AB?

Геометрия | 10 — 11 классы

Через точку A лежащую на окружности, проведены диаметр AB и хорда AC, причем AC = 8 BAC = 30 Найдите ходру CM, перпендикулярную AB?

Рисунок нарисуйте, и все понятно будет.

Треугольник АСМ прямоугольный.

Угол СМА = 90° СМ лежит напротив угла в 30°, а значит, катет СМ равен половине гипотенузы, т.

Видео:№635. Через точку А окружности проведены касательная и хорда, равная радиусу окружности.Скачать

В окружности с центром O проведены хорды AB и CD, пересекающиеся в точке M, причем AM = 4, MB = 1, CM = 2?

В окружности с центром O проведены хорды AB и CD, пересекающиеся в точке M, причем AM = 4, MB = 1, CM = 2.

Найдите угол OMC.

Видео:№658. Через точку А к данной окружности проведены касательная АВ (В — точка касания) и секущая ADСкачать

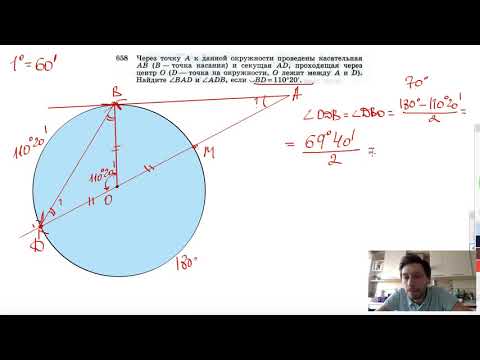
В окружности с центром О проведены диаметр АС и хорда ВD, пересикающейся в точке М, причем BM = DM?

В окружности с центром О проведены диаметр АС и хорда ВD, пересикающейся в точке М, причем BM = DM.

Угол BAC = 35градусов.

Найдите угол BAD.

Видео:№640. Даны окружность с центром О радиуса 4,5 см и точка А. Через точку А проведены две касательныеСкачать

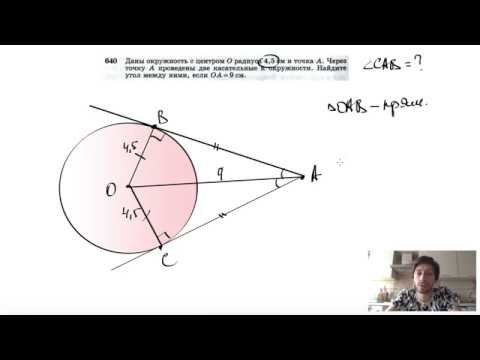
Пожалуста помогите 7 класс задачаОтрезки AB и AC — соответственно диаметр окружности и хорда окружности с центром О, хорда AC равна радиусу этой окружности?

Пожалуста помогите 7 класс задача

Отрезки AB и AC — соответственно диаметр окружности и хорда окружности с центром О, хорда AC равна радиусу этой окружности.

Найдите угол BAC.

Видео:Геометрия В окружности проведены диаметр AC и хорда AB равная радиусу окружности Найдите углыСкачать

Через точку А лежащую на окружности проведены диаметр АВ и хорда АС причем АС = 8 угол ВАС = зо гр?

Через точку А лежащую на окружности проведены диаметр АВ и хорда АС причем АС = 8 угол ВАС = зо гр.

Найдите длину хорды СМ перпендикулярной АВ.

Видео:Через точку A, лежащую вне окружности, проведены две прямые.Скачать

В окружности с центром в точке О проведены диаметр ВD и радиус ОК , причем хорда DK = OK?

В окружности с центром в точке О проведены диаметр ВD и радиус ОК , причем хорда DK = OK.

Найдите ВОК, если КDВ = 60 градусов.

Видео:Геометрия В окружности проведены хорды AB и CD, пересекающиеся в точке M. Дано: AM/МВ =5/7Скачать

Точка M отстоит от центра окружности на расстоянии 4?

Точка M отстоит от центра окружности на расстоянии 4.

Через точку M проведена хорда, перпендикулярная диаметру окружности.

Найдите длину этой хорды, если радиус окружности равен 5.

Видео:№672. Через точку А, лежащую вне окружности, проведены две секущие, одна из которых пересекаетСкачать

Через точку А, лежащую на окружности, проведены диаметр АВ и хорда АС, причём АС = √2, угол АВС = 45°?

Через точку А, лежащую на окружности, проведены диаметр АВ и хорда АС, причём АС = √2, угол АВС = 45°.

Найдите длину хорды СМ, перпендикулярной АВ.

Видео:Радиус и диаметрСкачать

Начертите окружность?

Отметьте точку на окружности.

Обозначьте ее буквой А.

Проведите хорды через точку А.

Сколько хорд можно провести?

Можно ли провести диаметр окружности через точку А?

Сколько диаметров можно провести?

Видео:№671. Через точку А проведены касательная АВ (В — точка касания) и секущая, которая пересекаетСкачать

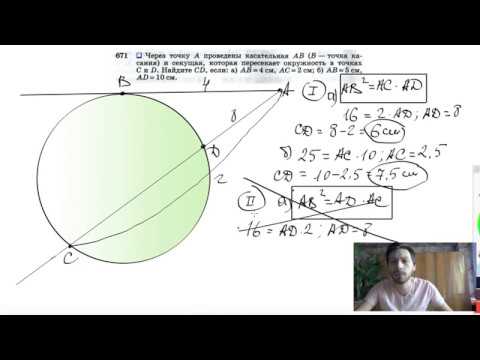
В окружности проведён диаметр AB и хорды AC и AD так, что угол BAC = BAD?

В окружности проведён диаметр AB и хорды AC и AD так, что угол BAC = BAD.

Докажите, что AC = AD.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

В окружность с центром O проведены две хорды AB и AC, причем хорда AB равна стороне правильного вписанного в эту окружность шестиугольника, а хорда AC — стороне вписанного в ту же окоужность квадрата?

В окружность с центром O проведены две хорды AB и AC, причем хорда AB равна стороне правильного вписанного в эту окружность шестиугольника, а хорда AC — стороне вписанного в ту же окоужность квадрата.

Найдите угол BAC.

На этой странице сайта размещен вопрос Через точку A лежащую на окружности, проведены диаметр AB и хорда AC, причем AC = 8 BAC = 30 Найдите ходру CM, перпендикулярную AB? из категории Геометрия с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 10 — 11 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

Площадь S = 128 Площадь CEF = Площадь BDE / 4 = S / 16 = 8 Площадь AEB = Площадь ABC / 2 = S / 4 = 32 Площадь AFD = Площадь ACD / 2 = S / 4 = 32 Площадь AEF = 128 — 32 — 32 — 8 = 56.

Номер 16 : Угол Ф = углу Л, так как в паралелограме противоположные углы равны. Далее рассмотрим треугольник КЛЕ. В нём есть две равные стороны, из чего можно сделать вывод что он равнобедренный. А так, как в равнобедренном треугольнике углы при о..

2 = 2к + в — 1. 5 = 5. 5к + в — — — — — — — — — — — — — — — — 0. 5 = — 3. 5к| : ( — 3. 5) к = — 1 / 7 2 = 2 * ( — 1 / 7) + в в = 2 + (2 / 7) в = 2 + 2 / 7.

Угол между прямыми АВ1 и СD — это∠АB₁A₁ ( CD║A₁B₁) ΔAA₁B₁ AA₁ / A₁B₁ = tgα = √3, ⇒α = ∠АB₁A₁ = π / 3.

Второстепенными членами предложения бывают : 1) ОБСТОЯТЕЛЬСТВА, они могут отвечать на вопросы КОГДА? КАК ДОЛГО? (времени), ГДЕ? ОТКУДА? КУДА? (места), КАК? КАКИМ ОБРАЗОМ? (образа действия), ИЗ — ЗА ЧЕГО? ПОЧЕМУ? (причины), С КАКОЙ ЦЕЛЬЮ? ЗА..

Прилагательное , обстоятельство места (времени ), дополнение, еще есть причастные обороты (если знаешь, что это).

Имеем трапецию АВСД. Из вершин В и С опустим перпендикуляры ВЕ и СК на АД. Из равных треугольников АВе или СКД находим высоту трапеции по Пифагору : ВЕ = √(СД² — ((АД — ВС) / 2)²) = √(5² — 3²) = √(25 — 9) = √16 = 4. Средняя линия равна (10 + 4) / ..

1) треугольник NOM — р / б Угол ONM = углу OMN = (180° — 64°) : 2 = 58° Угол NMP = 90° Угол OMP = 90° — 58° = 32°.

A = 3 см b = 16 см c = 12 см V — ? V = abc = 3 * 16 * 12 = 576 (см³) Ответ : 576 см³.

Формула объёма для куба с ребром «a» : V = a * a * a = a ^ 3.

Видео:№636. Через концы хорды АВ, равной радиусу окружности, проведены две касательные, пересекающиесяСкачать

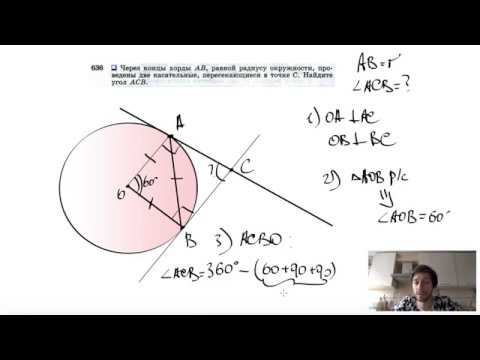
Касательная к окружности

О чем эта статья:

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Видео:Геометрия 7-8-9 класс Атанасян Номер 635Скачать

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

• окружность с центральной точкой А;
• прямая а — касательная к ней;
• радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.

Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).

Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°

🎦 Видео

Геометрия Докажите, что если через точку A к окружности проведены касательная AM (M – точка касания)Скачать

Геометрия Точка K делит хорду AC окружности пополам, а хорду DE – на отрезки длиной 2 см и 32 смСкачать

Хорды AC и BD окружности пересекаются в точке P, BP=6, CP=8, DP=12. Найдите AP.Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Геометрия В окружности проведены две хорды AB = a и AC = b. длина дуги AC вдвое больше длины дуги ABСкачать

Из точки A проведены две касательные к окружности ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать