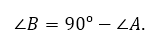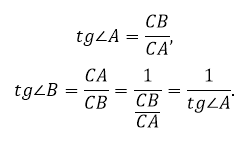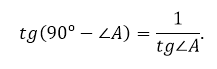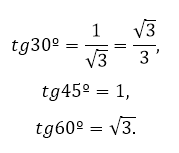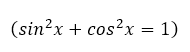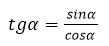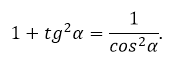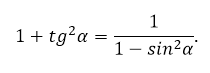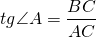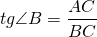Как найти тангенс треугольника авс (5 видео)

Что такое тангенс угла и как его найти

Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.

Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.

Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.

Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.

Содержание

Тангенс угла
Тангенс — это отношение.
Как найти тангенс угла (формулы)
Как найти тангенс по клеточкам
Комментарии и отзывы (5)
Тангенс в прямоугольном треугольнике
Геометрия
Основные тригонометрические функции
Взаимосвязь между тригонометрическими функциями
Тригонометрические функции стандартных углов
Поиск тангенса на квадратной решетке
🎦 Видео

Видео:ОГЭ как найти тангенс угла, если нет треугольника #математика #огэ #огэматематика #геометрияСкачать

Тангенс угла

Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.

В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.

Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса (это что?), тангенса, котангенса.

Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.

Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.

Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.

Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Тангенс — это отношение.

Итак, есть два определения:

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.

Тангенс – это отношение синуса к косинусу.

Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.

» alt=»»>

Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan⁡(α).

Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Как найти тангенс угла (формулы)

Первое свойство тангенса вытекает из его определения как отношения катетов.

Сумма двух непрямых углов прямоугольного треугольника равна 90º. Поэтому

Так как тангенс – это отношение катетов, то

Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.

Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.

Видео:Найдите тангенс (tg(c)) угла С прямоугольного треугольника АВССкачать

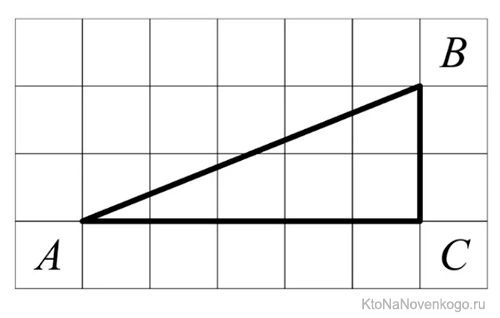
Как найти тангенс по клеточкам

Учитывая первое определение, можно определить, как найти тангенс угла по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.

Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:

Из формулы тангенсов, записывающей кратко второе определение

и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.

Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится зависимость тангенса и косинуса:

Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом:

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (5)

Я Очень Люблю Правила, Теоремы, Формулы по Предмету «Математика», «Алгебра».

Прочитал статью и остался один главный вопрос, а собственно без вспомогательных таблиц найти угол В ГРАДУСАХ вообще возможно и есть ли у вас статья, где рассказыввается как это сделать? Спасибо.

Я ни разу не математик, но почему у вас сумма углов прямоугольного треугольника равна 90 градусов. А так все хорошо начиналось. Объясняете хорошо, но после таких ошибок у меня сомнения что информация верная.

Спасибо. Уточнил в тексте, что это сумма двух непрямых углов прямоугольного треугольника.

Пишу стихи. Востребован тангенс для решения жизненных ситуаций поскольку состоит из тех же функций,как-то, касающийся,прилежащий, трогающий. Куда без них денешься.

Видео:В треугольнике ABC угол C равен 90°, AB = 13, тангенс A = 1/5. Найдите высоту CH.Скачать

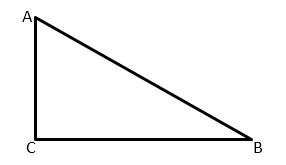
Тангенс в прямоугольном треугольнике

Что такое тангенс в прямоугольном треугольнике? Как найти тангенс? От чего зависит значение тангенса?

Например, для угла A треугольника ABC

Поэтому тангенс угла A в треугольнике ABC — это

Для угла B треугольника ABC

противолежащим является катет AC,

Соответственно, тангенс угла B в треугольнике ABC

равен отношению AC к BC:

Таким образом, тангенс острого угла прямоугольного треугольника — это некоторое число, получаемое при делении длины противолежащего катета на длину прилежащего катета.

Так как длины катетов — положительные числа, то и тангенс острого угла прямоугольного треугольника является положительным числом.

Тангенс угла треугольника зависит от величины угла, но не зависит от катетов (важно лишь их отношение).

Если в треугольнике изменить длины катетов, не меняя угол, то величина тангенса не изменится.

Видео:ОГЭ математика ФИГУРЫ НА РЕШЕТКЕ 19#1🔴Скачать

Геометрия

План урока:

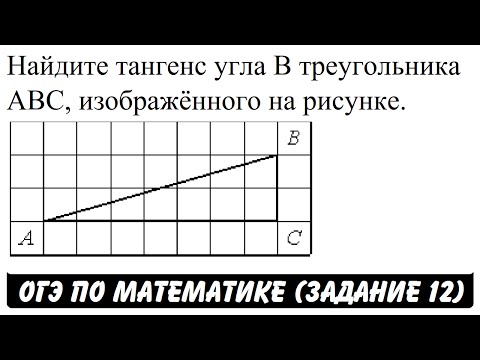
Видео:Найдите тангенс угла B треугольника ABС | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

Основные тригонометрические функции

Пусть есть некоторый прямоугольный треугольник АBС, у которого∠С = 90°. Обозначим какой-нибудь его острый угол, например, ∠А, греческой буквой α. В треугольнике есть два катета. Тот из них, который, непосредственно является одной из сторон угла α, называют прилежащим катетом. Другой катет именуют противолежащим. Ещё одна сторона треугольника – это гипотенуза, для которой не надо уточнять, прилежащая она или противолежащая относительно острого угла:

Отношения этих трех сторон друг к другу имеют особое наименование.

Для обозначения этих трех величин (их именуют тригонометрическими функциями) используют сокращения sin, cos и tg. При этом после этого сокращения может писаться как обозначение угла греческой буквой, так и обычное обозначение с помощью больших латинских букв:

Задание. Найдите значения тригонометрических функций для∠А в ∆АBС, длины сторон которого указаны на рисунке:

Решение. Просто пользуемся определениями каждой функции:

Задание. Найдите величину тригонометрических функций угла∠В в ∆АBС, показанном на рисунке:

Решение. На первый взгляд кажется, что задание повторяет предыдущее, но это не так. В данном случае нам надо вычислять функции не для∠А, а для ∠В. Для него противолежащим катетом уже будет АС, а прилежащим – ВС. Тогда можно записать, что

Задание. В прямоугольном ∆АBС гипотенуза АB имеет длину 10, а sin∠A = 0,2. Найдите величину ВС.

Решение. Запишем синус как отношение двух сторон:

Задание. В прямоугольном ∆АBС АС = 8, cos∠A = 0,4. Какова длина гипотенузы АB?

Решение. Выразим известный нам косинус как отношение двух отрезков:

Принципиально важно то, что если в двух прямоугольных треугольниках острые углы одинаковы, то и значение их синусов, косинусов и тангенсов также будут одинаковы. Действительно, пусть у ∆АBС и ∆А₁В₁С₁ одинаковы∠А и ∠А₁, а ∠С и ∠С₁ – прямые:

Тогда у них совпадает по два угла, а это означает, что ∆АBС и ∆А₁В₁С₁ подобны. Из этого подобия вытекает пропорция:

Отсюда можно сделать вывод:

Другими словами, значение тригонометрической функции угла зависит только от величины угла (его градусной меры) и НЕ зависит от того, в каком прямоугольном треугольнике этот угол построен. Действительно, с помощью калькулятора или компьютера можно всегда посчитать синус для какого-то угла, если известна его величина в градусах.

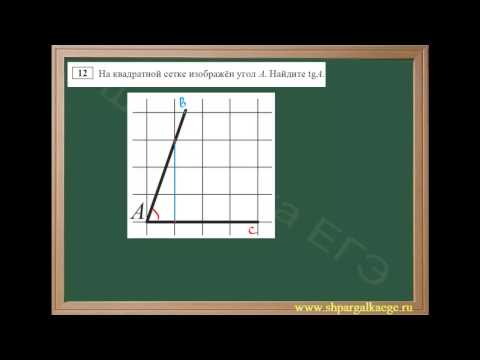
Задание. Найдите тангенс угла, изображенного на рисунке:

Решение. Нам надо самостоятельно достроить угол до прямоугольного треугольника. Удобней всего просто построить вертикальную линию, длину которой будет удобно измерить с помощью клеточек. Например, можно сделать такое построение:

Тогда тангенс можно получить, поделив вертикальный отрезок (он здесь оказывается противолежащим катетом) на горизонтальный:

Заметим, что мы могли построить и треугольник с другими размерами, однако во всех случаях величина тангенса будет одной и той же:

Задание. Постройте такой угол, что его тангенс будет равен 1,5.

Решение. Если тангенс равен 1,5, то это означает, что противолежащий катет в 1,5 раза длиннее прилежащего катета треугольника. В 1,5 раза отличаются, например, числа 2 и 3. Значит, если мы построим треугольник с катетами 2 и 3, то мы получим необходимый нам угол:

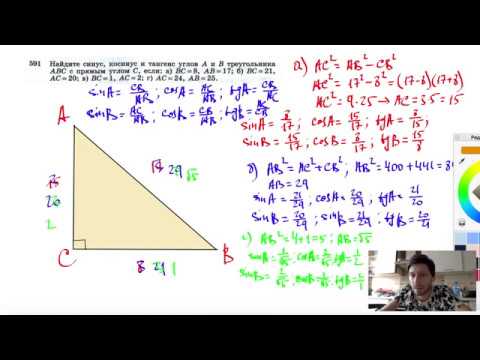
Видео:№591. Найдите синус, косинус и тангенс углов А и В треугольника ABC с прямым углом ССкачать

Взаимосвязь между тригонометрическими функциями

Оказывается, что одну тригонометрическую функцию угла, например, синус, можно найти и все остальные функции, используя буквально две формулы. Для их вывода снова построим прямоугольный ∆АBС и обозначим его∠А как α:

Запишем для α все 3 тригонометрические функции:

Для вывода второй важной формулы возведем синус и косинус в квадрат, а потом сложим их:

В итоге у нас получилось так называемое основное тригонометрическое тождество:

Задание. Известно, что синус некоторого угла в прямоугольном треугольнике составляет 0,6. Найдите его косинус и тангенс.

Решение. Обозначим этот угол как α. По условию sin α = 0,6. С помощью основного тригонометрического тождества находим косинус:

имеет не одно, а два решения: 0,8 и (– 0,8). Однако понятно, что так как все длины в геометрии – это положительные числа, то и их отношение также должно быть положительным. Поэтому в прямоугольном треугольнике тригонометрические функции могут быть только положительными, и корень (– 0,8) можно отбросить.

Далее находим тангенс:

Задание. Известен косинус острого угла, который равен 7/25. Вычислите синус и тангенс угла.

Решение. Сначала определяем синус угла:

Задание. Известен тангенс острого угла, он составляет 15/8. Найдите синус и косинус угла.

Решение. Данная задача сложнее двух предыдущих, так как две известные нам тригонометрические формулы не позволяют сразу по тангенсу вычислить две другие функции. Сначала используем формулу, в которой тангенс вообще присутствует:

Мы смогли выразить синус через косинус. Теперь можно использовать и вторую формулу:

Теперь можно вычислить и синус:

Заметим важное обстоятельство – так как гипотенуза всегда длиннее катетов, то и синус с косинусом в прямоугольном треугольнике всегда меньше единицы. На тангенс же подобных ограничений нет.

Задание. В прямоугольном ∆АBС гипотенуза АB равна 20, а cos∠A = 0,8. Вычислите длину ВС.

Решение. Если бы нам был дан синус, мы могли бы сразу найти ВС, но нам известен косинус. Здесь можно предложить два алгоритма решения задачи. Первый метод заключается в том, что мы сначала находим синус, пользуясь тригонометрическими формулами:

Второй метод решения задачи заключается в том, что сначала с помощью косинуса найти неизвестный катет АС:

Видео:Как просто запомнить, что такое sin, cos, tg?! #косинус #синус #тангенс #математика #огэ #егэСкачать

Тригонометрические функции стандартных углов

Итак, мы выяснили, что тригонометрические функции зависят от градусной меры угла. Попытаемся вычислить их для некоторых стандартных значений.

Начнем с угла в 30°. Построим прямоугольный ∆АBС с∠А = 30°:

Ещё из 7-ого класса нам известно, что в таком треугольнике гипотенуза вдвое длиннее, чем катет, лежащий напротив угла в 30°:

Далее можно найти и тангенс 30°:

Вернемся к рассматриваемому нами ∆АBС, в котором∠А = 30°. Ясно, что другой его острый угол, ∠В, будет составлять 90 – 30 = 60°:

Снова используем тот факт, что гипотенуза АB будет длиннее катета ВС в 2 раза:

Ещё один стандартный угол, для которого легко можно рассчитать значение его тригонометрических функций – это 45°. Рассмотрим прямоугольный ∆АBС, в котором один из острых углов составляет 45°. Тогда и другой острый угол должен также составлять 45°, ведь их сумма в прямоугольном треугольнике равна 90°:

Но если в треугольнике 2 угла одинаковы, то он – равнобедренный, то есть катеты АС и ВС равны:

Итак, в результате нам удалось получить 9 стандартных значений, которые можно представить в виде единой таблицы тригонометрических функций:

Задание. Составьте формулу для вычисления площади прямоугольного треугольника, если известен один из его катетов (он равен a) и острый угол, прилегающий к этому катету (он обозначается как α). Далее найдите c помощью формулы площадь треугольника, если а = 5 и α = 45°.

Решение. Как известно, площадь прямоугольного треугольника рассчитывается по формуле:

Задание. В прямоугольном ∆АBС к гипотенузе ВС проведена высота АН. Отрезок НВ имеет длину 16. Известно, что sinα = 0,6. Какова длина СН?

Решение. Сначала, зная sinα, найдем сosα и tgα:

Теперь заметим, что на рисунке угол α – это не только ∠АBС. Действительно, в ∆АBС

Нам известен отрезок АН и tg∠САН, поэтому можно найти СН:

Видео:Задача 6 №27357 ЕГЭ по математике. Урок 46Скачать

Поиск тангенса на квадратной решетке

Рассмотрим задание, которое часто встречается на экзаменах и вызывает большие затруднения. На рисунке показан угол, требуется высчитать его тангенс:

Ясно, что для нахождения тангенса надо построить какой-нибудь прямоугольный треугольник, однако проблема заключается в том, что обе стороны угла не являются ни горизонтальными, ни вертикальными линиями, а потому провести к ним перпендикуляр у многих не получается. Рассмотрим, как это делается.

Посмотрим на нижнюю линию. Она представляет собой поднимающуюся прямую, причем на каждые 2 клеточки, которые эта прямая проходит вправо, приходится подъем на 1 клеточку вверх.

Оказывается, что для построения перпендикуляра к ней необходимо от какой-нибудь ее точки вести наклонную прямую, у которой, наоборот, на каждые две клеточки подъема будет приходиться 1 клетка движения вбок, причем не вправо, а влево:

Теперь, чтобы найти тангенс, надо просто поделить длину красного отрезка (он здесь оказывается противолежащим катетом) на длину зеленого отрезка. Несложно заметить, что эти отрезки одинаковы, так как являются гипотенузами в двух равных прямоугольных ∆АBС и ∆CDF:

Естественно, что отношение одинаковых отрезков равно единице, поэтому и тангенс также равен единице. Заметим, что прямой угол можно было получить, проведя перпендикуляр к нижней линии в другой точке:

Более того, перпендикуляр можно провести и к верхней стороне угла. Она представляет собой линию, которая поднимается вправо, и на каждые три клетки движения вверх приходится одна клетка смещения вправо:

Соответственно, чтобы построить к ней перпендикуляр, надо от одной из ее точек начать двигаться вправо и вниз, причем на 3 клетки движения вбок будет приходиться только 1 клетка движения вниз:

Во всех этих случаях зеленые и красные отрезки одинаковы, а потому тангенс равен единице.

Объясним, почему для построения перпендикуляра надо использовать именно такой метод. Пусть на квадратной решетке начерчена прямая АС, к которой надо провести перпендикуляр. Построив горизонтальную (показана зеленым цветом) линию АB и вертикальную (показана красным) линию ВС, мы достоим ее до прямоугольного ∆АBС. Далее отложим от точки С уже вертикально отрезок CD, равный АB, а далее от D – горизонтальный отрезок, равный ВС:

Обозначим∠А как α, тогда ∠АСВ будет составлять 90° – α. Заметим, что ∆АBС и ∆СDF – равные, так как они прямоугольные и у них одинаковы катеты:

Теперь обратим внимание на три угла, вершины которых лежат в точке С. Это ∠АСВ, ∠FCD и ∠АСF. Они вместе образуют развернутый угол ВСD, то есть их сумма составляет 180°. Но ∠АСВ и ∠FCD мы уже выразили через величину α. Тогда можно вычислить и третий угол ∠АСF:

Получили, что отрезки АС и СF действительно перпендикулярны.

Задание. Найдите тангенс угла, показанного на рисунке:

Решение. Если попытаться провести прямую, перпендикулярную нижней стороне угла, то в результате этот перпендикуляр просто не пересечется со второй стороной:

Поэтому перпендикуляр следует проводить к верхней стороне:

Теперь осталось найти отношение длин красного (здесь это противолежащий катет) зеленого отрезка. Конечно, и длины можно найти по теореме Пифагора, однако есть и более простой метод. Возьмем в качестве единичного отрезок, который получается, если на квадратной решетке сделать два шага вбок и один вверх. Этот отрезок будет укладываться на красном катете ровно 3 раза, а на зеленом – ровно 2 раза, то есть прилежащий катет равен трем единичным отрезкам, а противолежащий – двум. Тогда их отношение составляет 3/2 = 1,5