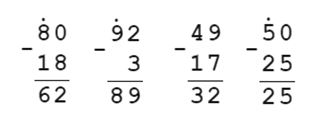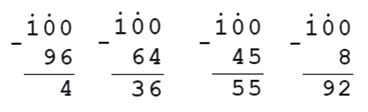Даны две пересекающиеся окружности разных радиусов постройте отрезок

Видео:Внешнее сопряжение дуги и прямой дугой заданного радиуса. Урок16.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Глава 5. Окружность
Ответы к параграфу 5.1 Окружность и прямая

Задание № 408

Что можно сказать о взаимном расположении прямой и окружности, если расстояние от центра окружности до прямой равно 4 см, а радиус окружности равен:
а) 3 см;
б) 4 см;
в) 6 см?
Подсказка. Сделайте схематический рисунок.

а) Прямая и окружность не имеют общих точек.

б) Прямая и окружность касаются друг друга.

в) Прямая и окружность пересекаются.

Задание № 409

Начертите произвольную окружность и отметьте на ней точку A. Постройте касательную к окружности в точке A.

Задание № 410

К окружности, радиус которой равен 6 см, проведены две параллельные касательные (рис. 5.3). Чему равно расстояние между ними?

6 + 6 = 12 (см) − расстояние между касательными.
Ответ: 12 см.

Задание № 411

Начертите две параллельные прямые. Постройте какую−нибудь окружность, для которой эти прямые являются касательными. Сколько таких окружностей можно построить? Где лежат их центры?

Окружностей можно построить множество. Центры этих окружностей лежат на прямой, параллельной данным и равноудаленной от них.

Задание № 412

Прямая k и окружность пересекается в точках A и B. Прямая k перемещается к центру окружности параллельно самой себе. В какой момент длина отрезка AB будет наибольшей? Сделайте соответствующий рисунок.

Длина отрезка AB будет наибольшей, когда прямая k проходит через центр окружности. В этом случае отрезок AB будет являться диаметром окружности.

Задание № 413

Проведите прямую и постройте какую−нибудь окружность радиусом 3 см, для которой эта прямая являются касательной. Сколько таких окружностей можно построить? Где расположены их центры?

Можно построить бесконечное множество таких окружностей. Их центры будут лежать по обе стороны от данной прямой на прямых, параллельных данной, на расстоянии, равному радиусу окружности 3 см.

Задание № 414

Проведите прямую и отметьте на ней произвольную точку M. Постройте несколько окружностей разных радиусов, касающихся данной прямой в точке M. Где лежат центры всех таких окружностей?

Центры окружностей лежат на прямой, перпендикулярной данной прямой.

Задание № 415

Начертите в тетради квадрат со стороной 8 см. Постройте окружность, касающуюся всех сторон квадрата.

Задание № 416

Представьте данное число в виде произведения двух десятичных дробей (укажите два решения):
а) 0,12;
б) 0,064;
в) 0,0002;
г) 0,3.

б) 0,064 = 0,4 * 0,16 = 0,8 * 0,08

в) 0,0002 = 0,1 * 0,002 = 0,001 * 0,2

Задание № 417

Найдите значение каждого из выражений:
1) 25 − 3,6 * 1,5 + 2,5;
2) (25 − 3,6) * (1,5 + 2,5);
3) 25 − 3,6 * (1,5 + 2,5).

Задание № 418

1) В полиэтиленовый пакет, выдерживающий 5 кг, положили 1,8 кг огурцов, а яблок в 1,5 раза больше. Не порвется ли пакет?
2) Представьте, что вы хотите помочь бабушке подготовить материал для изготовления шерстяного ковра из ниток разного цвета. Чтобы получить нужный узор, 1/10 всех ниток должна быть красного цвета, 2/5 − синего, 3/20 − коричневого, остальные − белого. У бабушки имеется 700 г ниток белого цвета. Рассчитайте, сколько граммов ниток каждого цвета надо взять для выполнения работы.

Видео:Окружность данного радиуса, проходящей через две заданные точкиСкачать

Даны две пересекающиеся окружности разных радиусов постройте отрезок

§ 23. Метод геометрических мест точек в задачах на построение

Известно, что если смешать синий и жёлтый цвета, то получим зелёный.

Пусть на плоскости надо найти точки, обладающие какими-то двумя свойствами одновременно. Если синим цветом покрасить точки, обладающие первым свойством, а жёлтым — обладающие вторым свойством, то понятно, что зелёные точки будут обладать сразу двумя свойствами. В этом и состоит идея метода ГМТ, которую проиллюстрируем следующими задачами.

Задача 1. Постройте треугольник по трём данным его сторонам.

Решение. Пусть даны три отрезка, длины которых равны a , b , c (рис. 327). Надо построить треугольник ABC , в котором AB = c , AC = b , BC = a .

Проведём произвольную прямую. С помощью циркуля отложим на ней отрезок CB , равный a (рис. 328). Понятно, что задача свелась к построению третьей вершины треугольника, точки A .

Воспользуемся тем, что точка A обладает сразу двумя свойствами:

1) принадлежит геометрическому месту точек, удалённых от точки B на расстояние c , т. е. окружности с центром в точке B радиуса с (см. рис. 328);

2) принадлежит геометрическому месту точек, равноудалённых от точки C на расстояние b , т. е. окружности с центром в точке С радиуса b (см. рис. 328).

В качестве точки A можно выбрать любую из двух образовавшихся зелёных точек.

Полученный треугольник ABC является искомым, так как в нём AB = c , AC = b , BC = a .

Из описанного построения следует, что если каждый из трёх данных отрезков меньше суммы двух других, то эти отрезки могут служить сторонами треугольника.

Задача 2. Постройте фигуру, все точки которой принадлежат данному углу, равноудалены от его сторон и находятся на заданном расстоянии a от его вершины.

Решение. Искомые точки принадлежат сразу двум геометрическим местам точек: биссектрисе данного угла и окружности с центром в его вершине и радиусом, равным a .

Построим биссектрису угла и указанную окружность (рис. 329). Их пересечением является искомая точка X .

Задача 3. Постройте центр окружности радиуса R , проходящей через данную точку M и касающуюся данной прямой a .

Решение. Поскольку окружность касается прямой a , то её центр находится на расстоянии R от этой прямой. Геометрическим местом точек, удалённых от данной прямой на данное расстояние, являются две параллельные прямые (см. упражнение 498). Следовательно, центр окружности находится на прямой b или на прямой с (рис. 330).

Геометрическое место точек, являющихся центрами окружностей радиуса R , проходящих через точку M , — это окружность данного радиуса с центром в точке M . Поэтому в качестве центра искомой окружности можно выбрать любую из точек пересечения окружности с одной из прямых b или с (рис. 331).

Построение для случая, когда данная точка принадлежит данной прямой, рассмотрите самостоятельно.

Задача 4. Постройте треугольник по стороне, медиане, проведённой к этой стороне, и радиусу описанной окружности.

Решение. Построим окружность данного радиуса и проведём хорду AB , равную стороне искомого треугольника. Тогда концы хорды являются двумя вершинами искомого треугольника. Понятно, что третья вершина принадлежит одновременно построенной окружности и окружности с центром в точке O , являющейся серединой хорды AB , и радиусом, равным данной медиане. Каждый из треугольников ABС 1 и ABС 2 (рис. 332) является искомым. Поскольку эти треугольники равны, то задача имеет единственное решение.

622. Даны прямая m и точки A и B вне её (рис. 333). Постройте на прямой m точку, равноудалённую от точек A и B .

623. Точки A и B принадлежат прямой m . Постройте точку, удалённую от прямой m на расстояние a и равноудалённую от точек A и B . Сколько решений имеет задача?

624. Точки B и C принадлежат разным сторонам угла A , причём АВ ≠ АС . Постройте точку M , принадлежащую углу, равноудалённую от его сторон и такую, что MB = MC .

625. Точки B и C принадлежат разным сторонам угла A . Постройте точку D , принадлежащую углу, равноудалённую от его сторон и такую, что DC = BC . Сколько решений может иметь задача?

626. Постройте равнобедренный треугольник по основанию и боковой стороне.

627. Для данной окружности постройте точку, являющуюся её центром.

628. Постройте окружность данного радиуса, проходящую через данную точку, центр которой принадлежит данной прямой.

629. Постройте окружность данного радиуса, проходящую через две данные точки.

630. Найдите все точки, принадлежащие данной окружности и равноудалённые от концов данного отрезка. Сколько решений может иметь задача?

631. Даны две пересекающиеся прямые m и n и отрезок AB . Постройте на прямой m точку, удалённую от прямой n на расстояние AB . Сколько решений имеет задача?

632. В треугольнике ABC известно, что ∠ C = 90°. На катете AC постройте точку D , удалённую от прямой AB на расстояние CD .

633. Постройте равнобедренный треугольник по основанию и радиусу описанной окружности. Сколько решений может иметь задача?

634. Постройте треугольник по двум сторонам и медиане, проведённой к одной из данных сторон.

635. Постройте равнобедренный треугольник по боковой стороне и медиане, проведённой к боковой стороне.

636. На данной окружности постройте точку, находящуюся на данном расстоянии от данной прямой. Сколько решений может иметь задача?

637. На данной окружности постройте точку, равноудалённую от двух данных пересекающихся прямых. Сколько решений может иметь задача?

638. Между двумя параллельными прямыми дана точка. Постройте окружность, проходящую через эту точку и касающуюся данных прямых. Сколько решений имеет задача?

639. Постройте окружность, проходящую через данную точку A и касающуюся данной прямой m в данной точке B .

640. Даны две параллельные прямые и секущая. Постройте окружность, касающуюся этих трёх прямых.

641. Постройте треугольник по двум сторонам и радиусу описанной окружности. Сколько решений может иметь задача?

642. Постройте треугольник по стороне, высоте, проведённой к этой стороне, и радиусу описанной окружности. Сколько решений может иметь задача?

643. Постройте равносторонний треугольник по радиусу описанной окружности.

644. Три прямые попарно пересекаются и не проходят через одну точку. Постройте точку, равноудалённую от всех трёх прямых. Сколько решений имеет задача?

645. Постройте прямоугольный треугольник по катету и сумме гипотенузы и другого катета.

646. Постройте прямоугольный треугольник по гипотенузе и сумме катетов.

647. Постройте прямоугольный треугольник по гипотенузе и разности катетов.

648. Постройте прямоугольный треугольник по катету и разности гипотенузы и другого катета.

649. Постройте равнобедренный треугольник по основанию и разности боковой стороны и высоты, опущенной на основание.

650. Постройте треугольник по стороне, прилежащему к ней углу и сумме двух других сторон.

651. Постройте треугольник по стороне, прилежащему к ней углу и разности двух других сторон.

652. Постройте треугольник по стороне, противолежащему ей углу и разности двух других сторон.

653. Постройте треугольник по стороне, противолежащему ей углу и сумме двух других сторон.

654. Постройте треугольник по стороне, разности углов, прилежащих к этой стороне, и сумме двух других сторон.

655. Постройте треугольник по периметру и двум углам.

656. Постройте остроугольный треугольник по периметру, одному из углов и высоте, проведённой из вершины другого угла.

657. Постройте треугольник по высоте и медиане, проведённым из одной вершины, и радиусу описанной окружности.

658. Постройте треугольник по двум сторонам и медиане, проведённой к третьей стороне.

659. Постройте треугольник по стороне, высоте, проведённой к этой стороне, и медиане, проведённой к одной из двух других сторон.

Упражнения для повторения

660. На рисунке 334 ∠ A = 46°, ∠ ACB = 68°, ∠ DEC = 120°. Найдите углы треугольников EFC и DBE .

661. Через середину O стороны MK треугольника MKN провели прямую, перпендикулярную стороне MK и пересекающую сторону MN в точке C . Известно, что MC = KN , ∠ N = 50°. Найдите угол MCO .

662. В треугольнике ABC из вершины прямого угла C провели высоту CH и биссектрису CM . Длина отрезка HM в 2 раза меньше длины отрезка CM . Найдите острые углы треугольника ABC .

663. На рисунке 335 BD = DC , DN ⊥ BC , ∠ BDM = ∠ MDA . Найдите сумму углов MBN и BMD .

Наблюдайте, рисуйте, конструируйте, фантазируйте

664. Разрежьте фигуру, изображённую на рисунке 336, на три части, не являющиеся квадратами, так, чтобы из этих частей можно было сложить квадрат.

Когда сделаны уроки

Из истории геометрических построений

Умение достигать результат, используя минимальные средства, всегда считалось признаком высокого мастерства. Видимо, поэтому в Древней Греции в значительной степени было развито искусство выполнять геометрические построения с помощью только двух инструментов: дощечки с ровным краем (линейки) и двух заострённых палочек, связанных на одном конце (циркуля). Такое ограничение в выборе инструментов историки связывают с древнегреческой традицией, считавшей прямую и окружность самыми гармоничными фигурами. Так, в своей книге «Начала» великий учёный Евклид описывал построения геометрических фигур, при которых использовались лишь циркуль и линейка.

Существует много задач на построение. С некоторыми из них вы уже успели познакомиться. Однако есть три задачи на построение, которые сыграли в развитии математики особую роль. Эти задачи стали знаменитыми.

Задача о квадратуре круга. Построить квадрат, площадь которого равна площади данного круга.

Задача о трисекции угла (от латинских tria — «три» и section — «разрезание») . Разделить угол на три равные части.

Задача об удвоении куба. Построить куб, объём которого в 2 раза больше объёма данного куба.

Эти задачи занимали умы людей на протяжении тысячелетий. Их пытались решить и такие выдающиеся учёные древности, как Гиппократ Хиосский, Евдокс Книдский, Евклид, Эратосфен, Аполлоний Пергский, Герон, Папп, Платон, Архимед, и гении Нового времени Рене Декарт, Франсуа Виет, Исаак Ньютон. И лишь в середине XIX века была доказана их неразрешимость, т. е. невозможность выполнить указанные построения с использованием лишь циркуля и линейки. Этот результат был получен средствами не геометрии, а алгебры, благодаря переводу этих задач на язык уравнений.

Когда вы решали задачи на построение, особенно те, которые отмечены знаком , вы, по-видимому, испытали сложности, связанные с ограниченностью набора инструментов. Поэтому предложение ещё больше сузить возможности применяемых приборов может показаться вам по меньшей мере неожиданным. Однако ещё в Х веке персидский математик Мохаммед Абу-ль-Вефа описал решение целого ряда задач на построение с помощью линейки и циркуля, раствор которого нельзя было менять. Совсем удивительной является теорема, опубликованная в 1797 году итальянским математиком Лоренцо Маскерони (1750–1800): всякое построение, выполнимое циркулем и линейкой, можно проделать одним циркулем. При этом Маскерони обусловливал следующее: поскольку одним циркулем провести прямую нельзя, то прямая считается построенной, если построены какие-нибудь две её точки.

В ХХ веке была обнаружена книга датского учёного Георга Мора (1640–1697), в которой он также описал построения одним циркулем. Поэтому сформулированную выше теорему называют теоремой Мора — Маскерони.

Видео:Радиус и диаметрСкачать

ГДЗ по математике 2 класс учебник Рудницкая, Юдачева часть 1 Страница 87-92

Страница 87

1. Какие предметы, изображённые на рисунке, в действительности похожи на окружность, а какие — на круг?
Ответ:
На окружность похожи: 1 рисунок (тигр, который прыгает через кольцо) и 3 рисунок (обруч).
На круг похожи: 2 рисунок (леденец) и 4 рисунок (солнце).

2. Используя циркуль, начерти три разные окружности. Перед выполнением задания обдумай план его выполнения. Обязательно ли надо отмечать три разных центра окружностей?
Ответ:
Необязательно отмечать три разных центра окружностей, можно провести три окружности из одного центра.
1. Нужно отметить центр окружности — точку O.
2. Выбрать любую точку A.
3. Одну ножку циркуля поставить в центр окружности, а вторую ножку, которой будете чертить, установить в точке A и начертить окружность.
Для второй и третьей окружности нужно сделать те же самые действия, кроме первого пункта.

3. Начерти окружность и проведи три её радиуса. Сколько радиусов можно провести в одной окружности?
Ответ:

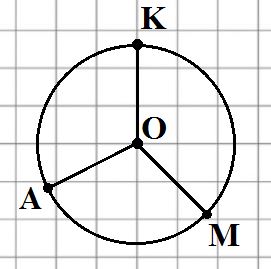
В одной окружности можно провести бесконечное множество радиусов.

Страница 88

4. Начерти с помощью циркуля окружность с центром в точке О и радиусом длиной 5 см.
Ответ:
Нужно отметить центр окружности — точку O.
Провести отрезок OA, который равен радиусу.
Одну ножку циркуля поставить в центр окружности, а вторую ножку, которой будете чертить, установить в точке A и начертить окружность.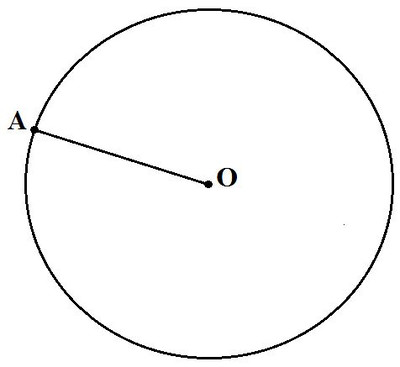

OA = 5 см

5. Начерти окружность с радиусом длиной 2 см. Начерти другую окружность с тем же центром и радиусом длиной 4 см.
Ответ: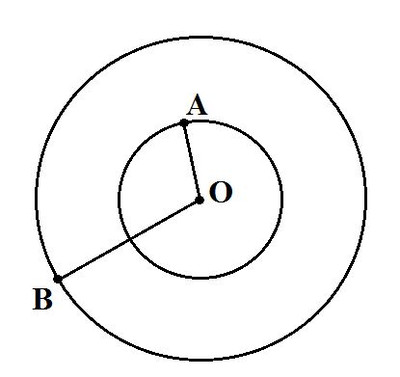

OA = 2 см
OB = 4 см

6. Сравни окружность и круг. В чём их сходство и различие?
Ответ:
Различие: Окружность — это замкнутая линия. А круг — это фигура, которая ограничена окружностью.
Сходства: Круг и окружность имеют радиус и диаметр.

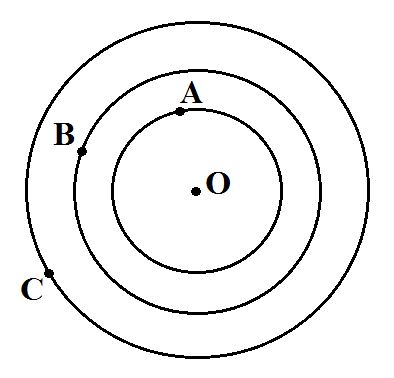
7. Начерти две разные окружности, имеющие один и тот же радиус.
Ответ: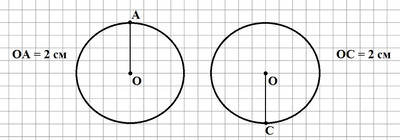

Две разные окружности OA и OC имеют один и тот же радиус, который равен 2 см.

8. Сколько окружностей ты видишь на каждом рисунке? Выбери правильный ответ.
Ответ:
На первом рисунке 6 окружностей, а на втором — 10 окружностей.

Страница 89

9. Вычисли.
(80 — 7) + 13
52 — (6 + 18)
(60 + 8) — 19
40 — (21 — 7)
Ответ:

10. Называйте по очереди ответы примеров. Если необходимо, исправляйте ошибки друг друга.
4 + 5 19 — 6 30 — 20 50 + 0
9 — 6 8 + 8 30 + 20 48 — 0
7 + 7 9 + 9 60 — 60 10 + 10
7 — 7 0 — 0 60 + 30 48 — 48
Ответ:
4 + 5 = 9
9 — 6 = 3
7 + 7 = 14
7 — 7 = 0
19 — 6 = 13
8 + 8 = 16
9 + 9 = 18
0 — 0 = 0
30 — 20 = 10
30 + 20 = 50
60 — 60 = 0
60 + 30 = 90
50 + 0 = 50
48 — 0 = 48
10 + 10 = 20
48 — 48 = 0

11. Вычисли периметр треугольника, длины сторон которого равны 2 дм 6 см, 5 дм, 3 дм 8 см.
Ответ:
Чтобы проще было считать, можно длины перевести в одинаковые единицы измерения:
2 дм 6 см = 26 см
5 дм = 50 см
3 дм 8 см = 38 см
26 см + 50 см + 38 см = 114 см = 11 дм 4 см

12. Какие из утверждений неверны?
Это не многоугольник.
Это луч АВ.
Это не кривая линия.
Это не луч.
Это отрезок.
Ответ:
Это луч AB

13. Собираясь домой, гости надели 4 пальто и 7 плащей, после чего вешалка опустела. Сколько гостей ушли домой?
Ответ:
4 + 7 = 11 вещей — надели гости, т.е. 11 гостей ушли домой

14. На двух полках стояло по 15 книг. С одной полки взяли несколько книг, а с другой взяли столько книг, сколько осталось на первой полке. Сколько всего взяли книг?
Ответ:
Допустим, что с первой полки взяли 6 книг, а со второй полки взяли столько книг, сколько осталось на первой полке.
На первой полке осталось 15 — 6 = 9 книг, значит со второй полки взяли 9 книг.
6 + 9 = 15 книг — взяли всего

Страница 90

15. В магазине продают печенье, шоколад, конфеты, вафли.
У Антона 90 рублей. Может ли он купить:
2 плитки шоколада;
пачку печенья и шоколадку;
пачку вафель, пачку печенья и плитку шоколада;
коробку конфет;
3 пачки печенья;
2 пачки вафель, шоколадку и пачку печенья?
Ответ:
2 плитки шоколада стоят: 38 + 38 = 76 рублей
90 рублей > 76 рублей, значит Антон сможет купить 2 плитки шоколада.
Пачка печенья и шоколадка стоят: 12 + 38 = 50 рублей
90 рублей > 50 рублей, значит Антон сможет купить пачку печенья и шоколадку.
Пачка вафель, пачка печенья и плитка шоколада стоят: 30 + (12 + 38) = 30 + 50 = 80 рублей
90 рублей >> 80 рублей, значит Антон сможет купить пачку вафель, пачку печенья и плитку шоколада.
Коробка конфет стоит 96 рублей
90 рублей 36 рублей, значит Антон сможет купить 3 пачки печенья.
2 пачки вафель, шоколадка и пачка печенья стоят: (30 + 30) + (38 + 12) = 60 + 50 = 110 рублей
90 рублей □ + □ ) + □ = 39.
Ответ:
1) Сначала узнаем сколько пирожков было с мясом и капустой:
12 + 15 = 27 пирожков
2) Затем узнаем сколько пирожков было с рисом:
39 — 27 = 12 пирожков
Проверка решения: (12 + 15) + 12 = 39

21. Выполни действия, записывая числа столбиком.
68 + 24 52 + 9 64 — 17 50 — 16
42 + 58 64 + 7 85 — 58 70 — 43
73 + 16 8 + 92 51 — 44 90 — 8
19 + 27 4 + 49 77 — 69 63 — 4
Ответ:

22. В некоторых числах одна из цифр в записи заменена звёздочкой. В тех случаях, где возможно, сравни пары чисел.
3 ∗ и 51 99 и ∗ 7 7 ∗ и ∗ 8
∗ 5 и ∗ 4 6 ∗ и 8 ∗ 8 ∗ и 9 ∗
Поясни свой ответ.
Ответ:
3 ∗ и 51 — 3 десятка меньше, чем 5 десятков, поэтому какая бы цифра (от 0 до 9) вместо ∗ не стояла, число 3 ∗ всегда будет меньше 51. Так что 3 ∗ ∗ 5 и ∗ 4 — в обоих случаях ∗ стоит на месте разряда десятков, поэтому пары нельзя сравнить
99 и ∗ 7 — 99 самое большое двузначное число, поэтому оно больше любого другого двузначного числа. Так что 99 > ∗ 7
6 ∗ и 8 ∗ — 6 десятков меньше, чем 8 десятков, поэтому какая бы цифра (от 0 до 9) вместо ∗ не стояла, число 6 ∗ всегда будет меньше 8 ∗ . Так что 6 ∗ 8 ∗
7 ∗ и ∗ 8 — в первом числе 7 десятков, во втором числе на месте разряда десятков стоит ∗ , вместо которой может стоять цифра больше 7, равно 7 или меньше 7, поэтому пары нельзя сравнить
8 ∗ и 9 ∗ — 8 десятков меньше, чем 9 десятков, поэтому какая бы цифра (от 0 до 9) вместо ∗ не стояла, число 8 ∗ всегда будет меньше 9 ∗ . Так что 8 ∗ 9 ∗

23. Объясни, как составлены ряды чисел. Назови ещё по три следующих числа.
1, 6, 11, 16 . .
20, 17, 14, 11 .
1, 2, 3, 5, 8 . .
Ответ:
В первом ряду каждое следующее число больше предыдущего на 5: 1, 6, 11, 16, 21, 26, 31
Во второму ряду каждое следующее число меньше предыдущего на 3: 20, 17, 14, 11, 8, 5, 2
В третьем ряду следующее число равно сумме двух предыдущих чисел: 1, 2, 3, 5, 8, 13, 21, 34

Страница 92

24. Уменьши: 80 на 18, 92 на 3, 49 на 17, 50 на 25.
Ответ:

25. Выясни, каков твой рост и рост твоего соседа по парте. Вычисли, на сколько сантиметров один из вас выше другого.
Ответ:
Например: рост первого ученика равен 130 см, а рост второго ученика равен 137 см.
137 — 130 = 7 см — второй ученик выше, чем первый

26. Сравни следующие примеры между собой. Чем они похожи и чем различаются?
100 — 45 100 — 8
100 — 64 100 — 96
Не выполняя вычислений, перепиши эти примеры в порядке увеличения их ответов.
Проверь себя: выполни вычисления.
Ответ:
У всех примеров одинаковое уменьшаемое (число 100).
Чем больше число вычитаем из уменьшаемого, тем меньше будет значение разности.
Поэтому примеры в порядке увеличения их ответов будут выглядеть так: 100 — 96; 100 — 64; 100 — 45; 100 — 8

27. Какое слово надо вставить, чтобы получилось верное утверждение? Выбери.
Канюк — это . .
1) растение 2) лодка 3) птица 4) рыба
Для ответа на вопрос можно воспользоваться толковым словарём русского языка.
Ответ:
Канюк — это хищная птица, обитающая в Старом Свете.

🎥 Видео

Всё про углы в окружности. Геометрия | МатематикаСкачать

№148. На прямой даны две точки А и В. На продолжении луча ВА отложите отрезок ВС так, чтобы ВС= 2АВ.Скачать

Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Окружность. 7 класс.Скачать

Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Внешнее сопряжение двух дуг окружностей третьей дугой. Урок13.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

1 2 4 сопряжение окружностейСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Внутреннее сопряжение двух дуг окружностей третьей дугой. Урок14.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Трапеция | Задачи 1-10 | Решение задач | Волчкевич |Уроки геометрии в задачах 7-8Скачать

7 класс. Построение. Часть 10. Задача 285Скачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Уравнение окружности (1)Скачать

Сопряжение окружностейСкачать

ЗАДАЧИ НА ПОСТРОЕНИЕ. §22 геометрия 7 классСкачать