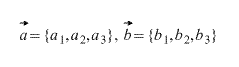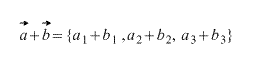Как найти сумму векторов из одной точки

Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow ) .

Существование: Имеем два следующих случая:

Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow ) .

Из данного выше построения сразу же будет следовать единственность данного вектора.

Видео:Сложение векторов. 9 класс.Скачать

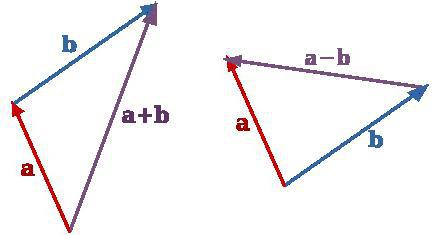
Сумма векторов. Сложение векторов. Правило треугольника

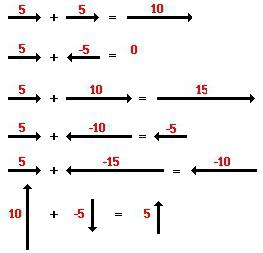
Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.

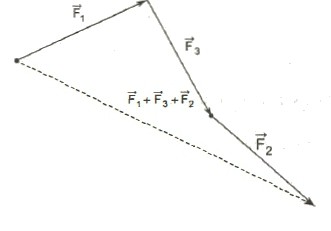
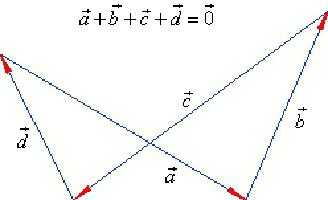
Суммой нескольких векторов ( vec ) , ( vec ) , ( vec,;ldots ) называется вектор ( vec ) , получающийся в результате последовательного сложения данных векторов.

Такая операция выполняется по правилу многоугольника.

Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec + vec = left( <+ , + , + > right) )

Отметим несколько свойств сложения двух векторов:

Для произвольного вектора ( overrightarrow ) выполняется равенство

Для произвольных точек ( A, B и C ) справедливо следующее равенство

Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.

Видео:8 класс, 43 урок, Сумма двух векторовСкачать

Разность векторов. Вычитание векторов

Разность двух одинаковых векторов равна нулевому вектору :
( vec — vec = vec )

Длина нулевого вектора равна нулю:
( left| vec right| = 0 )

Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec — vec = left( <- , — , — > right) )

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Умножение вектора на число

Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .

Определение Произведением вектора ( overrightarrow ) на действительное число ( k ) называется вектор ( overrightarrow ) удовлетворяющий следующим условиям:

Длина вектора ( overrightarrow ) равна ( left|overrightarrowright|=left|kright||overrightarrow| ) ;

Векторы ( overrightarrow ) и ( overrightarrow ) сонаправлены, при ( kge 0 ) и противоположно направлены, если ( kle 0 )

Обозначение: ( overrightarrow=koverrightarrow ) .

Видео:Вычитание векторов. 9 класс.Скачать

Правила, по которым происходит сложение векторов

Как происходит сложение векторов, не всегда понятно ученикам. Дети не представляют того, что за ними скрывается. Приходится просто запоминать правила, а не вдумываться в суть. Поэтому именно о принципах сложения и вычитания векторных величин требуется много знаний.

В результате сложения двух и более векторов всегда получается еще один. Причем он всегда обязательно будет одинаковым, независимо от приема его нахождения.

Чаще всего в школьном курсе геометрии рассматривается сложение двух векторов. Оно может быть выполнено по правилу треугольника или параллелограмма. Эти рисунки выглядят по-разному, но результат от действия один.

Видео:Сложение векторов. Правило параллелограмма. 9 класс.Скачать

Как происходит сложение по правилу треугольника?

Оно применяется тогда, когда векторы неколлинеарные. То есть не лежат на одной прямой или на параллельных.

В этом случае от некоторой произвольной точки нужно отложить первый вектор. Из его конца требуется провести параллельный и равный второму. Результатом станет вектор, исходящий из начала первого и завершающийся в конце второго. Рисунок напоминает треугольник. Отсюда и название правила.

Если векторы коллинеарные, то это правило тоже можно применять. Только рисунок будет расположен вдоль одной линии.

Видео:СУММА ВЕКТОРОВ правило треугольникаСкачать

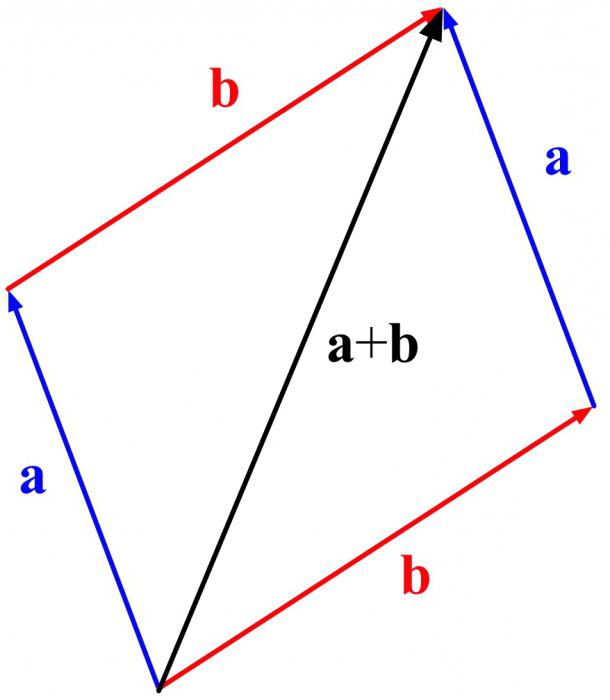
Как выполняется сложение по правилу параллелограмма?

Опять же? применяется только для неколлинеарных векторов. Построение выполняется по другому принципу. Хотя начало такое же. Нужно отложить первый вектор. И от его начала — второй. На их основе достроить параллелограмм и провести диагональ из начала обоих векторов. Она и будет результатом. Так выполняется сложение векторов по правилу параллелограмма.

До сих пор их было два. А как быть, если их 3 или 10? Использовать следующий прием.

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Как и когда применяется правило многоугольника?

Если требуется выполнить сложение векторов, число которых — больше двух, пугаться не стоит. Достаточно последовательно отложить их все и соединить начало цепочки с ее концом. Этот вектор и будет искомой суммой.

Видео:Правило параллелепипеда для векторовСкачать

Какие свойства действительны для действий с векторами?

О нулевом векторе. Которое утверждает, что при сложении с ним получается исходный.

О противоположном векторе. То есть о таком, который имеет противоположное направление и равное по модулю значение. Их сумма будет равна нулю.

О коммутативности сложения. То, что известно еще с начальной школы. Смена мест слагаемых не приводит к изменению результата. Другими словами, неважно какой вектор откладывать сначала. Ответ все равно будет верным и единственным.

Об ассоциативности сложения. Этот закон позволяет складывать попарно любые векторы из тройки и к ним прибавлять третий. Если записать это с помощью знаков, то получится следующее:

первый + (второй + третий) = второй + (первый + третий) = третий + (первый + второй).

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Что известно о разности векторов?

Отдельной операции вычитания не существует. Это связано с тем, что оно, по сути, является сложением. Только второму из них задается противоположное направление. А потом все выполняется так, как если бы рассматривалось сложение векторов. Поэтому об их разности практически не говорят.

Для того чтобы упростить работу с их вычитанием, видоизменено правило треугольника. Теперь (при вычитании) второй вектор нужно отложить из начала первого. Ответом будет тот, что соединяет конечную точку уменьшаемого с ней же вычитаемого. Хотя можно и откладывать так, как было описано ранее, просто изменив направление второго.

Видео:Геометрия 9 класс (Урок№2 - Сумма двух векторов. Законы сложения векторов.)Скачать

Как найти сумму и разность векторов в координатах?

В задаче даны координаты векторов и требуется узнать их значения для итогового. При этом построений выполнять не нужно. То есть можно воспользоваться несложными формулами, которые описывают правило сложения векторов. Они выглядят так:

а (х, у, z) + в (k, l, m) = с (х+k, y+l, z+m);

а (х, у, z) -в (k, l, m) = с (х-k, y-l, z-m).

Легко заметить, что координаты нужно просто сложить или вычесть в зависимости от конкретного задания.

Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Первый пример с решением

Условие. Дан прямоугольник АВСД. Его стороны равны 6 и 8 см. Точка пересечения диагоналей обозначена буквой О. Требуется вычислить разность векторов АО и ВО.

Решение. Сначала нужно изобразить эти векторы. Они направлены от вершин прямоугольника к точке пересечения диагоналей.

Если внимательно посмотреть на чертеж, то можно увидеть, что векторы уже совмещены так, чтобы второй из них соприкасался с концом первого. Вот только его направление неверное. Он должен из этой точки начинаться. Это если векторы складываются, а в задаче — вычитание. Стоп. Это действие означает, что нужно прибавить противоположно направленный вектор. Значит, ВО нужно заменить на ОВ. И получится, что два вектора уже образовали пару сторон из правила треугольника. Поэтому результат от их сложения, то есть искомая разность, — вектор АВ.

А он совпадает со стороной прямоугольника. Для того чтобы записать числовой ответ, потребуется следующее. Начертить прямоугольник вдоль так, чтобы большая сторона шла горизонтально. Нумерацию вершин начинать с левой нижней и идти против часовой стрелки. Тогда длина вектора АВ будет равна 8 см.

Ответ. Разность АО и ВО равна 8 см.

Видео:10 класс, 40 урок, Сложение и вычитание векторовСкачать

Второй пример и его подробное решение

Условие. У ромба АВСД диагонали равны 12 и 16 см. Точка их пересечения обозначена буквой О. Вычислите длину вектора, образованного разностью векторов АО и ВО.

Решение. Пусть обозначение вершин ромба будет таким же, как в предыдущей задаче. Аналогично решению первого примера получается, что искомая разность равна вектору АВ. А его длина неизвестна. Решение задачи свелось к тому, чтобы вычислить одну из сторон ромба.

Для этой цели потребуется рассмотреть треугольник АВО. Он прямоугольный, потому что диагонали ромба пересекаются под углом в 90 градусов. А его катеты равны половинам диагоналей. То есть 6 и 8 см. Искомая в задаче сторона совпадает с гипотенузой в этом треугольнике.

Для ее нахождения потребуется теорема Пифагора. Квадрат гипотенузы будет равен сумме чисел 6 2 и 8 2 . После возведения в квадрат получатся значения: 36 и 64. Их сумма — 100. Отсюда следует, что гипотенуза равна 10 см.

Ответ. Разность векторов АО и ВО составляет 10 см.

Видео:ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

Третий пример с детальным решением

Условие. Вычислить разность и сумму двух векторов. Известны их координаты: у первого — 1 и 2, у второго — 4 и 8.

Решение. Для нахождения суммы потребуется сложить попарно первые и вторые координаты. Результатом будут числа 5 и 10. Ответом будет вектор с координатами (5; 10).

Для разности нужно выполнить вычитание координат. После выполнения этого действия получатся числа -3 и -6. Они и будут координатами искомого вектора.

Ответ. Сумма векторов — (5; 10), их разность — (-3; -6).

Видео:10 класс, 41 урок, Сумма нескольких векторовСкачать

Четвертый пример

Условие. Длина вектора АВ равна 6 см, ВС — 8 см. Второй отложен от конца первого под углом в 90 градусов. Вычислить: а) разность модулей векторов ВА и ВС и модуль разности ВА и ВС; б) сумму этих же модулей и модуль суммы.

Решение: а) Длины векторов уже даны в задаче. Поэтому вычислить их разность не составит труда. 6 — 8 = -2. Несколько сложнее обстоит дело с модулем разности. Сначала нужно узнать, какой вектор будет являться результатом вычитания. Для этой цели следует отложить вектор ВА, который направлен в противоположную сторону АВ. Потом от его конца провести вектор ВС, направив его в сторону, противоположную исходному. Результатом вычитания получится вектор СА. Его модуль можно вычислить по теореме Пифагора. Несложные вычисления приводят к значению 10 см.

б) Сумма модулей векторов получается равной 14 см. Для поиска второго ответа потребуется некоторое преобразование. Вектор ВА противоположно направлен тому, который дан — АВ. Оба вектора направлены из одной точки. В этой ситуации можно использовать правило параллелограмма. Результатом сложения будет диагональ, причем не просто параллелограмма, а прямоугольника. Его диагонали равны, значит, модуль суммы такой же, как в предыдущем пункте.

Видео:Построить разность векторов.Скачать

Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор.

Видео:Сложение и вычитание векторов. Практическая часть. 11 класс.Скачать

Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор

В механике существуют два типа величин:

• скалярные величины, задающие некоторое числовое значение — время, температура, масса и т.д.
• векторные величины, которые вместе с некоторым числовым значением задают направление — скорость, сила и т.д..

Рассмотрим сначала алгебраический подход к сложению векторов.

Покоординатное сложение векторов.

Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:

В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.

Теперь перейдем к геометрическому смыслу сложения двух векторов:

При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:

• правило параллелограмма
• правило треугольника
• тригонометрический способ

Правило параллелограмма. Сложение векторов по правилу параллелограмма.

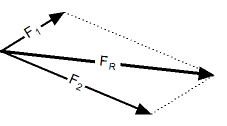Процедура сложения векторов по правилу параллелограмма заключается в следующем: нарисовать первый вектор, учитывая его величину и направление от начала первого вектора нарисовать второй вектор, также используя и его величину, и его направление дополнить рисунок до параллелограмма, считая, что два нарисованных вектора — это его стороны результирующим вектором будет диагональ параллелограмма, причем его начало будет совпадать с началом первого (а, значит, и второго) вектора.

Правило треугольника. Сложение векторов по правилу треугольника.

	Сложение векторов по правилу треугольника заключается в следующем: нарисовать первый вектор, используя данные о его длине ( числовой величине) и направлении от конца первого вектора нарисовать второй вектор, также учитывая и его размер, и его направление результирующим вектором будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом второго.

Тригонометрический способ. Сложение векторов тригонометрическим способом.

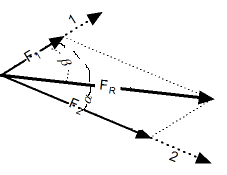Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов: Fрез. = [ F1 2 + F2 2 -2 F1 F2 cos(180 о -α) ] 1/2 (1) где F = числовое значение вектора α = угол между векторами 1 и 2 Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов: β = arcsin[ F2 *sin(180 o -α) / FR ] (2) где α = угол между исходными векторами

Пример — сложение векторов.

Сила 1 равна 5кН и воздействует на тело в направлении, на 80 o отличающемся от направления действия второй силы, равной 8 кН.

Результирующая сила вычисляется следующим образом:

F_рез = [ (5 кН) 2 + (8 кН) 2 — 2 (5 кН)(8 kН) cos(180 o — (80 o )) ] 1/2

Угол между результирующей силой и первой силой равен:

А угол между второй и результирующей силой можно посчитать следующим образом: as

α = arcsin [ (5 кН) sin(180 o — (80 o )) / (10,2 кН) ]

Он-лайн калькулятор сложения векторов.

Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.

Консультации и техническая
поддержка сайта: Zavarka Team

📹 Видео

Сложение, вычитание, умножение на число векторов через координату. 9 класс.Скачать

Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

10 класс, 44 урок, Правило параллелепипедаСкачать

8 класс, 45 урок, Сумма нескольких векторовСкачать