По двум длинным прямолинейным и параллельным проводам, расстояние между которыми d = 4 см, в противоположных направлениях текут токи I1 = 0,3 А, I2 = 0,5 А. Найти магнитную индукцию поля в точке А, которая находится на расстоянии r = 2 см от первого и провода на продолжении линии, соединяющей провода (рис.8).
Решение.
| Рисунок 8 |
На рис. 8 провода расположены перпендикулярно плоскости чертежа. Маленькими кружочками изображены сечения проводив. Условимся, что ток I1, течет к нам, а ток I2   от нас. Общая индукция В в точке А равна векторной (геометрической) сумме индукции В1, и В1 полей, создаваемых каждым током в отдельности т. е,
Для того чтобы найти направление вектора В1 и В2, проведем через точку А силовые линии магнитных полей, созданных токами I1 и I2.
Силовые линии магнитного поля прямого провода с током представляют собой концентрические окружности с центром на оси провода. Направление силовой линии совпадает с движением концов рукоятки правого буравчика, ввинчиваемого во направлению тока (правило буравчика) Поэтому силовая линия магнитного поля тока I1, проходящая через точку А, представляет собой окружность радиусом I1 A, а силовая линии магнитного поля тока I2, проходящая через эту же точку, — окружность радиусом I2 A (на рис. 8 показана только часто этой окружности). По правилу буравчика находим, что силовая линия магнитного ноля тока I1 направлена против часовой стрелки, а тока I2 по часовой стрелке.
Теперь легко найти направления векторов В1 и В2 в точке А: каждый из них направлен по касательной к соответствующей силовой линии в этой точке. Так как векторы В1 и В2 направлены вдоль одной прямой в противоположные стороны, то векторное равенство (1) можно заменить алгебраическим равенством
Индукция магнитного поля тока I, текущего по прямому бесконечно длинному проводу, вычисляется по формуле
где μ0   магнитная постоянная; μ   магнитная пропицаемость среды, в которой провод расположен; r  расстояние от провода до точки, в которой определяется индукция. Подставив выражения В1 и В2 в равенство (2), получим
Запишем в СИ числовые значения некоторых величии: r1 = 0,02 м, r2 = d+r1 = 0,06 м, μ0 = 4π ·10 -7 Гн/м, μ = 1. Вычислим искомую индукцию:
- Пример 2.
- Пример 3.
- Пример 4.
- Пример 5.
- Пример 6.
- Пример 7.
- Пример 8.
- Магнитное поле и его характеристики
- теория по физике 🧲 магнетизм
- Основные свойства магнитного поля
- Вектор магнитной индукции
- Напряженность магнитного поля
- Направление вектора магнитной индукции и способы его определения
- Магнитное поле прямолинейного тока
- Магнитное поле кругового тока
- Магнитное поле электромагнита (соленоида)
- Алгоритм определения полярности электромагнита
- Магнитная индукция, магнитный поток: определение, формулы, смысл
- Физический смысл магнитной индукции
- Формула магнитной индукции
- Формула магнитной индукции:
- Другие формулы, где встречается B
- Сила Ампера:
- Сила Лоренца:
- Магнитный поток:
- Магнитный поток
- Взаимодействие магнитов
- Направление вектора МИ
- Наглядное отображение линий МИ
- Основные формулы для вычисления вектора МИ
- Закон электромагнитной индукции
- Закон Био-Савара-Лапласа
- Принцип суперпозиции
- Правило Ленца
- Электромагнитная индукция
- 💡 Видео
Пример 2.
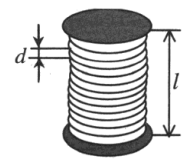
Из проволоки диаметром d = 0,01 мм и сопротивлением r = 25 Ом намотан соленоид на картонном цилиндре (витки вплотную прилегают друг к другу). Определить индукцию магнитного поля на оси соленоида, если напряжение на концах обмотки U = 2 В.
Индукция магнитного поля на оси соленоида вычисляется по формуле
Здесь n = 1/d; d диаметр проволоки; n число витков на единицу длины соленоида; I сила тока, текущего по обмотке соленоида. Силу тока, текущего по обмотке, найдём по закону Ома для участка цепи:
Подставим значения n и I в равенство (1):
Выпишем числовые значения величин входящих в (2), в СИ: μ0 = 4π ·10 -7 Гн/м, μ = 1. d = 10 -4 м. Вычисления:
Пример 3.
Прямой провод длиной l = 10 см, по которому течет ток I = 0,5 А, помещен в однородное магнитное поле перпендикулярно силовым линиям. Найти индукцию магнитного поля, если оно действует на прямой провод с силой F = 2,6 мН.
Сила, с которой однородное магнитное поле действует на прямой провод с током, вычисляется по закону Ампера:
где I сила тока, текущего по проводнику; l длина проводника; В индукция магнитного поля, в которое проводник помещён; а- угол между направлениями тока и линий индукции. Из формулы (1) найдем
Выпишем числовые значения величин входящих в (2), в СИ: F = 2,6· 10 -3 Н; I = 0,5 А; l = 0,1 м; α = 90º; sinα = 1. Вычисления:
Пример 4.
Протон, пройдя ускоряющую разность потенциалов U = 400 В, влетел в однородное магнитное поле с индукцией В = 0,2 Тл и начал двигаться по окружности. Вычислить радиус окружности.
На заряженную частицу, влетевшую в магнитное поле, действует сила Fл, называемая силой Лоренца. Она вычисляется по формуле , где e заряд частицы; v ее скорость; В индукция магнитного поля, в котором движется частица; α угол между направлениями векторов скорости и индукции. Поскольку по условию задачи протон движется по замкнутой траектории (окружности), можно заключить, что составляющая вектора скорости в направлении вектора В равна нулю, т. е. α = 90º, sinα = 1.
Направление силы Лоренца подчиняется, как известно, правилу левой руки. Угол между направлениями v и Fл всегда составляет 90º. Следовательно, сила Лоренца является центростремительной силой, т.е. или
где m масса протона; R радиус окружности, по которой движется протон. Тогда
Протон получил скорость, пройдя, ускоряющую разность потенциалов По закону сохранения энергии работа, совершенная полем при перемещении протона, равна кинетической энергии, приобретенной протоном, т, е.
Работа сил электрического поля при перемещении протона определяется по формуле
Кинетическая энергия протона
Подставив выражение А по (З) и выражение Т по (4) в (2), получим , откуда
Подставляя выражение для v в (1), находим
Проверим расчетную формулу (6):
Выпишем в СИ числовые значения недостающих величин ; . Вычислим искомый радиус
Пример 5.
Ток, текущий в рамке, содержащей N витков, создаст магнитное поле. В центре рамки индукция поля B = 0,126 Тл. магнитный момент рамки, если ее радиус R = 10 см.
Магнитный момент рамки с током
где I — сила тока в витке; площадь, охватываемая витком N — число витков рамке. Индукция магнитного поля в центре кругового тока (многовиткового) , откуда Подставляя в (1) выражения для I и S, получаем
Выпишем числовые значения величин, входящих в (2), в СИ: Вычислим искомый магнитный момент:
Пример 6.
Плоская рамка площадью содержащая S = 100 см 2 , содержащая N = 20 витков тонкого провода, вращается в однородном магнитном поле с индукцией В = 100 мТл. Амплитуда э.д.с. индукции εмакс = 10 В. Определить частоту вращения рамки.
Используя понятие угловой скорости вращении (ω = 2π/T = 2πn, где T период вращения; n частота вращения), определим частоту вращения рамки:
Угловую скорость вращения найдем из соотношения
Где ε мгновенное значение э.д.с. индукции. Амплитудой ε является значение εмакс , соответствующее значению sinωt = 1. Из соотношения (2) имеем
Подставив выражение ω по (3) в (1),получаем
Выразим значения ряда величин, входящих в формулу (4), в СИ: Выполним вычисления:
Пример 7.
На немагнитный каркас длиной l = 50 см и площадью сечения S = 3см 2 намотан в одни слой провод диаметром d = 0,4 мм так, что витки плотно прилегают друг к другу. Найти: 1) индуктивность получившегося соленоида и 2) магнитный поток, пронизывающий поперечное сечение соленоида при токе силой I = 1 А.
Индуктивность соленоида вычисляется по формуле
где n число витков, приходящихся на единицу длины соленоида; V объем соленоида. Число витков n получим, разделив единицу длины на диаметр провода:
Объем соленоида V = Sl, где S площадь поперечного сечения соленоида; l длина соленоида. Подставим выражения для n и V в равенство (1):
Выпишем числовые значения величин, входящих в (3), в СИ:
При наличии тока в соленоиде любое его поперечное сечение пронизывает магнитный поток
где В магнитная индукция в соленонде. Магнитная индукция соленоида определяется по формуле
| B = μ0μIn. | (5) |
Подставив выражения n и В по (2) и (5) в (4), получим расчетную формулу
Выполним вычисления, подставив в расчетную формулу значения величин I, S и d в СИ:
Пример 8.
Колебательный контур состоит из плоского воздушного конденсатора с двумя пластинами площадью по S = 100 см ² каждая и катушки с индуктивностью L = 10 -5 Гн. Период колебаний в контуре Т = 10 -7 с. Определить расстояние между пластинами конденсатора.
Из формулы емкости плоского конденсатора
(ε0 электрическая постоянная; ε диэлектрическая проницаемость среды мёжду пластинами конденсатора; S площадь пластины конденсатора; d расстояние между пластинами) может быть найдено искомое расстояние
Из формулы Томсона, определяющей период колебаний Т в колебательном контуре, найдем емкость ), где L индуктивность катушки. Подставив это выражение С в (1), получим
Выразим некоторые величины, входящие в расчетную формулу (4), в СИ:
Видео:Индукция магнитного поля | Физика 9 класс #37 | ИнфоурокСкачать

Магнитное поле и его характеристики
теория по физике 🧲 магнетизм
Магнитное поле — особая форма материи, посредством которой осуществляется взаимодействие между движущимися электрическими частицами.
Основные свойства магнитного поля
- Магнитное поле порождается электрическим током (движущимися зарядами).
- Магнитное поле обнаруживается по действию на электрический ток (движущиеся заряды).
- Магнитное поле существует независимо от нас, от наших знаний о нем.
Видео:Урок 276. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

Вектор магнитной индукции
Вектор магнитной индукции — силовая характеристика магнитного поля. Она определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью. Обозначается как → B . Единица измерения — Тесла (Тл).
За единицу магнитной индукции можно принять магнитную индукцию однородного поля, котором на участок проводника длиной 1 м при силе тока в нем 1 А действует со стороны поля максимальная сила, равна 1 Н. 1 Н/(А∙м) = 1 Тл.
Модуль вектора магнитной индукции — физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины проводника:
B = F A m a x I l . .
За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле.
Наглядную картину магнитного поля можно получить, если построить так называемые линии магнитной индукции. Линиями магнитной индукции называют линии, касательные к которым направлены так же, как и вектор магнитной индукции в данной точке поля.
Особенность линий магнитной индукции состоит в том, что они не имеют ни начала, ни конца. Они всегда замкнуты. Поля с замкнутыми силовыми линиями называют вихревыми. Поэтому магнитное поле — вихревое поле.
Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобным электрическим, в природе нет.
Видео:Радиус описанной окружностиСкачать

Напряженность магнитного поля
Вектор напряженности магнитного поля — характеристика магнитного поля, определяющая густоту силовых линий (линий магнитной индукции). Обозначается как → H . Единица измерения — А/м.
μ — магнитная проницаемость среды (у воздуха она равна 1), μ 0 — магнитная постоянная, равная 4 π · 10 − 7 Гн/м.
Внимание! Направление напряженности всегда совпадает с направлением вектора магнитной индукции: → H ↑↑ → B .
Видео:Радиус и диаметрСкачать

Направление вектора магнитной индукции и способы его определения
Чтобы определить направление вектора магнитной индукции, нужно:
- Расположить в магнитном поле компас.
- Дождаться, когда магнитная стрелка займет устойчивое положение.
- Принять за направление вектора магнитной индукции направление стрелки компаса «север».
В пространстве между полюсами постоянного магнита вектор магнитной индукции выходит из северного полюса:
При определении направления вектора магнитной индукции с помощью витка с током следует применять правило буравчика:
При вкручивании острия буравчика вдоль направления тока рукоятка будет вращаться по направлению вектора → B магнитной индукции.
Отсюда следует, что:
- Если по витку ток идет против часовой стрелки, то вектор магнитной индукции → B направлен вверх.
- Если по витку ток идет по часовой стрелке, то вектор магнитной индукции → B направлен вниз.
Способы обозначения направлений векторов:
| Вверх |  |
| Вниз |  |
| Влево |  |
| Вправо |  |
| На нас перпендикулярно плоскости чертежа |  |
| От нас перпендикулярно плоскости чертежа |  |
Пример №1. На рисунке изображен проводник, по которому течет электрический ток. Направление тока указано стрелкой. Как направлен (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) вектор магнитной индукции в точке С?
Если мысленно начать вкручивать острие буравчика по направлению тока, то окажется, что вектор магнитной индукции в точке С будет направлен к нам — к наблюдателю.
Видео:Урок 281. Электромагнитная индукция. Магнитный поток. Правило ЛенцаСкачать

Магнитное поле прямолинейного тока
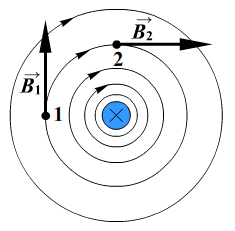
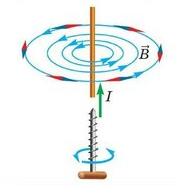
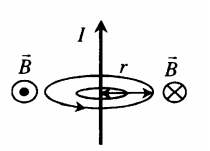
Линии магнитной индукции представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной проводнику. Центр окружностей совпадает с осью проводника.
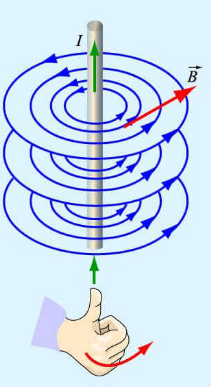
Если ток идет вверх, то силовые линии направлены против часовой стрелки. Если вниз, то они направлены по часовой стрелке. Их направление можно определить с помощью правила буравчика или правила правой руки:
Правило буравчика (правой руки)
Если большой палец правой руки, отклоненный на 90 градусов, направить в сторону тока в проводнике, то остальные 4 пальца покажут направление линий магнитной индукции.
Модуль вектора магнитной индукции на расстоянии r от оси проводника:
B = μ μ 0 I 2 π r . .
Магнитное поле кругового тока
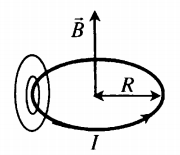
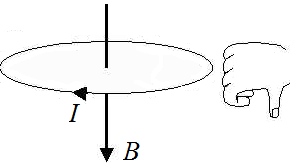
Силовые линии представляют собой окружности, опоясывающие круговой ток. Вектор магнитной индукции в центре витка направлен вверх, если ток идет против часовой стрелки, и вниз, если по часовой стрелке.
Определить направление силовых линий магнитного поля витка с током можно также с помощью правила правой руки:
Если расположить четыре пальца правой руки по направлению тока в витке, то отклоненный на 90 градусов большой палец, покажет направление вектора магнитной индукции.
Модуль вектора магнитной индукции в центре витка, радиус которого равен R:
Модуль напряженности в центре витка:
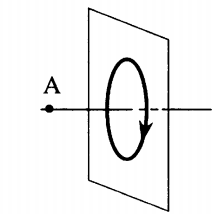
Пример №2. На рисунке изображен проволочный виток, по которому течет электрический ток в направлении, указанном стрелкой. Виток расположен в вертикальной плоскости. Точка А находится на горизонтальной прямой, проходящей через центр витка. Как направлен (вверх, вниз, влево, вправо) вектор магнитной индукции магнитного поля в точке А?
Если мысленно обхватить виток так, чтобы четыре пальца правой руки были бы направлены в сторону тока, то отклоненный на 90 градусов большой палец правой руки показал бы, что вектор магнитной индукции в точке А направлен вправо.
Видео:Правило рук 👋 КАК ЛЕГКО определять НАПРАВЛЕНИЕ ЛИНИЙ МАГНИТНОГО ПОЛЯ??Скачать

Магнитное поле электромагнита (соленоида)
Соленоид — это катушка цилиндрической формы, витки которой намотаны вплотную, а длина значительно больше диаметра.
Число витков в соленоиде N определяется формулой:
l — длина соленоида, d — диаметр проволоки.
Линии магнитной индукции являются замкнутыми, причем внутри соленоида они располагаются параллельно друг другу. Поле внутри соленоида однородно.
Если ток по виткам соленоида идет против часовой стрелки, то вектор магнитной индукции → B внутри соленоида направлен вверх, если по часовой стрелке, то вниз. Для определения направления линий магнитной индукции можно воспользоваться правилом правой руки для витка с током.
Модуль вектора магнитной индукции в центральной области соленоида:
B = μ μ 0 I N l . . = μ μ 0 I d . .
Модуль напряженности магнитного поля в центральной части соленоида:
H = I N l . . = I d . .
Алгоритм определения полярности электромагнита
- Определить полярность источника.
- Указать на витках электромагнита условное направление тока (от «+» источника к «–»).
- Определить направление вектора магнитной индукции.
- Определить полюса электромагнита. Там, откуда выходят линии магнитной индукции, располагается северный полюс электромагнита (N, или «–». С противоположной стороны — южный (S, или «+»).
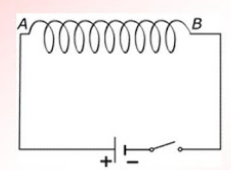
Пример №3. Через соленоид пропускают ток. Определите полюсы катушки.
Ток условно течет от положительного полюса источника тока к отрицательному. Следовательно, ток течет по виткам от точки А к точке В. Мысленно обхватив соленоид пальцами правой руки так, чтобы четыре пальца совпадали с направлением тока в витках соленоида, отставим большой палец на угол 90 градусов. Он покажет направление линий магнитной индукции внутри соленоида. Проделав это, увидим, что линии магнитной индукции направлены вправо. Следовательно, они выходят из В, который будет являться северным полюсом. Тогда А будет являться южным полюсом.
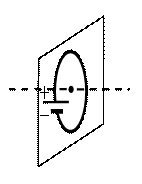
а) вертикально вверх в плоскости витка
б) вертикально вниз в плоскости витка
в) вправо перпендикулярно плоскости витка
г) влево перпендикулярно плоскости витка
Алгоритм решения
Решение
По условию задачи мы имеем дело с круглым проволочным витком. Поэтому для определения вектора → B магнитной индукции мы будем использовать правило правой руки.
Чтобы применить это правило, нам нужно знать направление течение тока в проводнике. Условно ток течет от положительного полюса источника к отрицательному. Следовательно, на рисунке ток течет по витку в направлении хода часовой стрелки.
Теперь можем применить правило правой руки. Для этого мысленно направим четыре пальца правой руки в направлении тока в проволочном витке. Теперь отставим на 90 градусов большой палец. Он показывает относительно рисунка влево. Это и есть направление вектора магнитной индукции.
pазбирался: Алиса Никитина | обсудить разбор | оценить
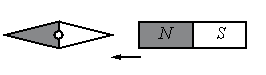
а) повернётся на 180°
б) повернётся на 90° по часовой стрелке
в) повернётся на 90° против часовой стрелки
г) останется в прежнем положении
Алгоритм решения
- Вспомнить, как взаимодействуют магниты.
- Определить исходное положение полюсов.
- Определить конечное положение полюсов и установить, как изменится положение магнитной стрелки.
Решение
Одноименные полюсы магнитов отталкиваются, а разноименные притягиваются. Изначально южный полюс магнитной стрелки находится справа, а северный — слева. Полосовой магнит подносят к ее южному полюсу северной стороной. Поскольку это разноименные полюса, положение магнитной стрелки не изменится.
pазбирался: Алиса Никитина | обсудить разбор | оценить
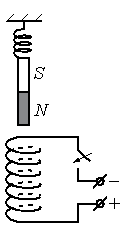
Алгоритм решения
- Определить направление тока в соленоиде.
- Определить полюса соленоида.
- Установить, как будет взаимодействовать соленоид с магнитом.
- Установить, как будет себя вести магнит после замыкания электрической цепи.
Решение
Чтобы определить направление тока в соленоиде, посмотрим на расположение полюсов источника тока. Ток условно направлен от положительного полюса к отрицательному. Следовательно, относительно рисунка ток в витках соленоида направлен по часовой стрелке.
Зная направление тока в соленоиде, можно определить его полюса. Северным будет тот полюс, из которого выходят линии магнитной индукции. Определить их направление поможет правило правой руки для соленоида. Мысленно обхватим соленоид так, чтобы направление четырех пальцев правой руки совпадало с направлением тока в витках соленоида. Теперь отставленный на 90 градусов большой палец покажет направление вектора магнитной индукции. Проделав все манипуляции, получим, что вектор магнитной индукции направлен вниз. Следовательно, внизу соленоида расположен северный полюс, а вверху — южный.
Известно, что одноименные полюса магнитов отталкиваются, а разноименные — притягиваются. Подвешенный полосовой магнит обращен к южному полюсу соленоида северным полюсом. А это значит, что при замыкании электрической цепи он будет растягивать пружину, притягиваясь к соленоиду (двигаться вниз).
pазбирался: Алиса Никитина | обсудить разбор | оценить
Видео:Урок 20. Магнитная индукция, магнитный поток, магнитная цепьСкачать

Магнитная индукция, магнитный поток: определение, формулы, смысл
Видео:ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ сила Ампера правило левой рукиСкачать

Физический смысл магнитной индукции
Физически это явление объясняется следующим образом. Металл имеет кристаллическую структуру (катушка металлическая). В кристаллической решетке металла есть электрические заряды – электроны. Если на металл не действует магнитное воздействие, заряды (электроны) покоятся и никуда не движутся.

Васильев Дмитрий ПетровичПрофессор электротехники Санкт-Петербургского государственного политехнического университета Если металл попадает под действие переменного магнитного поля (из-за движения постоянного магнита внутри катушки – точное смещение), то заряды начинают двигаться под действием влияние этого магнитного поля.
В результате в металле образуется электрический ток. Сила этого тока зависит от физических свойств магнита и катушки и скорости движения одного относительно другого.
Когда металлическую катушку помещают в магнитное поле, заряженные частицы металлической решетки (в каштане) поворачиваются на определенный угол и размещаются вдоль силовых линий магнитного поля.
Чем больше напряженность магнитного поля, тем большее количество частиц вращается и тем более равномерным будет их расположение.
Магнитные поля, ориентированные в одном направлении, не нейтрализуют друг друга, а складываются в единое поле.
Видео:Найти центр и радиус окружностиСкачать

Формула магнитной индукции
где V – вектор магнитной индукции, F – максимальная сила, действующая на проводник с током, I – ток в проводнике, l – длина проводника.
Формула магнитной индукции:

Формула магнитной индукции: B = Mmax / IS
- B – индукция магнитного поля (в Тл)
- Mmax – максимальный крутящий момент магнитных сил, приложенных к раме (в Нм)
- l – длина жилы (в м)
- S – площадь рамы (в м2²)
Другие формулы, где встречается B
Эти формулы также можно использовать для его расчета.
Сила Ампера:

Сила ампер: Fa = IBL sinα
- Fa – сила ампер (в N – ньютон)
- I – сила тока (в А – амперах)
- B – индукция магнитного поля (в Тл)
- L – длина жилы (в м)
- α – угол между вектором B и одним из направлений (текущая сила, скорость и т д.; измеряется в рад или градусах.)
Сила Лоренца:

Сила Лоренца: Fl = qvB sinα
- Fl – сила Лоренца (в Н – Ньютон)
- q – заряд частицы (в Кл – кулонах)
- v – скорость (в м / с)
- B – индукция (в Тл)
- α – угол между вектором B и одним из направлений (текущая сила, скорость или другое; измеряется в рад или градусах.))
Магнитный поток:

Магнитный поток: Ф = BS cosα
- F – магнитный поток (в Вб – вебер)
- B – индукция (в Тл)
- S – площадь рамы (в м2²)
- α – угол между вектором B и одним из направлений (текущая сила, скорость или другое; измеряется в рад или градусах.))
Видео:Физика 9 класс (Урок№19 - Индукция магнитного поля.)Скачать

Магнитный поток
Магнитный поток – это скалярная величина, которая характеризует влияние магнитной индукции на данный металлический контур.
Магнитная индукция определяется количеством силовых линий, пересекающих 1 см2 металлического сечения.
Магнитометры, используемые для его измерения, называются теслометрами.

Абрамян Евгений Павлович Доцент кафедры электротехники Санкт-Петербургского государственного политехнического университета Единицей измерения магнитной индукции в системе СИ является Тесла (Тл).
После прекращения движения электронов в катушке сердечник, если он сделан из мягкого железа, теряет свои магнитные свойства. Если он изготовлен из стали, он может некоторое время сохранять свои магнитные свойства.
Взаимодействие магнитов
Постоянный магнит (или магнитная стрелка) ориентирован по магнитному меридиану Земли. Конец, указывающий на север, называется северным полюсом (N), а противоположный конец – южным полюсом (S). Поднося два магнита ближе, мы замечаем, что одноименные полюса отталкиваются друг от друга, а противоположные – притягиваются (рис. 1).
Если мы разделим полюса, разрезав постоянный магнит на две части, мы обнаружим, что каждая из них также будет иметь по два полюса, то есть это будет постоянный магнит (рис. 2). Оба полюса – север и юг – неотделимы друг от друга, равны.
Магнитное поле, создаваемое Землей или постоянными магнитами, представлено, как электрическое поле, магнитными силовыми линиями. Изображение силовых линий магнитного поля магнита можно получить, положив поверх него лист бумаги, на который ровным слоем насыпают железные опилки. Попадая в магнитное поле, опилки намагничиваются: у каждого из них есть северный и южный полюс. Противоположные полюса имеют тенденцию сближаться, но этому препятствует трение опилок о бумагу. Если вы коснетесь бумаги пальцем, трение уменьшится, и опилки будут притягиваться друг к другу, образуя цепочки, которые представляют собой силовые линии магнитного поля.
На рис. 3 показано положение в поле прямого магнита из опилок и маленькие магнитные стрелки, указывающие направление силовых линий магнитного поля. Это направление принимается за направление северного полюса магнитной стрелки.
Видео:Физика - Магнитное полеСкачать

Направление вектора МИ
Направление магнитных полей может быть указано магнитной стрелкой, помещенной в эти поля. Он будет крутиться до упора. Северный конец стрелки покажет, куда ориентировано B → орт того или иного поля.
Линии магнитной индукции
Точно так же ведет себя кадр с текущим, имея возможность перемещаться в МП без помех. Направленность вектора индукции указывает на ориентацию нормали к такой замкнутой электромагнитной цепи.
Внимание! Здесь используется правило буравчика (правый винт). Если винт вращается так же, как ток направлен в рамку, то поступательное продвижение винта совпадает с направлением положительной нормали.
В некоторых случаях для поиска направления применяется правило правой руки.
Наглядное отображение линий МИ
Линия, к которой можно провести касательную, совпадающую с точкой B →, называется линией магнитной индукции (МИ). С помощью таких линий можно визуально визуализировать магнитное поле. Это замкнутые контуры, перекрывающие токи. Их плотность всегда пропорциональна значению B → в определенной точке МП.
Информация. Что касается МП прямого движения заряженных частиц, то эти линии представлены в виде концентрических окружностей. Их центр расположен на прямой линии с течением и в плоскостях, расположенных под прямым углом к нему.
Направление магнитных линий также можно определить с помощью правила подвеса.
Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Основные формулы для вычисления вектора МИ
Вектор магнитной индукции, формула которого B = Fm / I * ∆L, может быть найден с помощью других математических расчетов.
Закон электромагнитной индукции
Закон электромагнитной индукции (закон Фарадея) звучит так:
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока на поверхности, ограниченной кольцом.
Математически это можно описать формулой:
| Закон Фарадея Ɛi – индукционная ЭДС В ΔФ / Δt – скорость изменения магнитного потока Вт / с |
Знак «-» в формуле позволяет учитывать направление индукционного тока. Индукционный ток в замкнутой цепи всегда направлен так, что магнитный поток поля, создаваемого этим током через поверхность, ограниченную кольцом, уменьшает те изменения поля, которые вызывают появление индукционного тока.
Если цепь состоит из N витков (т.е это катушка), ЭДС индукции будет рассчитываться следующим образом.
| Закон Фарадея для цепи из N витков Ɛi – индукционная ЭДС В ΔФ / Δt – скорость изменения магнитного потока Вт / с N – количество оборотов – |
Сила индукционного тока в замкнутом токопроводящем контуре с сопротивлением R:
| Закон Ома для проводящей цепи Ɛi – индукционная ЭДС В I – сила индукционного тока [А] R – сопротивление цепи [Ом] |
Если проводник длины l будет двигаться со скоростью v в постоянном однородном магнитном поле с индукцией B, ЭДС электромагнитной индукции будет равна:
| Индукционная ЭДС для движущегося проводника Ɛi – индукционная ЭДС В B – магнитная индукция [Тл] v – скорость проводника [м / с] l – длина жилы [м] |
Возникновение индукционного электромагнитного поля в проводнике, движущемся в магнитном поле, объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. В этом случае сила Лоренца играет роль внешней силы.
Проводник, движущийся в магнитном поле, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество тепла в цепи выделяется как за счет работы внешней силы, которая сохраняет скорость проводника неизменной, так и за счет уменьшения кинетической энергии проводника.
Изменение магнитного потока, попадающего в замкнутый контур, может происходить по двум причинам:
- из-за движения цепи или ее частей в постоянном магнитном поле с течением времени. Это тот случай, когда проводники, а вместе с ними и носители свободного заряда движутся в магнитном поле
- из-за изменения во времени магнитного поля с неподвижным контуром. В этом случае возникновение индукционной ЭДС уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея
Следовательно, явления индукции в подвижных и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока в этих двух случаях оказывается различной:
- в случае движущихся проводников ЭДС индукции возникает из-за силы Лоренца
- в случае неподвижных проводников ЭДС индукции является следствием действия вихревого электрического поля на свободные заряды, возникающего при изменении магнитного поля.
Закон Био-Савара-Лапласа
Формула индукции ЭДС
Описывает правила поиска B → магнитного поля, которое создает постоянный электрический ток. Это экспериментально установленная модель. Био и Савар в 1820 году показали это на практике, Лаплас смог его сформулировать. Этот закон является фундаментальным в магнитостатике. На практике рассматривался фиксированный провод малого сечения, по которому пропускался электрический ток. Для исследования был выбран небольшой участок проволоки, который характеризовался вектором dl. Его модуль соответствовал длине рассматриваемого участка, а направление совпадало с направлением тока.
Интересно. Лаплас Пьер Симон предложил также рассматривать движение электрона как ток и на этом утверждении с помощью этого закона доказал возможность определения МП наступающего точечного заряда.
Согласно этому физическому правилу каждый сегмент dl проводника, по которому протекает электрический ток I, образует магнитное поле dB в пространстве вокруг себя с интервалом r и под углом α:
дБ = µ0 * I * dl * sin α / 4 * π * r2,
где это находится:
- дБ – магнитная индукция, Тл;
- µ0 = 4 π * 10-7 – магнитная постоянная, Гн / м;
- I – сила тока, А;
- dl – отрезок жилы, м;
- r – расстояние от точки, где находится магнитная индукция, м;
- α – угол, образованный r и вектором dl.
Важно! Согласно закону Био-Савара-Лапласа, суммируя векторы магнитных полей отдельных секторов, можно определить МП требуемого тока. Он будет равен векторной сумме.
Существуют формулы, описывающие этот закон для отдельных случаев МП:
- поля прямого движения электронов;
- поля кругового движения заряженных частиц.
Формула депутата первого рода:
В = µ * µ0 * 2 * I / 4 * π * r.
Для кругового движения это выглядит так:
В = µ * µ0 * I / 4 * π * r.
В этих формулах µ – (относительная) магнитная проницаемость среды).
Рассматриваемый закон следует из уравнений Максвелла. Максвелл вывел два уравнения для МП, случай, когда электрическое поле постоянно, только что рассматривали Био и Савар.
Принцип суперпозиции
Для МП существует принцип, согласно которому полный вектор магнитной индукции в определенной точке равен векторной сумме всех векторов MI, созданных разными токами в данной точке:
B → = B1 → + B2 → + B3 →… + Bn→
Правило Ленца
Для определения направления индукционного тока необходимо использовать правило Ленца.
С академической точки зрения это правило звучит так: индукционный ток, возбуждаемый в замкнутой цепи при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле предотвращает изменение магнитного потока, вызывая индукционный ток.
Попробуем немного попроще: катушка в данном случае – недовольная бабушка. Они забирают магнитный поток: она несчастна и создает магнитное поле, которое этот магнитный поток хочет восстановить.
Они дают ей магнитный поток, они принимают его, они говорят, они используют его, и она такая – “Потому что ваш магнитный поток сдался мне!” и создает магнитное поле, которое вытесняет этот магнитный поток.
Видео:МАГНИТНОЕ ПОЛЕ за 24 минуты. ЕГЭ Физика. Николай Ньютон. ТехноскулСкачать

Электромагнитная индукция
Электромагнитная индукция – явление возникновения тока в замкнутой проводящей цепи при изменении пронизывающего ее магнитного потока.
Явление электромагнитной индукции было открыто М. Фарадеем.
Майкл Фарадей провел серию экспериментов, которые помогли раскрыть явление электромагнитной индукции.
Время опыта. Две катушки были намотаны на токонепроводящей основе: витки первой катушки располагались между витками второй. Витки одной катушки были замкнуты на гальванометр, а другая была подключена к источнику тока.
Когда ключ был закрыт и ток прошел через вторую катушку, в первой появился импульс тока. Когда ключ был открыт, также наблюдался импульс тока, но ток через гальванометр протекал в обратном направлении.
Опыт два. Первая катушка была подключена к источнику тока, а вторая – к гальванометру. В этом случае вторая катушка переместилась относительно первой. При приближении или удалении катушки регистрировался ток.
Опыт три. Катушка закрывается к гальванометру, и магнит приближается (расширяется) относительно катушки
Вот что показали эти эксперименты:
- Индукционный ток возникает только при изменении линий магнитной индукции.
- Направление тока будет разным при увеличении количества линий и при их уменьшении.
- Сила индукционного тока зависит от скорости изменения магнитного потока. Само поле может меняться или граница может двигаться в неоднородном магнитном поле.
| Почему возникает индукционный ток? Ток в цепи может существовать, когда на свободные заряды действуют внешние силы. Работа этих сил по перемещению одиночного положительного заряда по замкнутой цепи равна ЭДС. 💡 ВидеоДвижение заряженной частицы в магнитном поле | Физика ЕГЭ с Никитой АрхиповымСкачать  Магнитное поле. Магнитная индукция | Физика 11 класс #1 | ИнфоурокСкачать  Физика Протон движется в однородном магнитном поле с магнитной индукцией 20 мТл по окружностиСкачать  Электромагнитная индукция за 1 минутуСкачать  Билет №16 "Теорема о циркуляции и теорема Гаусса для магнитного поля"Скачать  Как магнитное поле назвали магнитной индукциейСкачать  МАГНИТНАЯ ИНДУКЦИЯ 11 класс физика сила Ампера сила ЛоренцаСкачать  |