Как найти радиус вписанной окружности по диагонали квадрата

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в квадрат. Также разберем примеры решения задач для закрепления теоретического материала.

Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Формулы вычисления радиуса вписанной окружности

Через сторону квадрата

Радиус r вписанной в квадрат окружности равняется половине длины его стороны a.

Через диагональ квадрата

Радиус r вписанной в квадрат окружности равняется длине его диагонали d, деленной на произведение числа 2 и квадратного корня из двух.

Видео:Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.Скачать

Примеры задач

Задание 1

Найдите радиус вписанной в квадрат окружности, если известно, что длина его стороны равняется 7 см.

Воспользуемся первой формулой, подставив в него известное значение:

Задание 2

Известно, что радиус вписанной в квадрат окружности составляет 12 см. Найдите длину его диагонали.

Формулу для нахождения диагонали можно вывести из формулы для расчета радиуса круга:

Видео:16 задание ОГЭ 2023 Окружность Квадрат#ShortsСкачать

Найти радиус вписанной окружности квадрата c известной диагональю онлайн с формулами расчётов

Введите в поле «диагональ» Ваше измерение и нажмите «Рассчитать»

Введите данные:

Достаточно ввести только одно значение, остальное калькулятор посчитает сам.

Округление:

Диагональ, диаметр описанной окружности (M) = 10

Радиус вписанной окружности (R1) = (frac) = (frac) = 3.54

Радиус описанной окружности (R2) = (frac) = (frac) = 5

Периметр (P) = (L*4) = (7.07*4) = 28.28

Видео:Формулы для радиуса окружности #shortsСкачать

Как находить радиус окружности вписанной в квадрат

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Нахождение радиуса вписанной в квадрат окружности

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в квадрат. Также разберем примеры решения задач для закрепления теоретического материала.

Видео:Как найти центр и радиус нарисованной окружности #математика #егэ2023 #школа #fyp #shortsСкачать

Формулы вычисления радиуса вписанной окружности

Через сторону квадрата

Радиус r вписанной в квадрат окружности равняется половине длины его стороны a.

Через диагональ квадрата

Радиус r вписанной в квадрат окружности равняется длине его диагонали d, деленной на произведение числа 2 и квадратного корня из двух.

Видео:18 задание из ОГЭ. Найти диагональ квадратаСкачать

Примеры задач

Задание 1

Найдите радиус вписанной в квадрат окружности, если известно, что длина его стороны равняется 7 см.

Воспользуемся первой формулой, подставив в него известное значение:

Задание 2

Известно, что радиус вписанной в квадрат окружности составляет 12 см. Найдите длину его диагонали.

Формулу для нахождения диагонали можно вывести из формулы для расчета радиуса круга:

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Квадрат. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):

Можно дать и другие определение квадрата.

Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.

Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).

Видео:17 задание ОГЭ по математикеСкачать

Свойства квадрата

• Длины всех сторон квадрата равны.
• Все углы квадрата прямые.
• Диагонали квадрата равны.
• Диагонали пересекаются под прямым углом.
• Диагонали квадрата являются биссектрисами углов.
• Диагонали квадрата точкой пересечения делятся пополам.

Изложеннные свойства изображены на рисунках ниже:

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Диагональ квадрата

Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

.

(1)

Из равенства (1) найдем d:

.

(2)

Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.

Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:

Ответ:

Видео:Задание 26 Вписанный квадратСкачать

Окружность, вписанная в квадрат

Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):

Видео:Радиус описанной окружностиСкачать

Формула вычисления радиуса вписанной окружности через сторону квадрата

Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:

(3)

Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.

Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:

Ответ:

Видео:Задание 16 ОГЭ по математике. Окружность описана около квадратаСкачать

Формула вычисления сторон квадрата через радиус вписанной окружности

Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:

(4)

Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.

Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:

Ответ:

Видео:Задание 16 Часть 3Скачать

Окружность, описанная около квадрата

Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):

Видео:Длина окружности. Математика 6 класс.Скачать

Формула радиуса окружности описанной вокруг квадрата

Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.

Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:

(5)

Из формулы (5) найдем R:

(6)

или, умножая числитель и знаменатель на , получим:

.

(7)

Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.

Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:

Ответ:

Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

Формула стороны квадрата через радиус описанной около квадрата окружности

Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.

Из формулы (1) выразим a через R:

.

(8)

Пример 5. Радиус описанной вокруг квадрата окружности равен Найти сторону квадрата.

Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя в (8), получим:

Ответ:

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Периметр квадрата

Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:

(9)

где − сторона квадрата.

Пример 6. Сторона квадрата равен . Найти периметр квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя в (9), получим:

Ответ:

Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

Признаки квадрата

Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.

Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.

Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).

Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть

(10)

Так как AD и BC перпендикулярны, то

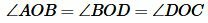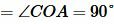(11)

Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда

(12)

Эти реугольники также равнобедренные. Тогда

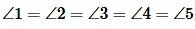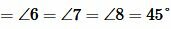(13)

Из (13) следует, что

(14)

Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).

Видео:Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать

Радиусы описанной и вписанной окружностей в квадрат

Видео:ЕГЭ профиль #3 / Радиус описанной окружности / прямоугольник / диагонали / решу егэСкачать

Окружность вписанная в квадрат

Чтобы формула нахождения радиуса вписанной окружности в квадрат r была правильно рассчитана, необходимо изначально вспомнить какими свойствами обладает данная фигура. У квадрата:

• все углы прямые, то есть, равны 90°;
• все стороны, как и углы, равны;
• диагонали равны, точкой пересечения бьются строго пополам и пересекаются под углом 90°.

При этом вписанная в выпуклый многоугольник окружность обязательно касается всех его сторон. Обозначим квадрат ABCD, точку пресечения его диагоналей O. Как видно на рисунке 1, пересечение линий АС и ВD дают равнобедренный треугольник АОВ, в котором стороны АО=ОВ, углы ОАВ=АВО=45°, а угол АОВ=90°. Тогда радиусом вписанной окружности в квадрат будет не что иное, как высота ОЕ полученного равнобедренного треугольника АОВ.

Если предположить, что сторона квадрата равна у, то формула нахождения радиуса вписанной окружности в квадрат будет выглядеть следующим образом:

Объяснение: в равнобедренном треугольнике АОВ высота ОЕ или радиус r делят основание АВ пополам (свойства), образовывая при этом прямоугольный треугольник с прямым угол ОЕВ. В маленьком треугольнике ЕВО основание ОВ образует со сторонами ОЕ и ЕВ углы по 45°. Значит треугольник ЕВО еще и равнобедренный. Стороны ОЕ и ЕВ равны.

Окружность описанная около квадрата

Вокруг квадрата также можно описать окружность. В этом случае каждая вершина фигуры будет касаться окружности. Следующая формула нахождения радиуса описанной окружности около квадрата будет находиться еще проще. В этом случае R описанной окружности будет равен половине диагонали квадрата. В буквенном виде формула выглядит так (рисунок 2):

Объяснение: после проведения диагоналей ABCD образовались два одинаковых прямоугольных треугольника АВС = CDA. Рассмотрим один из них. В треугольнике CAD:

• угол CDA=90°;
• стороны AD=CD. Признак равнобедренного треугольника;
• угол DAC равен ACD. Они равны по 45°.

Чтобы найти в этом прямоугольном треугольнике гипотенузу АС, необходимо воспользоваться теоремой Пифагора:
, отсюда
Поскольку окружность касается вершин квадрата, а точка пересечения его диагоналей является центром описанной окружности (свойства), то отрезок ОС и будет радиусом окружности. Он является половинкой гипотенузы. Это утверждение вытекает из свойств равнобедренного треугольника или свойств диагоналей квадрата. Потому формула нахождения радиуса описанной окружности около квадрата в нашем случае имеет следующий вид:

Поскольку AD=CD, а свойства квадратного корня позволяют вынести одно из подкоренных выражений, тогда формула приобретает вид:

Нахождения величины радиуса описанной окружности около квадрата при известной величине радиуса вписанной окружности.

• треугольник ОСЕ – равнобедренный и прямоугольный;
• ОЕ=ЕС=;
• ОЕС=90°;
• ЕОС=ОСЕ=45°;

Найти: ОС=?
Решение: в данном случае задачу можно решить, воспользовавшись либо теоремой Пифагора, либо формулой для R. Второй случай будет проще, поскольку формула для R выведена из теоремы.