Боковые стороны трапеции, описанной около окружности, равны 15 и 22. Найдите среднюю линию трапеции.
Суммы противоположных сторон описанного четырёхугольника равны. Суммы боковых сторон трапеции:
15 + 22 = 37
Тогда и сумма оснований равна 37. Средняя линяя равна половине суммы оснований:
37/2 = 18,5
Ответ: 18,5.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
- Трапеция. Формулы, признаки и свойства трапеции
- Основные свойства трапеции
- Сторона трапеции
- Формулы определения длин сторон трапеции:
- Средняя линия трапеции
- Формулы определения длины средней линии трапеции:
- Высота трапеции
- Формулы определения длины высоты трапеции:
- Диагонали трапеции
- Формулы определения длины диагоналей трапеции:
- Площадь трапеции
- Формулы определения площади трапеции:
- Периметр трапеции
- Формула определения периметра трапеции:
- Окружность описанная вокруг трапеции
- Формула определения радиуса описанной вокруг трапеции окружности:
- Окружность вписанная в трапецию
- Формула определения радиуса вписанной в трапецию окружности
- Другие отрезки разносторонней трапеции
- Формулы определения длин отрезков проходящих через трапецию:
- Боковые стороны трапеции, описанной около
- 📸 Видео
Видео:2113 Боковые стороны трапеции описанной около окружности равны 16 и 3 Найдите среднюю линию трапецииСкачать

Трапеция. Формулы, признаки и свойства трапеции
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
- Основы трапеции — параллельные стороны
- Боковые стороны — две другие стороны
- Средняя линия — отрезок, соединяющий середины боковых сторон.
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны
- Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам
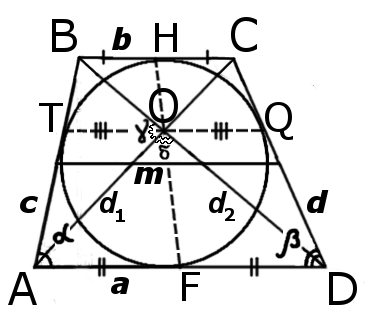 | 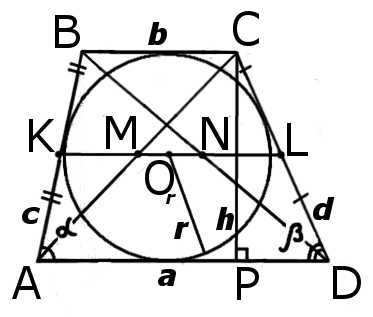 |
| Рис.1 | Рис.2 |
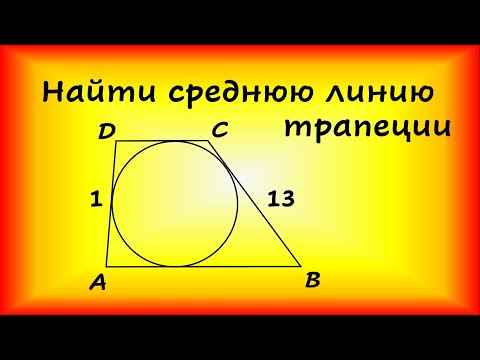
Видео:Боковые стороны трапеции, описанной около окружности, равны 13 и 1. Найдите среднюю линию трапеции.Скачать
Основные свойства трапеции
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
| m = | a + b |
| 2 |
BC : AD = OC : AO = OB : DO
d 1 2 + d 2 2 = 2 a b + c 2 + d 2
Видео:СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ #математика #егэ #shorts #профильныйегэСкачать

Сторона трапеции
Формулы определения длин сторон трапеции:
a = b + h · ( ctg α + ctg β )
b = a — h · ( ctg α + ctg β )
a = b + c· cos α + d· cos β
b = a — c· cos α — d· cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
| с = | h | d = | h |
| sin α | sin β |
Видео:№793. Боковые стороны трапеции равны 13 см и 15 см, а периметр равен 48 см. Найдите среднюю линиюСкачать
Средняя линия трапеции
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
| m = | a + b |
| 2 |
2. Формула определения длины средней линии через площадь и высоту:
| m = | S |
| h |
Видео:Около трапеции описана окружностьСкачать
Высота трапеции
Формулы определения длины высоты трапеции:
h = c· sin α = d· sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| 2 m | 2 m |
4. Формула высоты трапеции через площадь и длины оснований:
| h = | 2S |
| a + b |
5. Формула высоты трапеции через площадь и длину средней линии:
| h = | S |
| m |
Видео:2116 около окружности описана трапеция периметр которой равен 120 Найдите её среднюю линиюСкачать

Диагонали трапеции
Формулы определения длины диагоналей трапеции:
d 1 = √ a 2 + d 2 — 2 ad· cos β
d 2 = √ a 2 + c 2 — 2 ac· cos β
2. Формулы диагоналей через четыре стороны:
| d 1 = | √ | d 2 + ab — | a ( d 2 — c 2 ) |
| a — b |
| d 2 = | √ | c 2 + ab — | a ( c 2 — d 2 ) | a — b |
d 1 = √ h 2 + ( a — h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2
d 2 = √ h 2 + ( a — h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2
d 1 = √ c 2 + d 2 + 2 ab — d 2 2
d 2 = √ c 2 + d 2 + 2 ab — d 1 2
Видео:ЕГЭ математика 2023 Вариант 2 задача 1Скачать
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
| S = | ( a + b ) | · h |
| 2 |
3. Формула площади через диагонали и угол между ними:
| S = | d 1 d 2 | · sin γ | = | d 1 d 2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c 2 — | ( | ( a — b ) 2 + c 2 — d 2 | ) | 2 |
| 2 | 2( a — b ) |
5. Формула Герона для трапеции
| S = | a + b | √ ( p — a )( p — b )( p — a — c )( p — a — d ) |
| | a — b | |
где
| p = | a + b + c + d | — полупериметр трапеции. |
| 2 |
Видео:Задача про трапецию, описанную около окружностиСкачать

Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
Видео:Средняя линия трапеции, описанной около окружности.Скачать

Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p — a )( p — c )( p — d 1) |
где
| p = | a + c + d 1 |
| 2 |
a — большее основание
Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Окружность вписанная в трапецию
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
| r = | h |
| 2 |
Видео:Радиус описанной окружности трапецииСкачать

Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Боковые стороны трапеции, описанной около
27936. Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.
Средняя линия трапеции равна полусумме её оснований, значит:
Следовательно для нахождения средней линии трапеции необходимо найти сумму её оснований.
Воспользуемся свойством четырёхугольника описанного около окружности: известно, что суммы противолежащих сторон такого четырёхугольника равны.
Значит сумма боковых сторон трапеции равна сумме её оснований, то есть:

📸 Видео
Профильный ЕГЭ по математике. Задача 6. Боковые стороны трапеции, описанной около окружности...Скачать

ЕГЭ. Трапеция, описанная около окружности.Скачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

ЕГЭ Математика Задание 6#27936Скачать

Найти среднюю линию трапеции, зная большее основаниеСкачать

ЕГЭ Математика Задание 6#27937Скачать

Как найти СРЕДНЮЮ ЛИНИЮ трапеции по БОКОВЫМ сторонам?Скачать

Трапеция, вписанная в окружностьСкачать