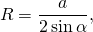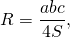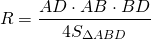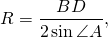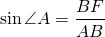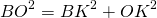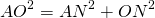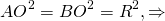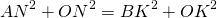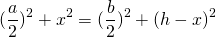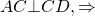Как найти расстояние от центра окружности до основания трапеции

Как найти радиус описанной окружности для трапеции?

В зависимости от данных условия, сделать это можно разными способами. Готовой формулы радиуса описанной около трапеции окружности нет.

I. Радиус описанной около трапеции окружности как радиус окружности, описанной около треугольника, вершины которого — вершины трапеции

Описанная около трапеции окружность проходит через все её вершины, следовательно, является описанной для любого из треугольников, вершины которых являются вершинами трапеции.

В общем случае радиус описанной около треугольника окружности может быть найден по одной из формул

где a — сторона треугольника, α — противолежащий ей угол;

либо по формуле

где a, b, c — стороны, S — площадь треугольника.

Для трапеции ABCD радиус может быть найден, например, как радиус окружности, описанной около треугольника ABD:

где синус угла A можно найти из прямоугольного треугольника ABF:

III. Радиус описанной около трапеции окружности как расстояние до точки пересечения серединных перпендикуляров

Радиус описанной окружности — точка пересечения серединных перпендикуляров с сторонам трапеции. (Можно рассуждать иначе: в равнобедренном треугольнике AOD (AO=OD=R) высота ON является также медианой. Для треугольника BOC — аналогично).

Если известна высота трапеции KN=h, основания AD=a, BC=b, можно обозначить ON=x.

Если центр окружности лежит внутри трапеции, OK=h-x, из прямоугольных треугольников ANO и BKO можно выразить

и приравнять правые части

Решив это уравнения относительно x, можно найти R.

IV. Если диагональ трапеции перпендикулярна боковой стороне, центр описанной окружности лежит на середине большего основания и радиус равен половине большего основания.

точка O — середина AD

Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной окружности лежит вне трапеции, за большим основанием.

I вариант нахождения радиуса для этого случая не изменяется.

Во II случае OK=h+x, соответственно, изменяется уравнение для нахождения x и R.

Позже рассмотрим конкретные задачи нахождения радиуса описанной около трапеции окружности.

Видео:Планиметрия 19 | mathus.ru| расстояние от центра окружности до точки пересечения диагоналей трапецииСкачать

В равнобедренную трапецию вписана окружность. Расстояние от центра окружности до точки пересечения диагоналей трапеции относится к радиусу, как 3 : 5. Найдите отношение периметра трапеции к длине вписанной окружности.

Пусть O — центр окружности, P — точка касания с боковой стороной AB, F и T — точки касания окружности с основаниями AD и BC, M — середина AB, K — точка пересечения диагоналей AC и BD трапеции. Обозначим OK = 3x, OP = 5x.

Поскольку AP : PB = AF : BT = AK : KC, то KP || BC || OM. Из прямоугольного треугольника OKP находим, что KP = 4x. Из подобия треугольников OKP и MPO находим, что

OM = = .

Тогда периметр трапеции равен 8OM = 50x. Следовательно, искомое отношение равно

= .

Ответ

.

Видео:ОГЭ ЗАДАНИЕ 16 РАДИУС ОКРУЖНОСТИ ВПИСАННОЙ В ТРАПЕЦИЮ РАВЕН 18. НАЙДИТЕ ВЫСОТУ ЭТОЙ ТРАПЕЦИИСкачать

Трапеция. Свойства трапеции

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .

Видео:Окружность и трапеция | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис Трушин +Скачать

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия –

Отношение площадей этих треугольников есть .

4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Видео:Задача про трапецию, описанную около окружностиСкачать

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Видео:10 класс, 19 урок, Расстояние от точки до плоскостиСкачать

Вписанная окружность

Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то

Видео:Отрезок, соединяющий середины диагоналей трапецииСкачать

Площадь

или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

📹 Видео

Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать

Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CDСкачать

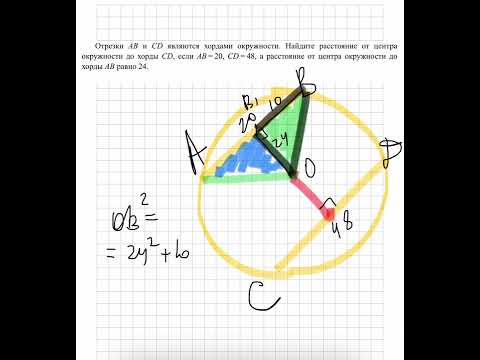
Планиметрия 27 | mathus.ru | окружность, касающаяся основания трапеции и вписанной в нее окружностиСкачать

Диагонали трапеции и точка их пересеченияСкачать

Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать

Длина хорды окружности равна 72 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Расстояние от точки пересечения диагоналей до основания трапеции (Задача №324600)Скачать

ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать

ОГЭ. Математика. Задание 26 | Прямоугольная трапеция и окружность | Борис Трушин |Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

✓ Как решить трапецию | ЕГЭ-2020. Задание 16. Профильный уровень. Основная волна | Борис ТрушинСкачать

Трапеция и вписанная окружностьСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

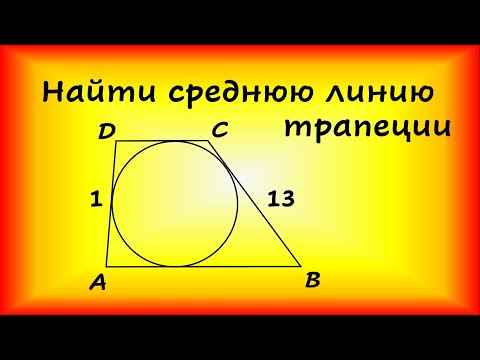
Боковые стороны трапеции, описанной около окружности, равны 13 и 1. Найдите среднюю линию трапеции.Скачать