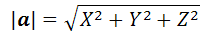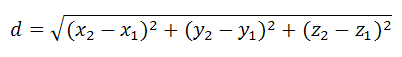Как найти расстояние между векторами (7 видео)

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Содержание

Система координат в пространстве
Плоскость в пространстве задается уравнением:
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Евклидово пространство
Определения
Свойства
Ортогонализация
Матричный формализм алгоритма Грама-Шмидта: QR-разложение
Расстояние от точки до многообразия
Вычисление расстояния
Угол между вектором и линейным многообразием
Свойства матрицы Грама
Задачи
Источник
Длина вектора Расстояние между двумя точками в пространстве
Длина вектора в пространстве
Расстояние между двумя точками в пространстве
3 комментария
🎦 Видео

Видео:Видеоурок "Расстояние между прямыми в пространстве"Скачать

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму:

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

То есть A + C + D = 0.

Аналогично для точки K:

Получили систему из трех уравнений:

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

Выразим C и B через A и подставим в третье уравнение:

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

Видео:Расстояние между точкамиСкачать

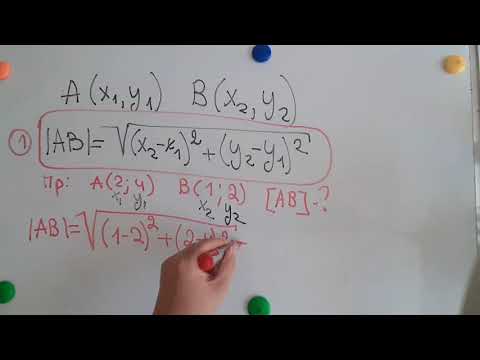
VMath

Инструменты сайта

Основное

Информация

Действия

Содержание

Видео:✓ Расстояние между скрещивающимися прямыми | ЕГЭ-2018. Задание 13. Математика | Борис ТрушинСкачать

Евклидово пространство

Одной из важнейших задач геометрии является задача измерения расстояния между двумя объектами. В произвольном линейном пространстве мы пока не можем определить насколько «близки» между собой объекты. В настоящем разделе понятие расстояния между двумя векторами — элементами линейного пространства — будет вводиться посредством скалярного произведения векторов. Насколько обоснован такой порядок введения понятий:

$ mbox qquad $ скалярное произведение $ to $ длина ?

Ведь в аналитической геометрии последовательность кажется более «естественной»: скалярное произведение двух векторов $ X_ $ и $ Y_ $ определялось как произведение длин этих векторов на косинус угла между ними: $ langle X,Y rangle = |X| cdot |Y| cdot cos (widehat) $. Тем не менее, формально непротиворечива и обратная схема: если допустить, что скалярное произведение любых двух векторов может быть как-то вычислено (например, в $ mathbb R^ $ по формуле $ langle X,Y rangle = x_1y_1+x_2y_2+x_3y_3 $ при заданных прямоугольных координатах $ (x_1,x_2,x_3) $ и $ (y_1,y_2,y_3) $ векторов $ X_ $ и $ Y_ $), то и длину векторов и угол между ними можно выразить через подходящие скалярные произведения: $$ |X|=sqrt,qquad widehat=arccos frac<sqrt> .$$

Видео:Расстояние между двумя точками. Координаты середины отрезка.Скачать

Определения

Вещественное линейное пространство $ mathbb E_ $ называется евклидовым 1) , если в этом пространстве определена функция, ставящая в соответствие паре векторов $ subset mathbb E $ вещественное число, называемое скалярным произведением векторов 2) $ X_ $ и $ Y_ $, и обозначаемое $ langle X,Y rangle_ $ или $ (X,Y)_ $; при этом фцнкция подчиняется аксиомам:

1. $ langle X,Y rangle= langle Y,X rangle $ для $ subset mathbb E $;
2. $ langle X_1+X_2,Y rangle = langle X_1,Y rangle + langle X_2,Y rangle $ для $ subset mathbb E $;
3. $ langle lambda, X,Yrangle=lambda, langle X,Yrangle $ для $ subset mathbb E, lambda in mathbb R $;
4. $ langle X,X rangle>0 $ для $ forall Xne mathbb O $, $ langle mathbb O,mathbb O rangle =0 $.

Из аксиом 1 и 2 вытекает свойство линейности скалярного произведения и по второму вектору:

2′. $ langle X,Y_1+Y_2 rangle = langle X,Y_1 rangle + langle X,Y_2 rangle $ для $ subset mathbb E $.

Пример 1. Пространство $ mathbb R_^ $, рассматриваемое как пространство вещественных векторов-столбцов. Для векторов

$$ X=left[begin x_1 \ vdots \ x_n end right] quad mbox quad Y=left[begin y_1 \ vdots \ y_n end right] $$ их скалярное произведение определим обобщением привычной из геометрии формулы $$ langle X,Y rangle = sum_^n x_jy_j = X^Y ; $$ в последней формуле $ ^ $ означает транспонирование. Будем называть это скалярное произведение стандартным. Легко проверить выполнимость аксиом 1 — 4 .

Однако стандартное определение скалярного произведения вовсе не является единственно допустимым; формально скалярное произведение можно ввести и другим способом. Рассмотрим (пока произвольную) вещественную квадратную матрицу $ A_ $ порядка $ n_ $ и положим $$ begin langle X,Y rangle = X^ A Y & = & a_x_1y_1+a_x_1y_2+ dots + a_x_1y_n &+ \ &+&a_x_2y_1+a_x_2y_2+ dots + a_x_2y_n &+ \ &+& dots &+ \ &+&a_x_ny_1+a_x_ny_2+ dots + a_x_ny_n & . end $$ (Здесь векторы $ X_ $ и $ Y_ $ из $ mathbb R_^ $ снова рассматриваются как столбцы.) Если матрица $ A_ $ является положительно определенной, то все аксиомы скалярного произведения будут удовлетворены.

Зачем нужна такая возможность в неоднозначности определения скалярного произведения в одном и том же пространстве? — Ответ на этот вопрос откладывается до следующего пункта. А пока приведу одно замечание 3) .

Пример 2. Пространство $ mathbb P_ $ полиномов одной переменной степеней $ le n_ $ с вещественными коэффициентами. Скалярное произведение полиномов

$$ p(x)=a_x^n+a_1x^+dots + a_n quad mbox quad q(x)=b_x^n+b_1x^+dots + b_n $$ введем формулой $$ langle p(x), q(x) rangle = sum_^n a_j b_j. $$ Легко проверить справедливость всех аксиом.

В том же пространстве $ mathbb P_ $ можно ли определить скалярное произведение формулой

$$ langle p(x),q(x) rangle = sum_^m p(x_k) q(x_k) quad npu _^m subset mathbb R ? $$

Пример 3. Линейное пространство $ mathbb R^ $ вещественных квадратных матриц порядка $ n_ $. Скалярное произведение введем формулой

Вторая интерпретация формулы связана с операцией $ operatorname $ нахождения следа матрицы, т.е. суммы элементов ее главной диагонали: $$ langle A,B rangle = operatorname left(Acdot B^ right) , . $$ Эквивалентность последнего представления определению устанавливается непосредственной проверкой.

На основании аксиом скалярного произведения, его вычисление для произвольных векторов $ X_ $ и $ Y_ $ может быть сведено к вычислению скалярных произведений векторов произвольного базиса. В самом деле, если система $ <X_1,dots,X_> $ составляет базис пространства $ mathbb E $, то, разложив оба вектора по этому базису $$X=x_1X_1+ dots +x_nX_n quad u quad Y=y_1X_1+ dots +y_nX_n , $$ получаем: $$langle X,Y rangle=langle x_1X_1+ dots +x_nX_n , y_1X_1+ dots +y_nX_n rangle=$$ $$ = left< begin &&x_1y_1 langle X_1,X_1 rangle + x_1y_2 langle X_1,X_2 rangle + dots + x_1y_n langle X_1,X_n rangle + \ &+&x_2y_1 langle X_2,X_1 rangle + x_2y_2 langle X_2,X_2 rangle + dots + x_2y_n langle X_2,X_n rangle+ \ &+ & dots qquad + \ &+&x_ny_1 langle X_n,X_1 rangle + x_ny_2 langle X_n,X_2 rangle + dots + x_ny_n langle X_n,X_n rangle end right> = $$ $$ =(x_1,x_2,dots,x_n)left( begin langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_n rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_n rangle \ dots & & & dots \ langle X_n,X_1 rangle & langle X_n,X_2 rangle & dots & langle X_n,X_n rangle end right) left(begin y_1 \ y_2 \ vdots \ y_n endright) . $$ Итак, при изменении векторов $ X_ $ и $ Y_ $ в последней формуле изменятся лишь строка и столбец координат, а промежуточная матрица останется неизменной. Задание этой матрицы, следовательно, полностью определит скалярное произведение в $ mathbb E_ $. Фактически задание скалярного произведения в разобранном выше примере пространства $ mathbb R^ $ по формуле $ langle X,Y rangle=X^AY $ можно рассматривать именно как частный случай этого при подходящем подборе базисных векторов. Согласно рассуждениям из примера $ 1_ $, матрица $$ left( begin langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_n rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_n rangle \ dots & & & dots \ langle X_n,X_1 rangle & langle X_n,X_2 rangle & dots & langle X_n,X_n rangle end right) $$ должна обладать некоторыми принципиальными свойствами. Так оно и окажется, см. ☟ НИЖЕ.

Матрицей Грама системы векторов 4) $ <X_1,dots,X_> $ называется квадратная матрица $$ G(X_1,dots,X_m)=left( begin langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \ dots & & & dots \ langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle end right) = left[ (X_j,X_k) right]_^m . $$ Ее определитель называется определителем Грама 5) (или грамианом) системы векторов $ <X_1,dots,X_> $: $$ (X_1,dots,X_m)=left| begin langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \ dots & & & dots \ langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle end right| = det left[ langle X_j,X_k rangle right]_^m . $$

С помощью матрицы Грама формула скалярного произведения записывается в виде $$ langle X,Y rangle =[x_1,dots,x_n] G(X_1,dots,X_n) left[ begin y_1 \ vdots \ y_n end right] . $$

Пример 4. В пространстве $ mathbb R^ $ столбцов из $ n_ $ элементов при стандартном способе задания скалярного произведения

$$ langle X,Y rangle = sum_^n x_jy_j quad npu quad X=[x_1,dots,x_n]<^>, Y=[y_1,dots,y_n]<^> $$ матрицу Грама системы векторов $ <X_j=[x_,x_,dots,x_]^ >_^m $ можно представить в виде произведения матриц $$ G(X_1,dots,X_)=left( begin x_ & x_ & dots & x_ \ x_ & x_ & dots & x_ \ dots & & & dots \ x_ & x_ & dots & x_ end right) left( begin x_ & x_ & dots & x_ \ x_ & x_ & dots & x_ \ vdots & & & vdots \ x_ & x_ & dots & x_ end right) . $$ Произведение имеет вид $ Mcdot M^ $ и, согласно теореме Бине-Коши, определитель этого произведения равен $ 0_ $ при $ m>n_ $ и неотрицателен при $ m le n $. НИЖЕ будет установлено, что обнаруженные свойства определителя Грама являются универсальными: они выполняются в произвольном евклидовом пространстве. См. также, «обращение» этого результата — задача 4 ☞ ЗДЕСЬ.

Видео:"Парадоксальное" среднее расстояние между точками на окружностиСкачать

Свойства

Теорема. Имеет место неравенство Коши–Буняковского:

$$ langle X,Y rangle ^2 le langle X,X rangle langle Y,Y rangle quad npu forall subset mathbb E . $$

Доказательство для случая $ mathbb R^_ $ приведено ☞ ЗДЕСЬ. Для доказательства общего случая используем одну вспомогательную конструкцию. Из аксиомы 4 следует, что для $ forall lambda in mathbb R $ будет выполнено $ langle lambda, X — Y,, lambda, X — Y rangle ge 0 $. Имеем: $$ 0 le langle lambda, X — Y,, lambda, X — Y rangle le lambda^2 langle X,X rangle — 2,lambda langle X,Y rangle +(Y,Y) . $$ Квадратное относительно $ lambda_ $ неравенство будет выполнено при всех вещественных значениях этого параметра тогда и только тогда, когда дискриминант квадратного трехчлена будет отрицателен: $$ mathcal D=langle X,Y rangle^2 — langle X,X rangle langle Y,Y rangle le 0 . $$ ♦

С помощью скалярного произведения, введенного в предыдущем пункте, можно доказать справедливость интегральной формы неравенства:

$$ left( int_a^b p(t)q(t) d,t right)^2 le int_a^b p^2(t) d,t cdot int_a^b q^2(t) d,t $$ для произвольных полиномов 6) $

subset mathbb R [x] $.

Длиною вектора $ X_ $ в евклидовом пространстве $ mathbb E_ $ называется число $$ |X| = sqrt ; $$ здесь квадратный корень понимается как корень арифметический: $ |X| ge 0 $. Расстоянием между векторами $ X_ $ и $ Y_ $ называется число $ |X-Y| $.

В $ mathbb R^_ $ при скалярном произведении, заданном стандартным способом формулой

$$ langle X,Y rangle = sum_^n x_jy_j quad npu quad X=[x_1,dots,x_n]<^>, Y=[y_1,dots,y_n]<^> , $$ длина вектора $ X_ $ определяется естественным (с точки зрения геометрии) способом: $ |X|=sqrt $.

Теорема. Имеет место неравенство треугольника

$$ |X+Y| le |X|+|Y| quad npu forall subset mathbb E . $$

Доказательство. На основании неравенства Коши-Буняковского, имеем: $$ 0 le langle X+Y,, X+Y rangle=langle X,X rangle+2langle X,Y rangle+langle Y,Y rangle le |X|^2+2, |X| cdot |Y| +|Y|^2=left(|X|+|Y| right)^2 . $$ ♦

Углом между векторами $ X_ $ и $ Y_ $ называется угол $$varphi = widehat = arccos frac .$$ Ввиду неравенства Коши-Буняковского это определение непротиворечиво: дробь под знаком арккосинуса не превосходит 1 по абсолютной величине. Векторы $ X_ $ и $ Y_ $ называются ортогональными: $ X bot Y $ если угол между ними равен $ pi/2 $, или, что то же, $ langle X,Y rangle=0 $.

Введенное таким определением понятие является естественным обобщением понятия угла на плоскости и в трехмерном пространстве. Хотя в пространствах размерностей больших $ 3_ $ человеческие мозги думать не приучены, тем не менее, абстракция находит практическое применение в задаче информационного поиска.

Пусть задача заключается в сравнении двух текстовых документов «на похожесть». Имеются некоторые наборы ключевых слов, описывающих каждый из этих документов. Составим объединение этих наборов, упорядочим получившийся набор (пронумеруем слова), посчитаем частоты вхождений каждого из слов в каждый из документов. Получим два вектора: $$ X_1=(f_,f_,dots), X_2=(f_,f_,dots) , $$ описывающие каждый из документов. Здесь $ f_ in $ — количество вхождений $ k_ $-го слова в $ j_ $-й документ. Для оценки близости векторов, на первый взгляд, кажется естественным вычислить расстояние между ними стандартным способом: $$ |X_1-X_2| = sqrt < sum_(f_-f_)^2> . $$ Однако, по здравому размышлению, понимаем, что при таком способе, документы различные по объему (общему количеству слов) будут слишком сильно отличаться друг от друга, при том, что могут оказаться близкими по сути (как будет отличаться большая статья от собственного реферата). Поэтому имеет смысл усреднить частоты в обоих текстах, т.е. рассматривать расстояние между векторами $ X_1/|X_1| $ и $ X_2/|X_2| $ единичной длины: $$ left|frac-fracright| = sqrt<2left( 1- frac right)> ; $$ скалярное произведение под знаком корня вычисляется стандартным способом: $ langle X_1,X_2 rangle=sum_ f_f_ $. Отсюда и возникает понятие косинусного расстояния: величина $$ frac $$ неотрицательна (поскольку компоненты векторов $ X_1,X_2 $ неотрицательны), и чем ближе она к $ 1_ $ тем меньше расстояние между между нормированными векторами. Эта величина называется также похожестью или cходством 8) векторов (документов) $ X_ $ и $ X_ $.

Теорема [Пифагор]. Если $ X bot Y $, то $ |X+Y|^2=|X|^2+|Y|^2 $.

Если векторы $ X_1,dots,X_k $ попарно взаимно ортогональны, то

Пример. Найти расстояние между полиномами

$$p(x)=x^-1/2,x^-1/2,x^+5,x^-5,x^+5,x^2+1 quad u quad q(x)=5,x^2+1 $$ если скалярное произведение задается формулой а) $ displaystyle langle p(x), q(x) rangle = sum_^ a_j b_j $ ; б) $ displaystyle langle p(x), q(x) rangle = int_^1 p(t)q(t) d, t $.

Решение. Для случая а) нам достаточно просто вычислить сумму квадратов коэффициентов разности $ p(x)-q(x) $: расстояние равно $ sqrt $.

Для случая б) нам придется иметь дело с интегралом $$ int_^1 left(p(t)-q(t) right)^2 d, t = int_^1 left(t^-1/2,t^-1/2,t^+5,t^-5,t^ right)^2 d, t , $$ который, несмотря на свой громоздкий вид, может быть вычислен элементарными приемами математического анализа. В этом случае расстояние будет равно $ sqrt $.

Ответ. а) $ approx 7.176 $ ; б) $ approx 0.076 $.

Теперь прокомментируем последний пример. В разделе, посвященном полиному одной переменной, имеется теорема о непрерывной зависимости корней полинома от его коэффициентов. Смысл этого результата в следующем: если коэффициенты полиномов

$$f(x)=x^n+a_1x^+dots+a_n quad u quad (x)=x^n+_1x^+dots+_n$$ из $ mathbb C[x] $ близки, то и корни этих полиномов (при соответствующей нумерации) будут близки на комплексной плоскости. В этой теореме мера близости полиномов оценивается по формуле $$ sqrt[n]<sum_^n|a_k-_k| gamma^ > quad npu quad gamma = max_<jin > left( sqrt[j] , sqrt[j]<|_j|> right) , $$ которая, хоть и не совпадает с формулой $$ sqrt<sum_^n left(a_k-_k right)^2> , $$ определяющей расстояние в пространстве полиномов, но идейно ей близка. Вычисленное в предыдущем примере расстояние между полиномами $ p_(x) $ и $ q_(x) $ по формуле а) оказывается достаточно большим в том смысле, что если для полинома $ p_(x) $ искать полином, имеющий почти такое же расположение корней на $ mathbb C_ $, то полином $ q_(x) $ окажется неподходящим кандидатом. 9)

Другое дело, если ставится задача приближения полинома $ p_(x) $ только на интервале $ [-1,1] $ — тогда полином $ q_(x) $ может оказаться вполне полезным. Выясним сначала природу интеграла, возникшего при решении. Пусть сначала $ p_(x) $ и $ q_(x) $ — произвольные, но (для простоты рассуждений) неотрицательные на интервале $ [a_,b] $ полиномы. Геометрический смысл интеграла $ int_a^b p(t) d, t $ — площадь криволинейной трапеции на плоскости $ (x_,y) $, ограниченной прямыми $ x=a_,,x=b,,y=0 $ и графиком $ y=p(x) $. Следовательно, геометрический смысл интеграла $$ int_a^b left| p(t)-q(t) right| d, t $$ — площадь фигуры, ограниченной прямыми $ x=a,,x=b_ $ и графиками $ y=p(x), y=q(x) $ 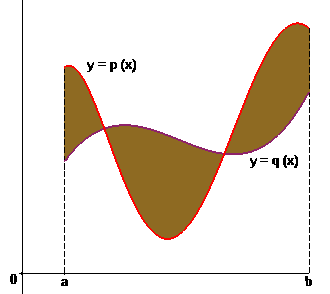(заштрихована коричневым на рисунке). Чем меньше эта площадь, тем «теснее» друг к другу на отрезке $ [a_,b] $ расположены графики $ y=p(x) $ и $ y=q(x) $. Величина $$ sqrt , $$ вообще говоря, не совпадает с предыдущей, но смысл ее тот же: она позволяет оценивать близость графиков на всем отрезке $ [a_,b] $. Ответ в примере для варианта б) позволяет заключить, что на отрезке $ [-1,1] $ полином $ p_(x) $ неплохо приближается своими младшими одночленами, т.е. на указанном отрезке график $ y=p(x) $ не должен слишком сильно отличаться от параболы $ y=5,x^2+1 $.

Подводя итог приведенным рассуждениям, можно только повторить: метод, выбираемый для оценки близости между объектами, может зависеть от поставленной задачи. Микроскоп не пригоден для наблюдения за большими объектами, а телескоп — за малыми.

Следующий результат также имеет название, взятое из планиметрии, где он формулируется так: сумма квадратов длин диагоналей параллелограмма равна сумме квадратов длин его сторон.

Теорема. В евклидовом пространстве имеет место равенство параллелограмма

$$ |X+Y|^2+|X-Y|^2 =2(|X|^2+|Y|^2) quad npu forall subset mathbb E . $$

Видео:Длина отрезкаСкачать

Ортогонализация

Пусть $ dim mathbb E=n $ и векторы $ $ составляют базис $ mathbb E_ $. Этот базис называется ортогональным если векторы попарно ортогональны: $ X_jbot X_k $; базис называется нормированным если каждый его вектор имеет единичную длину: $ |X_j|=1 $; базис называется ортонормированным если он ортогонален и нормирован, т.е. $$langle X_j,X_k rangle=delta_ ,quad npu quad subset .$$ Здесь $ delta_^ $ — символ Кронекера.

Ортогональный базис будем обозначать $ _1,dots, _n $.

Чему равно расстояние между двумя векторами ортонормированного базиса?

В пространстве $ mathbb R_^ $ стандартным ортогональным базисом является базис, состоящий из векторов $$ _j = big[underbrace_,0,dots,0big]^ quad npu quad j in . $$ Существование же ортогонального базиса в произвольном евклидовом пространстве еще требует доказательства. Предварительно установим следующий результат.

Теорема. Если ненулевые векторы $ X_1,dots, X_ $ попарно ортогональны, то они линейно независимы.

Доказательство. В самом деле, если $$ lambda_1 X_1 + dots + lambda_n X_n = mathbb O , $$ то, домножив это равенство скалярно на $ X_ $, получим $$ lambda_1 langle X_1,X_1 rangle + dots + lambda_n langle X_1,X_n rangle = 0 . $$ Поскольку $ langle X_1,X_j rangle=0 $ для $ jin $, то $ lambda_1 langle X_1,X_1 rangle=0 $, откуда $ lambda_1=0 $. Аналогично показывается, что и все остальные $ lambda_j $ равны 0. ♦

Задача. Пусть имеется произвольная система $ $ линейно независимых векторов. Требуется построить систему ортогональных векторов $ left<_1,dots, _k right> $ такую, чтобы линейные оболочки любых подсистем совпадали: $$ left(X_1,dots,X_m right) =left(_1,dots, _m right) quad npu quad min . $$ Иными словами, вектор $ _1 $ должен линейно зависеть от $ X_ $, вектор $ _2 $ должен линейно выражаться через $ X_1,X_2 $, $ _3 $ — через $ X_1,X_2,X_3 $ и т.д.

Алгоритм ортогонализации Грама — Шмидта 10)

В случае $ m_=1 $ возьмем $ _1=X_1 $: поскольку вектор $ X_ $ входит в линейно независимую систему , то $ _1 ne mathbb O $. Далее, будем искать $ _2 $ в виде $$_2=X_2 + alpha_ _1 $$ при пока неопределенном коэффициенте $ alpha_ $. Очевидно, что при таком выборе $ _2 $ условие $ (X_1,X_2)=(_1,_2) $ будет выполнено. Подберем $ alpha_ $ так, чтобы выполнялось $ _2 bot _1 $. $$0=langle _1,_2 rangle=langle _1,X_2 rangle+alpha_ langle _1,_1 rangle Rightarrow alpha_=-langle _1,X_2 rangle big/ langle _1,_1 rangle . $$ Таким образом, коэффициент $ alpha_ $, а вместе с ним и вектор $ _2 $ определяются единственным образом. При этом $ _2ne mathbb O $, ибо, в противном случае, векторы $ X_2 $ и $ _1=X_1 $ были бы л.з., что противоречит предположению о линейной независимости системы $ $. Продолжаем процесс далее: вектор $ _3 $ ищем в виде $$_3=X_3 + alpha_ _1 + alpha_ _2 $$ при пока неопределенных коэффициентах $ alpha_ $ и $ alpha_ $. Условие $ (X_1,X_2,X_3)=(_1,_2,_3) $ выполняется поскольку $$alpha_ _1 + alpha_ _2 in (X_1,X_2) subset (X_1,X_2,X_3) .$$ Подберем скаляры $ alpha_ $ и $ alpha_ $ так, чтобы выполнялось $ _3 bot _1 $ и $ _3 bot _2 $. Два этих условия задают систему линейных уравнений $$left< begin langle X_3,_1 rangle + alpha_ langle _1, _1 rangle + alpha_ langle _2 , _1 rangle &=0 ,\ langle X_3,_2 rangle + alpha_ langle _1, _2 rangle + alpha_ langle _2 , _2 rangle &=0 , end right. iff begin alpha_=-langle X_3,_1 rangle big/ |_1|^2 \ alpha_=-langle X_3,_2 rangle big/ |_2|^2 end $$

Процесс продолжается далее аналогично. Допустим, что векторы $ _1,dots,_ $ уже построены, они ненулевые, попарно ортогональные и $$ left(X_1,dots,X_ right)= left(_1,dots, _ right) .$$ Вектор $ _ $ ищем в виде: $$ _ =X_k+alpha_ _1 + alpha_ _2 +dots + alpha_ _ $$ при пока неопределенных коэффициентах $ alpha_,dots ,alpha_ $. Условие $ left(X_1,dots,X_,X_k right)= left(_1,dots, _,_ right) $ выполнено и, кроме того, $ _ne mathbb O $ (в противном случае $ X_k in left(_1,dots, _ right) =left(X_1,dots,X_ right) $, т.е. система $ <X_1,dots,X_,X_k > $ линейно зависима. Коэффициенты $ alpha_, dots ,alpha_ $ подбираются из условий $ _ bot _1,dots, _ bot _ $. Получающаяся система линейных уравнений имеет единственное решение $$alpha_=- langle X_k,_1 rangle big/ |_1|^2 ,dots, alpha_=-langle X_k,_ rangle big/ |_|^2 , $$ и это решение определяет единственный вектор $ _ $. ♦

Пример. Ортогонализовать систему векторов

$$ X_1=left[1,0,0,0,1 right], X_2=left[1,1,0,1,1 right], X_3=left[1,1,1,1,1 right] $$ при стандартном способе задания скалярного произведения в $ mathbb R^5 $.

Пример. Пусть в пространстве полиномов скалярное произведение задается формулой

$$ langle p(x),q(x) rangle=int_^ p(t)q(t) d, t .$$ Построить ортогональный базис этого пространства.

Решение. Искомый базис строится ортогонализацией канонического базиса $ 1,x,x^2,dots, x^n $. В результате получаем систему полиномов: $$1, x, x^2-frac, x^3-frac, x, x^4-frac, x^2+frac,dots $$ Полиномы, получающиеся из этих нормированием: $$P_0(x)=1, P_1(x)= x, P_2(x)=frac(3,x^2-1), P_3(x)= frac( 5,x^3-3, x), $$ $$ P_4(x)= frac(35,x^4-30, x^2+3),dots $$ $$ P_n(x)=frac sum_^ frac x^ $$ известны как полиномы Лежандра. Здесь $ lfloor mbox rfloor $ означает целую часть числа. Рекуррентное соотношение $$kP_(x)-(2k-1),xP_(x)+(k-1),P_(x) equiv 0, quad kge 2 ;$$ позволяет найти полином $ P_(x) $ если уже вычислены $ P_(x) $ и $ P_(x) $. ♦

В ортонормированном базисе пространства $ mathbb E_ $ матрица Грама из формулы скалярного произведения $$ langle X,Y rangle=(x_1,dots,x_n) G(X_1,dots,X_n) left( begin y_1 \ vdots \ y_n end right) $$ становится единичной и в таком базисе скалярное произведение становится стандартным : $$ langle X,Y rangle=sum_^n x_jy_j .$$

Следующая теорема устанавливает связь между двумя ортонормированными базисами в одном и том же пространстве.

Теорема. Матрица перехода от одного ортонормированного базиса к другому является ортогональной.

В пространстве $ mathbb R^_ $ матрица, составленная из столбцов произвольного ортонормированного базиса, является ортогональной.

Матричный формализм алгоритма Грама-Шмидта: QR-разложение

Рассмотрим пример из предыдущего пункта об ортогонализации системы векторов в $ mathbb R^5 $; только векторы будем рассматривать столбцами: $$ X_1=left[begin 1 \ 0 \ 0 \ 0 \ 1 end right], X_2=left[ begin 1 \ 1 \ 0 \ 1 \ 1 end right], X_3=left[ begin 1 \ 1 \ 1 \ 1 \ 1 end right] , . $$ Составим из них матрицу $$ A_ = left[ X_1,X_2,X_3 right] , . $$ Алгоритм Грама-Шмидта означает некоторые действия со столбцами этой матрицы, и эти действия могут быть записаны на языке матричного формализма, а именно — с помощью операции умножения этой матрицы на последовательность матриц определенного вида. В самом деле, на первом шаге алгоритма, «все остается на месте»: столбец $ _1 $ совпадает с $ X_ $, а оставшиеся столбцы мы пока не трогаем. Формально это «бездействие» можно записать с помощью умножения матрицы $ A_ $ на единичную матрицу порядка $ 3_ $. $$ Acdot E_ = left[_1,X_2,X_3 right] , . $$ Следующий шаг алгоритма уже менее тривиален: в получившейся матрице производятся действия над первыми двумя столбцами. При этом первый столбец остается неизменным, последний — тоже, а изменяется лишь второй: $$ _2 = X_2 + alpha_ _1 , . $$ Для получившейся на первом шаге матрицы, это действие эквивалентно домножению ее справа на матрицу $$ R_2 = left( begin 1 & alpha_ & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 end right) , . $$ Если значение $ alpha_ $ вычисляется как указано в алгоритме: $$alpha_=- langle _1,X_2 rangle big/ langle _1,_1 rangle =- langle X_1,X_2 rangle big/ langle X_1,X_1 rangle , , $$ то получившаяся матрица $$ Acdot E_ R_2 = left[_1,_2,X_3 right] $$ имеет первые два столбца ортогональными. Следующее преобразование получившейся системы столбцов равносильно домножению получившейся матрицы справа на матрицу вида $$ R_3 = left( begin 1 & 0 & alpha_ \ 0 & 1 & alpha_ \ 0 & 0 & 1 end right) , . $$ Если значения $ alpha_ $ и $ alpha_ $ вычисляются как указано в алгоритме, то получившаяся матрица $$ Acdot E_ R_2 R_3 = left[_1,_2,_3 right] $$ имеет систему своих столбцов ортогональной. Можно произвести еще одно дополнительное домножение $$ Acdot E_ R_2 R_3 cdot left( begin 1/langle _1,_1 rangle & 0 & 0 \ 0 & 1/langle _2,_2 rangle & 0 \ & 0 & 1/ langle _3,_3 rangle end right) , , $$ превратив полученную матрицу в матрицу с ортонормированной системой столбцов.

Теперь обдумаем полученный результат. Матрицы, на которые производились домножения матрицы $ A_ $ имеют довольно специфическую форму: они — либо диагональные, либо же отличаются от единичной матрицы в одном их своих столбцов. Эти матрицы могут быть отнесены к типу матриц элементарных преобразований системы столбцов произвольной матрицы $ A_ $. Все они являются верхнетреугольными, и их произведение $ R_ $ относится к тому же типу. Обратная к верхнетреугольной также является верхнетреугольной. В результате, можно получить разложение матрицы $ A_ $ в произведение $$ A=Q_R^ , , $$ где вторая матрица в произведении является верхнетреугольной, а первая имеет свои столбцы ортонормированными.

Теорема [о QR-разложении]. Для любой вещественной матрицы $ A_^ $ ранга $ n 11) $ tilde R_ $, такие, что $$ A=Q tilde R , . $$

Пример. Для матрицы из предыдущего примера имеем:

$$ left( begin 1 & 1 & 1 \ 0 & 1 & 1 \ 0 & 0 & 1 \ 0 & 1 & 1 \ 1 & 1 & 1 end right) = $$ $$ =left( begin 1/sqrt & 0 & 0 \ 0 & 1/sqrt & 0 \ 0 & 0 & 1 \ 0 & 1/sqrt & 0 \ 1/sqrt & 0 & 0 end right) left< left( begin 1 & -1 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 end right) left( begin 1 & 0 & -1 \ 0 & 1 & -1 \ 0 & 0 & 1 end right) left( begin 1/sqrt & 0 & 0 \ 0 & 1/sqrt & 0 \ 0 & 0 & 1 end right) right>^ $$ $$ = left( begin 1/sqrt & 0 & 0 \ 0 & 1/sqrt & 0 \ 0 & 0 & 1 \ 0 & 1/sqrt & 0 \ 1/sqrt & 0 & 0 end right)left( begin sqrt & sqrt & sqrt \ 0 & sqrt & sqrt \ 0 & 0 & 1 end right) , . $$ ♦

Для квадратной неособенной вещественной матрицы $ A_ $ матрица $ Q_ $ в QR-разложении будет ортогональной.

Последний результат имеет уже самостоятельное значение, не относящееся к материалам настоящего раздела. Например, его можно использовать для обращения матрицы $ A_ $. Дело в том, что ортогональная матрица обращается достаточно просто: $ Q^ = Q^ $.

Видео:19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

Расстояние от точки до многообразия

Задача. Найти расстояние от заданного вектора $ X_ $ до заданного множества $ mathbb Ssubset mathbb E $.

Такая постановка требует немедленного уточнения: что такое расстояние от вектора до множества? Обратясь за помощью к геометрии, мы можем ввести это понятие, основываясь на понятии расстояния между точками: например, расстояние от точки $ Xin mathbb R^2 $ до множества $ mathbb S subset mathbb R^2 $ определить как минимальное из возможных расстояний между точками $ X_ $ и $ Y_ $, где $ Yin mathbb S $. Следующий пример показывает, что наше определение оказывается ущербным.

Пример. Множество

Доказать следующие свойства операции $ perp $:

а) $ left(mathbb E_1^<^> right)^<^>=mathbb E_1 $; б) $ left(mathbb E_1 +mathbb E_2 right)^<^>=mathbb E_1^<^> cap mathbb E_2^<^> $; в) $ left(mathbb E_1 cap mathbb E_2 right)^<^>=mathbb E_1^<^>+mathbb E_2^<^> $.

Доказать, что в пространстве квадратных матриц со скалярным произведением, заданным формулой

$$ langle A,B rangle = operatorname left(Acdot B^ right) = sum_^n a_b_ , $$ подпространство кососимметричных матриц является ортогональным дополнением подпространства симметричных матриц.

Вычисление расстояния

Теорема $ 2 $ из предыдущего пункта позволяет сформулировать результат, на котором и будет основано решение задачи вычисления расстояния.

Теорема 1. Для любого вектора $ Xin mathbb E $ существует единственное представление его в виде $$ X=X^<^>+X^<^> quad npu X^<^>in mathbb E_1, X^<^> in mathbb E_1^<^> . $$

В этом разложении вектор $ X^<^> $ называется ортогональной проекцией вектора $ X_ $ на $ mathbb E_1 $, а вектор $ X^<^> $ — ортогональной составляющей вектора $ X_ $ относительно $ mathbb E_1 $ или же перпендикуляром, опущенным из точки $ X_ $ на подпространство $ mathbb E_1 $.

Теорема 2. Длина перпендикуляра, опущенного из точки $ X_ $ на подпространство $ mathbb E_1 $ , равна расстоянию от этой точки до подпространства: $$left|X^<^>right|=min_ |X-Y| . $$

Итак, задача, поставленная в начале ☞ ПУНКТА, решается вычислением $ left|X^<^> right| $. Для нахождения последнего числа сначала найдем базис $ $ подпространства $ mathbb E_1 $. Далее, ищем $ X^<^> $, принадлежащий $ mathbb E_1 $, в виде линейной комбинации базисных векторов: $$ X^<^>=alpha_1 X_1 + dots + alpha_k X_k . $$ Для нахождения скаляров $ alpha_1,dots , alpha_k $ используем тот факт, что вектор $ X^<^>=X-X^<^> $ должен быть ортогонален $ mathbb E_1 $, а значит, ортогонален каждому $ X_j $: $$langle X-X^<^>, X_j rangle =0 iff langle X^<^>, X_j rangle=langle X,X_j rangle . $$ Получаем систему линейных уравнений: $$ left< begin alpha_1 langle X_1,X_1 rangle &+ alpha_2 langle X_1,X_2 rangle &+ dots &+ alpha_k langle X_1,X_k rangle &= langle X,X_1 rangle, \ alpha_1 langle X_2,X_1 rangle & + alpha_2 langle X_2,X_2 rangle &+ dots &+ alpha_k langle X_2,X_k rangle &= langle X,X_2 rangle, \ dots & & & & dots \ alpha_1 langle X_k,X_1 rangle & + alpha_2 langle X_k,X_2 rangle &+ dots &+ alpha_k langle X_k,X_k rangle &= langle X,X_k rangle. end right. $$ с матрицей, которая нам уже известна как матрица Грама системы векторов: $ G(X_1,dots,X_k) $. Для однозначной разрешимости относительно $ alpha_1,dots , alpha_k $ необходимо и достаточно (см. ☞ теорема Кронекера-Капелли ), чтобы определитель этой матрицы — т.е. определитель Грама $ mathfrak G(X_1,dots,X_k) $ — был отличен от нуля.

Матрица Грама обращается в единичную если векторы $ X_1,dots,X_k $ входят в состав ортонормированного базиса пространства $ mathbb E_ $. Следовательно, по крайней мере в этом частном случае, система уравнений будет иметь единственное решение. В одном из последующих ☟ ПУНКТОВ будет установлен и более общий факт: $$ mathfrak(Y_1,dots,Y_k)=0 iff quad mbox quad quad mbox $$ Этот факт позволяет нам заключить, что, поскольку векторы $ $ — базисные для подпространства $ mathbb E_1 $, то система уравнений имеет единственное решение относительно $ alpha_1,dots , alpha_k $: $$alpha_1=alpha_1^,dots , alpha_k=alpha_k^ .$$ Теперь может быть найдена проекция вектора $ X_ $ на $ mathbb E_1 $: $$ X^<^>=alpha_1^ X_1 + dots + alpha_k^ X_k , $$ а затем и составляющая: $ X^<^>=X-X^<^> $.

Пример. Найти расстояние от точки $ X=[1,1,2,2,2] $ до подпространства

$$ mathbb E_1= left< Xin mathbb R^5 left| begin x_1&-x_2&-x_3&+x_4 & &= 0, \ 2,x_1&-x_2&-x_3&+2,x_4 &-x_5 &=0 end right. right> , $$ если скалярное произведение определяется стандартно: $ langle X,Y rangle=sum_^5 x_jy_j $.

Решение. Базис $ mathbb E_1 $ составляет фундаментальная система решений системы линейных уравнений, например: $$X_1=[0,-1,1,0,0], X_2=[-1,0,0,1,0], X_3=[1,1,0,0,1] .$$ Составляем матрицу Грама этой системы векторов и выписываем систему уравнений: $$ left( begin 2 & 0 & -1 \ 0 & 2 & -1 \ -1 & -1 & 3 end right) left( begin alpha_1 \ alpha_2 \ alpha_3 end right) = left( begin 1 \ 1 \ 4 end right) Rightarrow alpha_1=frac,, alpha_2=frac,, alpha_3=frac . $$ Ортогональная проекция вектора $ X_ $ на $ mathbb E_1 $: $$ X^<^>= frac X_1 + frac X_2 + frac X_3=left[frac,, frac,, frac,, frac,, frac right] , $$ а ортогональная составляющая вектора $ X_ $ относительно $ mathbb E_1 $: $$ X^<^>=X-X^<^>= left[frac,, frac,, frac,, frac,, — frac right] quad Rightarrow left|X^<^>right| =frac<sqrt> . $$

Ответ. $ 1/sqrt $.

Альтернативный способ вычисления расстояния от точки до линейного многообразия, заданного системой линейных уравнений ☞ ЗДЕСЬ.

Расстояние от точки $ X_ $ до линейного подпространства, базисными векторами которого являются $ X_1,dots,X_k $, вычисляется по формуле: $$ d=sqrt<frac<(X_1,dots,X_k, X)><(X_1,dots,X_k)>> . $$

Доказательство ☞ ЗДЕСЬ.

Пример. В пространстве полиномов с вещественными коэффициентами степеней не выше $ 5_ $ со скалярным произведением, заданным формулой

$$langle p(x),q(x) rangle = int_^1 p(t)q(t) d,t $$ найти расстояние от полинома $ p(x)= -x^5+x^3-3,x+1 $ до линейного подпространства четных полиномов.

Решение. Базис подпространства четных полиномов состоит, например, из $ 1,x^2,x^4 $. Имеем: $$ (1,x^2,x^4)=left| begin int_^1 1 cdot 1 d,t & int_^1 1 cdot t^2 d,t & int_^1 1 cdot t^4 d,t \ int_^1 1 cdot t^2 d,t & int_^1 t^2 cdot t^2 d,t & int_^1 t^2cdot t^4 d,t \ int_^1 1 cdot t^4 d,t & int_^1 t^2 cdot t^4 d,t & int_^1 t^4 cdot t^4 d,t end right|=left| begin 2 & 2/3 & 2/5 \ 2/3 & 2/5 & 2/7 \ 2/5 & 2/7 & 2/9 end right|=frac ; $$ $$ (1,x^2,x^4,p(x))=left| begin 2 & 2/3 & 2/5 & 2 \ 2/3 & 2/5 & 2/7 & 2/3 \ 2/5 & 2/7 & 2/9 & 2/5 \ 2 & 2/3 & 2/5 & 3632/495 end right|=frac . $$ Отношение полученных определителей даст квадрат расстояния: $$ d^2=2642/495 . $$ К этому же ответу можно было прийти и быстрее если заметить, что при заданном скалярном произведении любой четный полином ортогонален любому нечетному полиному. Следовательно для выделения у $ p(x) $ ортогональной составляющей относительно подпространства четных полиномов достаточно оставить в его каноническом виде только нечетные одночлены. Расстояние равно норме полинома $ p(x)-1 $. ♦

Подводя итог: определители Грама полностью решают задачу о вычислении расстояния от точки до линейного подпространства в любом евклидовом пространстве; этот результат легко обобщается на произвольное линейное многообразие.

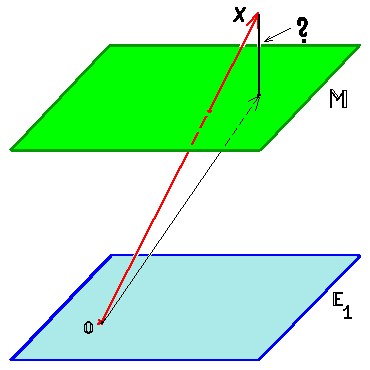
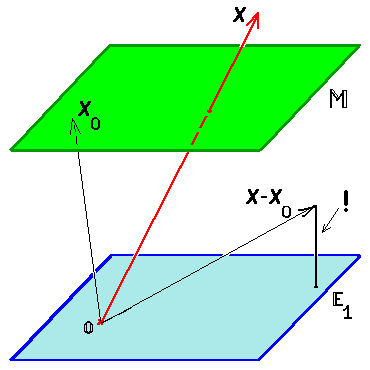
Теорема 3. Расстояние от точки $ X_ $ до линейного многообразия $ mathbb M=X_0+mathbb E_1 $ равно длине ортогональной составляющей вектора $ X-X_0 $ относительно подпространства $ mathbb E_1 $.

Доказательство. Геометрический смысл понятен из рисунков, иллюстрирующих решение проблемы в $ mathbb R^ $: надо свести задачу к случаю из предыдущей теоремы с помощью сдвига всей конструкции на вектор $ (-X_0) $.

Формальности: $$ min_ |X-Y| =min_ |X-(X_0+Z)|= min_ |(X-X_0)-Z)| . $$ Последняя величина — это расстояние от точки $ X-X_0 $ до $ mathbb E_1 $ ; согласно теореме $ 2 $ оно равно длине ортогональной составляющей вектора $ X-X_0 $ относительно $ mathbb E_1 $. ♦

Расстояние от точки $ X_ $ до линейного многообразия, заданного параметрически

Вычисление расстояния между линейными многообразиями (и некоторыми другими объектами, заданными алгебраическими уравнениями) ☞ ЗДЕСЬ.

Угол между вектором и линейным многообразием

Углом между вектором $ Xin mathbb E $ и линейным подпространством $ mathbb E_1 subset mathbb E $ назовем число — точную нижнюю грань множества углов между $ X_ $ и всевозможными векторами $ Y in mathbb E_1 $. Углом между вектором $ Xin mathbb E $ и линейным многообразием $ mathbb M=X_0+mathbb E_1 $ называется угол между $ X_ $ и $ mathbb E_1 $.

Теорема. Угол между вектором $ Xin mathbb E $ и линейным подпространством $ mathbb E_1 subset mathbb E $ равен углу между этим вектором и его ортогональной проекцией $ X^<^> $ на $ mathbb E_1 $.

Эта теорема сводит задачу к решенной в предыдущих пунктах задаче вычисления расстояния от вектора до подпространства, только теперь интерес смещается от ортогональной составляющей вектора к его ортогональной проекции.

Пример. Определить угол между вектором $ X_0=[1,0,3,0] $ и линейной оболочкой

Решение. Воспользуемся результатом, приведенным ☞ ЗДЕСЬ (для правильной стыковки рассматриваем все векторы как столбцы): $$ X_=L(L^ L_)^ L^ X_0 , . $$ Здесь $$ L=left(begin 5 & 1 & 2 \ 3 & 1 & -1 \ 4 & 4 & 1 \ -3 & 5 & 2 end right), qquad L^ L = left(begin 59 & 9 & 5 \ 9 & 43 & 15 \ 5 & 15 & 10 end right), $$ $$ (L^ L )^ = left(begin 41/2312 & -3/2312 & -2/289\ -3/2312 & 113/2312 & -21/289\ -2/289 & -21/289 & 307/1445 end right) $$ $$ L(L^ L_)^ L^= left(begin 9/10 & -1/5 & 1/5 & -1/10 \ -1/5 & 3/5 & 2/5 & -1/5 \ 1/5 & 2/5 & 3/5 & 1/5\ -1/10 & -1/5 & 1/5 & 9/10 end right), quad X_= left(begin 3/2 \ 1 \ 2 \ 1/2 end right) , . $$ $$ widehat<X_0,X_>=arccos frac <langle X_0,X_rangle ><sqrt< langle X_0,X_0rangle langle X_,X_ rangle>>= arccos frac<sqrt>= frac , . $$ ♦

Видео:Математика 6 Расстояние между точками координатной прямойСкачать

Свойства матрицы Грама

Теорема. $ (X_,dots,X_m)=0 $ тогда и только тогда, когда система векторов $ <X_,dots,X_m > $ линейно зависима.

Доказательство. Если система векторов $ <X_,dots,X_m> $ линейно зависима, то имеет место равенство $$alpha_1 X_1+alpha_2 X_2+dots+alpha_ X_=mathbb O$$ при некотором нетривиальном наборе скаляров $ alpha_1=alpha_1^,dots,alpha_m=alpha_m^ $. Домножим это соотношение (скалярно) на векторы $ X_1,X_2,dots,X_m $, получим систему уравнений, которую перепишем в матричном виде: $$ left( begin langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \ dots & & & dots \ langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle end right) left( begin alpha_1 \ alpha_2 \ vdots \ alpha_m end right)= left( begin 0 \ 0 \ vdots \ 0 end right) . $$ Если рассмотреть эту систему относительно переменных $ alpha_,dots,alpha_m $, то она оказывается однородной и, по предположенному, будет иметь нетривиальное решение $ alpha_1=alpha_1^,dots,alpha_m=alpha_m^ $ . Следовательно (см. ☞ ТЕОРЕМА КРОНЕКЕРА-КАПЕЛЛИ ) ее определитель равен нулю: $ (X_,dots,X_m)=0 $.

Обратно, если определитель Грама равен нулю, то предыдущая система имеет нетривиальное решение относительно $ alpha_,dots,alpha_m $. Пусть $ alpha_1=alpha_1^,dots,alpha_m=alpha_m^ $ — какое-то из этих решений. Составим вектор $$X^= alpha_1^ X_1+alpha_2^ X_2+dots+alpha_^ X_ $$ и вычислим скалярное произведение его на самого себя: $$ langle X^,X^ rangle = $$ $$ = (alpha_1^ ,alpha_2^ ,dots,alpha_m^ ) underbrace<left( begin langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \ dots & & & dots \ langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle end right) left(begin alpha_1^ \ alpha_2^ \ vdots \ alpha_m^ endright)>_<=mathbb O_>=0 . $$ Таким образом длина вектора $ X^ $ равна нулю, и, следовательно, по аксиоме 4 , сам вектор $ X^ $ — нулевой. Но тогда система векторов $ <X_,dots,X_m> $ линейно зависима. ♦

Ранг матрицы Грама совпадает с рангом системы порождающих ее векторов:

Если какой-то главный минор матрицы Грама обращается в нуль, то и все главные миноры бóльших порядков обращаются в нуль.

Теорема. $ (X_,dots,X_m) ge 0 $ для любого набора векторов $ <X_,dots,X_m > $.

Доказательство ☞ ЗДЕСЬ

Матрица Грама линейно независимой системы векторов является положительно определенной. Матрица Грама произвольной системы векторов является положительно полуопределенной.

Дальнейшие свойства матрицы и определителя Грама ☞ ЗДЕСЬ

Видео:РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ 10 и 11 классСкачать