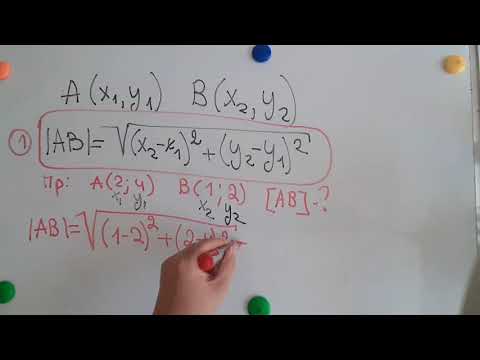Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол — это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Наименьшее расстояние между точкой и окружностью
Данный круг с данным радиусом имеет свой центр в определенной позиции в координатной плоскости. В координатной плоскости задается другая точка. Задача — найти кратчайшее расстояние между точкой и окружностью.
Примеры:
Подход :
который равен (др)
d = √ ((x2-x1) ^ 2 — (y2-y1) ^ 2)

Ниже приведена реализация вышеуказанного подхода:
// C ++ программа для поиска
// Наименьшее расстояние
// между точкой и
// круг
#include
using namespace std;
// Функция для поиска кратчайшего расстояния
void dist( double x1, double y1, double x2, double y2, double r)
cout «The shortest distance «
«between a point and a circle is «
sqrt (( pow ((x2 — x1), 2))
double x1 = 4, y1 = 6,
x2 = 35, y2 = 42, r = 5;
dist(x1, y1, x2, y2, r);
// Java-программа для поиска
// Наименьшее расстояние
// между точкой и
// круг
// Функция для поиска кратчайшего расстояния
static void dist( double x1, double y1, double x2,
double y2, double r)
System.out.println( «The shortest distance «
+ «between a point and a circle is «
+ (Math.sqrt((Math.pow((x2 — x1), 2 ))
+ (Math.pow((y2 — y1), 2 )))
public static void main(String[] args)
double x1 = 4 , y1 = 6 ,
x2 = 35 , y2 = 42 , r = 5 ;
dist(x1, y1, x2, y2, r);
/ * Этот код предоставлен PrinciRaj1992 * /
# Python программа для поиска
# Наименьшее расстояние
# между точкой и
# круг
# Функция поиска кратчайшего расстояния
def dist(x1, y1, x2, y2, r):
print ( «The shortest distance between a point and a circle is «
,((((x2 — x1) * * 2 ) + ((y2 — y1) * * 2 )) * * ( 1 / 2 )) — r);
dist(x1, y1, x2, y2, r);
# Этот код предоставлен 29AjayKumar
// C # программа для поиска кратчайшего расстояния
// между точкой и окружностью
// Функция для поиска кратчайшего расстояния
static void dist( double x1, double y1, double x2,
double y2, double r)
Console.WriteLine( «The shortest distance «
+ «between a point and a circle is «
+ (Math.Sqrt((Math.Pow((x2 — x1), 2))
+ (Math.Pow((y2 — y1), 2)))
public static void Main(String[] args)
double x1 = 4, y1 = 6,
x2 = 35, y2 = 42, r = 5;
dist(x1, y1, x2, y2, r);
/ * Этот код предоставлен PrinciRaj1992 * /
// PHP программа для поиска
// Наименьшее расстояние
// между точкой и
// круг
// Функция для поиска кратчайшего расстояния
function dist( $x1 , $y1 , $x2 , $y2 , $r )
echo «The shortest distance between a point and a circle is «
Видео:Расстояние между центрами. Окружность. Математика 10-11 классы.Скачать

Взаимное расположение точки и окружности
Видео:"Парадоксальное" среднее расстояние между точками на окружностиСкачать

Существует 3 варианта взаимного расположения точки и окружности:
Точка находится внутри круга, ограниченного окружностью:
Точка находится на окружности:
Точка находится вне круга, ограниченного окружностью:
Видео:Как найти расстояние между центрами | Олимпиадная математикаСкачать

Как отличить друг от друга эти варианты?
Вспомним определения окружности и круга:
Окружность — геометрическое место всех точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное неотрицательное расстояние, называемое её радиусом.
Круг — геометрическое место точек плоскости, расстояние от которых до заданной точки, называемой центром круга, не превышает заданного неотрицательного числа, называемого радиусом этого круга.
Из определений следует, что точка принадлежит окружности тогда и только тогда, когда расстояние между ней и центром равно радиусу, открытому кругу (так называют круг, в который не входит его граница) — когда расстояние меньше радиуса, лежит вне круга — когда расстояние больше радиуса. Картинка ниже подтвеждает это.
Итак, определение положения точки относительно окружности сводится к вычислению расстояния между двумя точками (данной точкой и центром окружности) и сравнению этой величины с радиусом.
Видео:Уравнение окружности и формула расстояния между точками на плоскостиСкачать

А как найти расстояние между двумя точками?
Точно так же, как длину отрезка или вектора с началом в одной из этих точек и концом в другой, — через теорему Пифагора.
Пусть координаты первой точки, А — (x_1) и (y_1), а второй, B — (x_2) и (y_2):
Построим прямоугольный треугольник с катетами, параллельными осям координат, и гипотенузой AB:
Катет OB в нём равен (x_2-x_1), катет OA — (y_1-y_2), значит, гипотенуза AB – корню из их суммы, т. е. [sqrt] Приведённая выше формула подходит для любых координат точек. Часто значения в скобках получаются отрицательными, в том числе и для катета OA в примере, но при возведении в квадрат знак теряется.
Ещё одна оговорка: при извлечении квадратного корня получается приближённое значение, которое может отличаться от привычного нам. Поэтому, если нам требуется сравнить расстояние с каким-то числом (что мы и собираемся сделать), удобнее не извлекать корень и сравнивать квадрат расстояния с квадратом числа.
Кстати, если вектор задан одной точкой, его длину можно определить по той же формуле, но чуть проще.
В самом деле, здесь (x_1=y_1=0), поэтому формула выглядит как [sqrt] Также ей можно пользоваться, когда одна из точек или один из концов отрезка находится в точке (0;0). Разумеется, здесь тоже действуют оговорки, описанные выше.
Видео:Найти расстояние между центрами описанной и вписанной окружностей в прямоугольном треугольникеСкачать
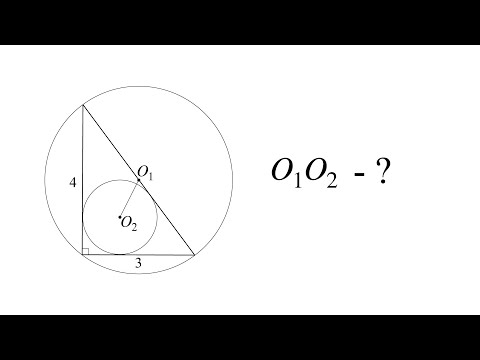
Формула
Теперь нетрудно вывести формулу, по которой можно определить взаимное расположение точки и окружности.
Если (px) и (py) — координаты точки, (ox) и (oy) — координаты центра окружности, (r) — радиус окружности, то
при ((ox-px)^2+(oy-py)^2lt) точка лежит внутри круга;
при ((ox-px)^2+(oy-py)^2=) точка лежит на окружности;
при ((ox-px)^2+(oy-py)^2gt) точка лежит вне круга.
Видео:Уравнение окружности (1)Скачать

Если лень читать
🔍 Видео
Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

9 класс, 6 урок, Уравнение окружностиСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Окружность и круг, 6 классСкачать

Планиметрия 5 | mathus.ru | расстояние между центрами окружностей в параллелограммеСкачать

Расстояние между центрами вписанной и описанной окружностей треугольника и их радиусами #ShortsСкачать

Планиметрия 11 |mathus.ru| расстояние между центрами пересекающихся окружностейСкачать

Расстояние между высотой и центром окружности (от точки до прямой) ОГЭ-ЕГЭСкачать

ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Окружность, диаметр, хорда геометрия 7 классСкачать

Планиметрия 12 | mathus.ru | расстояние между центрами пересекающихся окружностейСкачать

Из точки A проведены две касательные к окружности ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Расстояние между точкамиСкачать