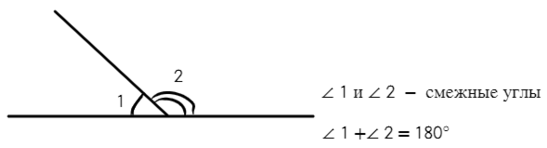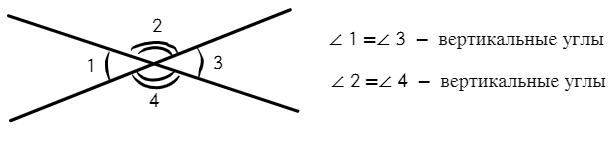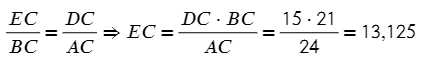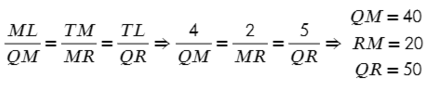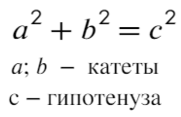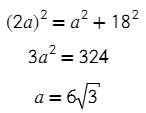Задачи применение свойств треугольника

Разделы: Математика

Цели урока:

• дидактические – совершенствование навыков решения задач на применение свойств прямоугольного треугольника;
• развивающие – развитие специального учебного навыка решения геометрических задач;
• воспитательные – воспитание интереса к математике.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Ход урока

1. Орг. момент.

Французский писатель Анатоль Франс однажды заметил: «Учиться можно только весело, чтобы переваривать знания, надо поглощать их с аппетитом». Так вот, давайте сегодня на уроке будем следовать этому совету писателя, будем активны, внимательны, будем поглощать знания с большим желанием.

Сегодня у нас заключительный урок по теме «Свойства прямоугольного треугольника».

Перед вами стоит задача – закрепить умение применять свойства прямоугольного треугольника при решении задач; проверить свои знания в ходе выполнения самостоятельной работы.

2. Актуализация опорных знаний.

Работа с буклетами( напротив каждого пункта «Памятки» записать правильный ответ)

1. Сумма двух острых углов прямоугольного треугольника равна 90°.
2. Катет прямоугольного треугольника, лежащий против угла в 30° равен половине гипотенузы.
3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
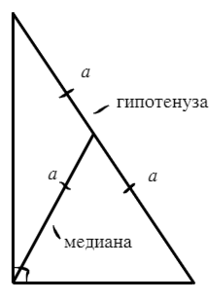
4. В прямоугольном треугольнике медиана, проведенная из вершины прямого угла, равна половине гипотенузы.
5. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

3. Решение задач.

а) по готовым чертежам ( готовые чертежи в буклетах и на интерактивной доске).

Устно.

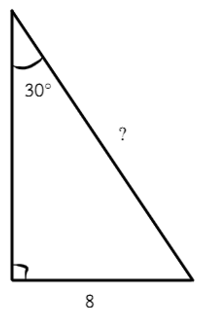
1. Найти: N

2. АВ=12см. Найти: ВС

3. PD = 1,2cм. Найти: PQ

Возле доски с решением.

4. АВ = 4,2см. ВС = 8,4см. Найти: B

5.DCM = 70° Найти: DAM

6. C = 90°, PC = СM; CA = 8 см Найти: MP.

б) Решение текстовых задач.

7. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего катета равна 18 см. Найдите гипотенузу и меньший катет.

Дано: ΔАВС, С=90°, А=60°, АВ+АС=18см Найти: АВ, АС. Решение: В=90° – 60°=30°, значит, АС – меньший катет, тогда АС=0,5АВ АВ+0,5АВ=18 АВ=12см, АС=6см Ответ: АВ=12см, АС=6см.

8. В прямоугольном треугольнике АВС С=90° и А=30°, проведена медиана СМ и биссектриса MD ΔСМА. Найдите MD, если ВС=23см.

Дано: ΔАВС, С=90°, А=30°, СМ-медиана С, МD – биссектриса ΔСМА, ВС=23см. Найти: MD. Решение: Т.к. СМ – медиана, то СМ-ВМ=МА=0,5АВ Т.к. А=30° и ВС=24см, то АВ=46см и = СМ=ВМ=МА=23см. Т.к. СМ=МА, то ΔСМА равнобедренный, следовательно, МD – высота. Т.к. А=30°, АDM= 90° и МА=23см, то MD=0,5МА= 11,5см. Ответ: MD=11,5см.

Физ.пауза

1. разминка шейного отдела позвоночника;
2. разминка для глаз.

4. Самостоятельная работа.

Прежде чем приступить к этой работе, запишем домашнее задание.

5. Итог урока.

Чем мы сегодня занимались на уроке?

Какие свойства применяли при решении задач?

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Решение задач на применение свойств прямоугольного треугольника.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Открытый урок по геометрии в 7 «Г» классе.

Тема урока: Решение задач на применение свойств прямоугольного треугольника.

Тип урока: обобщения и систематизации знаний.

систематизация, обобщение и расширение знаний и умений учащихся, связанных с применением свойств прямоугольных треугольников, устранение пробелов в знаниях учащихся по этой теме;

закрепление свойств прямоугольных треугольников для их практического применения к решению задач;

рассмотреть признак прямоугольного треугольника и свойство медианы прямоугольного треугольника;

формирование умения решать задачи на применение свойств прямоугольных треугольников;

формирование навыков в решении задач ОГЭ.

развитие умений анализировать условие задачи, строить логическую цепочку при решении задач, обоснованно делать выводы;

развитие умения переводить условие задачи на математический язык:

развитие познавательного интереса к геометрии:

развитие грамотной речи учащихся.

умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем;

воспитание внимательности, наблюдательности, положительного отношения к обучению.

знать формулировки свойств прямоугольных треугольников;

знать понятие прямоугольного треугольника, медианы треугольника;

уметь решать задачи на применение свойств прямоугольных треугольников;

уметь применять знания по изученной теме для решения задач ОГЭ;

1 Организационный этап урока.

Мотивационная беседа с учащимися – 3 мин.

Здравствуйте, ребята, садитесь. Надеюсь у вас хорошее настроение и вы готовы к уроку!? Тогда приступим. Какую тему мы изучали на последнем уроке? Правильно .

— составить предложение из следующих слов: задач, треугольников, применение, прямоугольных , решение, свойств, на.

— итак, тема урока: Решение задач на применение свойств прямоугольных треугольников.

— откройте тетради запишите тему урока.

Постановка учебной цели — 3 мин.

Эпиграф: «Познай самого себя» (Фалес Милетский).

— как вы понимаете слова Фалеса в контексте нашего урока?.

— отсюда вытекают цели урока.

Актуализация знаний- 5 мин

а) Работа в парах. Теоретический опрос-тест

Учитель. Для того чтобы вы проверили свои теоретические знания, вам предлагается тест . На работу с тестом – 5 минут.

1. Прямоугольным называется треугольник, у которого

все углы прямые;

два угла прямые;

один прямой угол;

нет верного ответа.

2. В прямоугольном треугольнике всегда

два угла острых и один прямой;

один острый угол, один прямой и один тупой угол;

все углы прямые;

один прямой и два тупых угла.

3. Стороны прямоугольного треугольника, образующие

прямой угол, называются

гипотенузой и катетом треугольника.

4. Сторона прямоугольного треугольника, противолежащая прямому углу, называется

нет верного ответа.

5. Сумма острых углов прямоугольного треугольника равна

6. Закончить теорему: В любом треугольнике против большей стороны лежит .

7. Закончить теорему: Если . одного прямоугольного треугольника соответственно равны . другого прямоугольного треугольника, то такие треугольники равны

один катет и прилежащий к нему угол; одному катету и прилежащему к нему углу

гипотенуза и один острый угол; гипотенузе и одному острому углу

катет и гипотенуза; катету и гипотенузе

три угла; трем углам

8. В прямоугольном треугольнике угол равен 36 градусов. Найти остальные углы треугольника.

9. Гипотенуза прямоугольного треугольника равна 20 см, а один из его острых углов 30 градусов. Найти длину катета, лежащего против этого угла.

10. Угол, лежащий напротив основания равнобедренного треугольника равен 80 градусов. Найти остальные углы треугольника .

Ответы: 3; 1; 2; 3; 3; 2; 3; 2; 4; 1.

Систематизация и коррекция знаний (решение задач на готовых чертежах)

Закрепление изученного материала.

Задача на «Применение свойства прямоугольного треугольника в повседневной жизни»

С наблюдательной вышки «А» ведется наблюдение за тонущей рыбачьей шхуной «В» и спасательным судном «С», движущимся к ней на помощь со скоростью 30 км/ч и находящимся от берега на расстоянии 3 км. Рыбачья шхун видна с вышки под углом 30 0 , а спасательное судно – под углом 60 0 к горизонту. Успеет ли судно вовремя подоспеть на помощь к шхуне, если по полученным сведениям, она может продержаться на поверхности воды около 25 минут.

1.ОАС, О = 90 0 , тогда ОАС = 90 0 — 60 0 = 30 0 .

САВ =60 0 – 30 0 =30 0 ,т.е. АСВ р/б, поэтому АС = ВС, ВС = 6 км.

3. = СВ : = = ч = 12 мин.

Доклад: «Применение свойства о сумме острых углов прямоугольного треугольника в повседневной жизни».

Свойство о сумме острых углов прямоугольного треугольника нашло широкое применение в транспортной, космической технике. Это свойство, например, лежит в основе конструкции простейшего уголкового отражателя. Так, уголковый отражатель, или КАТАФОТ, устанавливается на заднем крыле велосипеда для того, чтобы «возвращать» свет автомобильных фар. Это дает возможность водителю автомобиля видеть в темное время суток идущий впереди велосипед.

Катафот, установленный на спицах велосипедного колеса.

В настоящее время наше правительство уделяет большое внимание безопасности детей на дорогах. В школах на ранцы учащихся начальных классов наклеивают светоотражающие фликеры. Катафотные ткани или пленки называют фликерами — это не ткани в привычном смысле этого слова — это тонкие полимерные листы. Их поверхность обрабатывается таким образом, что на них получаются микроскопические пирамидки (уменьшенные копии уголкового отражателя). Именно благодаря этим микро пирамидкам катафотная ткань и отражает свет.

Световозвращатель может быть выполнен:

в виде тонкого полимерного листа (плёнки), обработанного особым образом. Обработка листа обеспечивает образование на его поверхности микроскопических пирамидок — уменьшенных копий уголкового отражателя ;

в виде световозвращающей полимерной ткани. Яркость отражённого света зависит от цвета ткани. Тёмные ткани поглощают больше света, светлые — больше отражают. Для большей износоустойчивости ткань могут запаивать в прозрачную полимерную (пластиковую) оболочку.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Применение

Предупреждающий жилет со световозвращающими полосами

Катафотные ткани используются, как элемент одежды, обуви, рюкзаков и др. для повышения безопасности на дорогах в тёмное время суток. Примеры: одежда дорожных рабочих, регулировщиков дорожного движения , спасателей , велосипедистов , детей.

Световозвращающие плёнки используются при изготовлении дорожных знаков .

Фликеры применяют для обозначения габаритов транспортных средств.

Наиболее широко катафоты применяются на велосипедном и автотранспорте для обозначения габаритов .

В ряде стран наличие фликера на пешеходе в тёмное время суток обязательно. В России, согласно ПДД , с 1 июля 2015 года вводится обязательным ношение светоотражающих элементов пешеходами в темное время суток вне населенных пунктов.

Задачи на «Применение свойств прямоугольного треугольника в ОГЭ».

1. Найти:
1) острые углы ΔАВС;
2) высоту СК, если ВС=3,8см.

2. В прямоугольном треугольнике СDЕ с прямым углом Е проведена высота ЕF. Найдите СF и FD, если CD=18см, а DCE=30°.

Вариант 2

1. Найти:
1) острые углы ΔАВС;
2) высоту СК, если ВС=5,6см.

2 . В прямоугольном треугольнике MNK с гипотенузой MN и углом M равным 60° проведена высота KН. Найдите MH и NН, если MН=6см.

Шёл мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележку с камнями для строительства. Мудрец остановил их и задал каждому по вопросу.

У первого спросил : “Что ты делал целый день?”. Тот с ухмылкой ответил, что целый день возил проклятые камни.

У второго спросил: “А что ты делал целый день?”. Тот ответил: “Я добросовестно выполнял свою работу”.

А третий улыбнулся, его лицо засветилось радостью и удовольствием:“А я принимал участие в строительстве храма”.

Пусть каждый сам оценит свою работу на уроке. (Сигнальные карточки)

Кто работал как первый человек? Поднимает синюю карточку.

Кто работал как второй человек? Поднимает зелёную карточку.

Кто работал как третий человек? Поднимает красную карточку.

Я желаю вам всегда работать с радостью и удовольствием. Спасибо вам за урок.

Урок окончен. До свидания!

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 958 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 310 человек из 70 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 679 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 552 848 материалов в базе

Материал подходит для УМК

«Геометрия», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

§ 3. Прямоугольные треугольники

Другие материалы

• 11.06.2020
• 332
• 6

• 26.05.2020
• 727
• 47

• 23.05.2020
• 202
• 5

• 06.05.2020
• 6491
• 222

• 28.04.2020
• 4193
• 76

• 12.04.2020
• 265
• 1

• 02.04.2020
• 126
• 0

• 01.04.2020
• 430
• 2

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 14.06.2020 3023
• DOCX 354.1 кбайт
• 214 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Кабановская Елена Евгеньевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 1 год и 8 месяцев
• Подписчики: 1
• Всего просмотров: 5065
• Всего материалов: 10

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Онлайн-семинар о развитии управляющих функций мозга ребенка

Время чтения: 1 минута

Петербургская учительница уволилась после чтения на уроке Введенского и Хармса

Время чтения: 3 минуты

У 76% российских учителей оклад ниже МРОТ

Время чтения: 2 минуты

У детей на портале госуслуг появятся собственные аккаунты

Время чтения: 1 минута

В Госдуме предложили ввести пост уполномоченного по правам учителей

Время чтения: 2 минуты

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Теория и задачи по треугольникам (Часть Ⅰ)

Вертикальные, смежные, соответственные, накрест лежащие углы.

Равенство и подобие треугольников.

Медиана, биссектриса, высота.

Кругом одна геометрия — круг друзей, квадрат врагов, треугольник любящих.

Давай на чистоту: геометрию трудно понимать, если не знаешь определенных теорем и свойств. Я постараюсь донести до тебя понятным языком только необходимое, а ты постарайся разобраться и запомнить!

Что такое луч, прямая, отрезок, угол, треугольник объяснять не буду, иначе кто-то уснет.

Когда небо было ярче, трава зеленее, а ты учился в 7 классе, началось знакомство с геометрией, туда и перенесёмся. Чтобы мы с тобой разговаривали на одном языке, начнем с равных углов.

Смежные углы — два угла, у которых одна сторона общая, а две другие расположены на одной прямой.

С вертикальными углами проще познакомиться на рисунке:

Такими дугами показываем равные углы ∠1 = ∠3 (одной дугой) и ∠2 = ∠4 (двумя дугами)

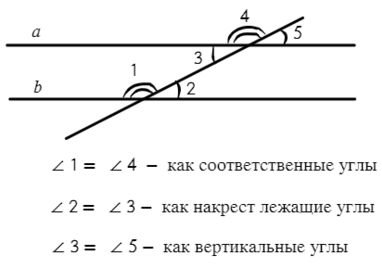
Теперь об углах при параллельных прямых (параллельные прямые — прямые, которые никогда не пересекутся, сколько бы их не продолжать. Лучше представить рельсы у путей на прямом участке):

Перейдем к фигурам, а именно к равенству треугольников:

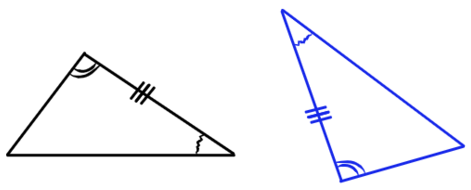
1) Треугольники, у которых две стороны и угол между ними соответственно равны двум сторонам и углу между ними другого треугольника, равны между собой.

Штрихом и двумя штрихами показывают одинаковые стороны, которые равны между собой. Аналогично равные углы показывает одинаковым количеством дуг. Крайне удобно показывать дано сразу на рисунке.

2) Треугольники, у которых два угла и сторона между ними соответственно равны двум углам и стороне между ними другого треугольника, равны между собой.

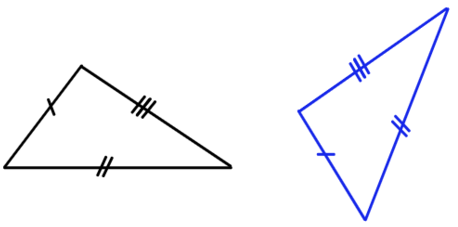
3) Треугольники, у которых три стороны соответственно равны трем сторонам другого треугольника, равны между собой.

Одинаковые треугольники — это идентичные между собой фигуры, только развернутые. У тебя же не возникает вопроса, равны ли эти телефоны? Ты смотришь на форму, модель и сразу говоришь — идентичны. Так же поступай с треугольниками, только на слово тебе никто не поверит, обязательно нужно доказать один из трех признаков, описанных выше.

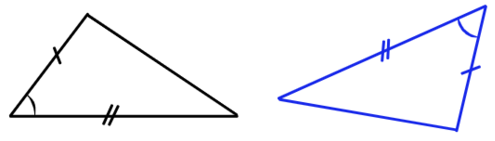
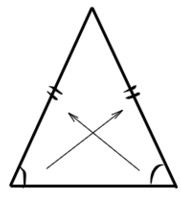
А вот эти фигуры какие?

Подобные! У них одинаковая форма, но разный размер. Тогда определим признаки подобных треугольников:

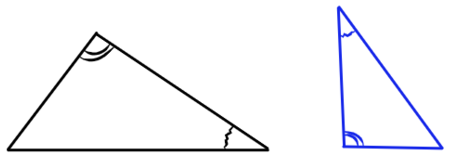
1) Если два угла одного треугольника соответственно равны двум углам другого, то эти треугольники подобны.

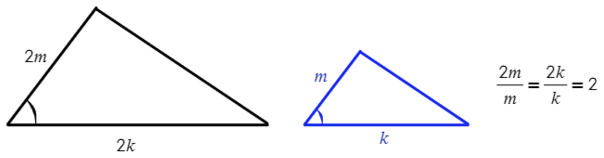
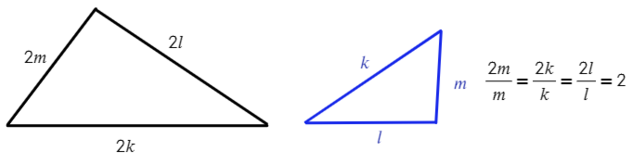
2) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то такие треугольники подобны.

3) Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Важное свойство: если в подобных треугольниках отношение сторон равно k, тогда площади этих треугольников будут относится, как k² (покажу на примере задачи №7).

Давай закрепим теорию в задачах.

Введем секретный шифр:

«Δ» означает треугольник

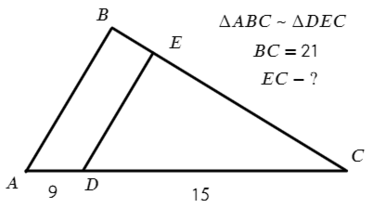
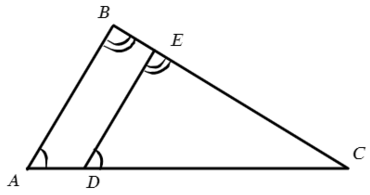
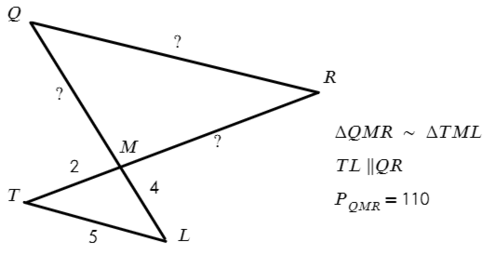
Задача №1. Дано на рисунке:

Т.к. треугольники подобны, запишем соотношения сторон против одинаковых углов.

AB II DE, значит ∠A = ∠EDC и ∠B = ∠DEC

Запишем тогда отношение сторон и выразим нужную сторону EC:

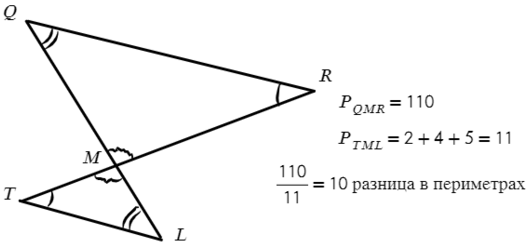
Задача №2. Дано на рисунке:

Периметр — это сумма всех сторон. Значит, если периметр отличается в 10 раз, то и стороны тоже в 10 раз.

Но мы же знаем, что все стороны должны отличаться в 10 раз, тогда:

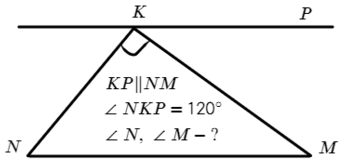
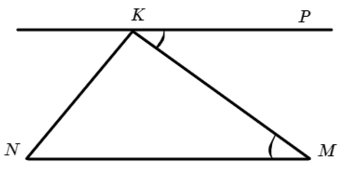
Задача №3. Дано на рисунке:

∠NKM = 90° и ∠NKP = 120°, значит ∠MKP = 30°

∠MKP = ∠KMN, как накрест лежащие углы при KP II NM => ∠KMN = 30°

А сумма углов в треугольнике 180° , да-да, не всегда, конечно, но Неевклидовая геометрию оставим на другой раз.

∠KNM = 180 − ∠NKM − ∠KMN = 60°

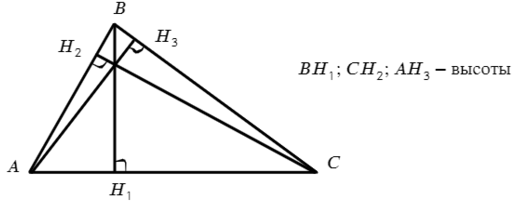
Теперь поговорим о самых распространенных отрезках в треугольнике: высота, биссектриса, медиана.

Высота — отрезок, опускающийся на прямую, содержащую противоположную сторону, под углом 90° (такой угол называется прямым).

Обратите внимание, что именно на прямую. В задаче №5 разберем почему.

Угол 90° обозначается таким квадратиком у пересечения с прямой.

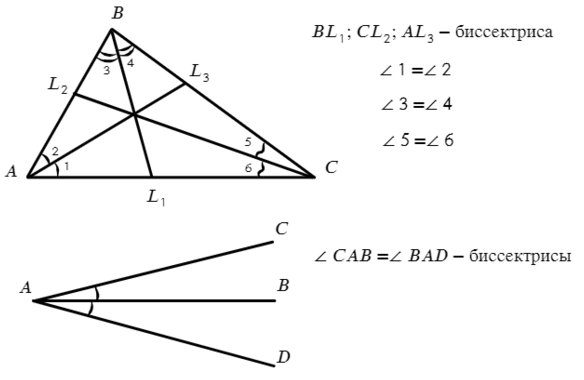
Биссектриса — луч, делящий угол, из которого выходит, пополам.

Запомнил, как обозначаем одинаковые углы? Одинаковым дугами.

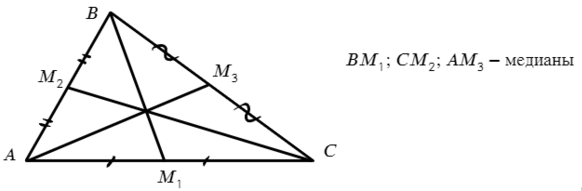
Медиана — отрезок, опускающийся из вершины треугольника на середину противоположной стороны.

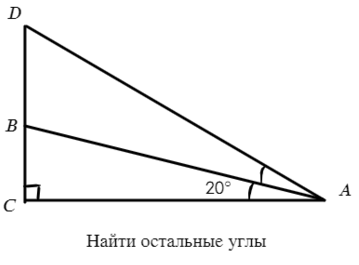
Задача №4. Дано на рисунке:

Давай посмотрим, что такое AB? АВ делит угол пополам (одинаковые дуги), значит, это биссектриса => ∠BAD = 20° => ∠CAD = 40°

В Δ CAD: ∠D = 180°− ∠C − ∠CAD = 50°, тогда

В Δ ВAD: ∠DBA = 180° − ∠D − ∠ВAD = 180° − 50° − 20° = 110°

∠DBA и ∠ABC — смежные (их сумма 180°) => ∠ABC = 180° − 110° = 70°

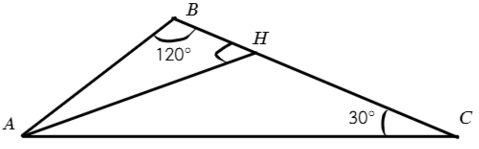
Задача №5. В ΔABC ∠B = 120°; ∠C = 30°. Из вершины А проведена высота, чему равен угол ∠BAH и ∠BAС?

Хороший рисунок — это 50% успеха, а в этой задаче все 90%. Рисуем треугольник примерно с углом 120°:

Рисунок получился плохой, а еще проблемы в ΔABH. Сумма углов должна быть 180°, но ∠B = 120° и ∠AHB = 90°, уже 210°! Что-то не так, вернемся к определению высоты — отрезок, опускающийся на прямую, содержащую противоположную сторону, под углом 90°.

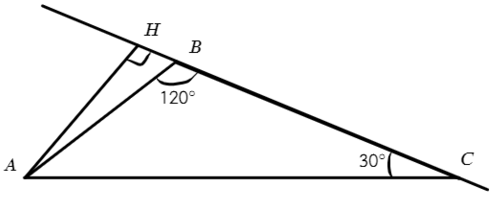
Тогда продлим сторону BC, а на нее опустим высоту. Высота получится вне треугольника:

В ΔBAH: ∠HBA = 60° (смежный с ∠ABC) => ∠BAH = 180° − 60° − 90° = 30°

В ΔABC: ∠BAC = 180° − 120° − 30° = 30°

Получается, что ∠BAC = ∠C = 30°, значит, этот треугольник равнобедренный. А что это такое?

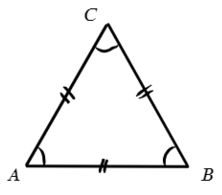
Равнобедренный треугольник — треугольник, у которого две стороны одинаковой длины. Такие стороны называют боковыми, а сторону, которая им не равна, основанием.

Есть пара крайне полезных свойств в равнобедренном треугольнике:

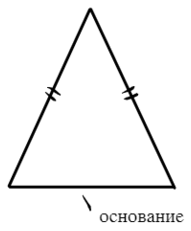
1) Углы при основании равнобедренного треугольника равны.

Против равных сторон лежат равные углы. Верно и обратное: если два угла у треугольника равны, то он равнобедренный

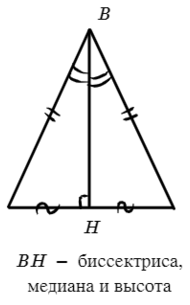
2) Медиана, проведенная к основанию треугольника, также является биссектрисой и высотой.

А что будет, если еще и третья сторона получится той же длины? Тогда этот треугольник равносторонний или правильный.

А чему равен каждый угол в равностороннем треугольнике? Сумма 180°, но все углы равны, они лежат против одинаковых сторон. Значит, один угол будет равен 180°/3 = 60°

А есть еще какие-то треугольники? Есть прямоугольный.

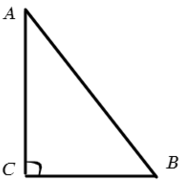
Прямоугольный треугольник — треугольник, у которого один угол равен 90° (прямой угол).

А два угла в треугольнике могут быть по 90°? Нет, тогда третьему углу останется 0°, нарисуешь такой?

1) Катет, лежащий против угла в 30°, равен половине гипотенузы.

Гипотенуза будет в два раза больше катета и равна 16.

2) Медиана, проведенная из прямого угла, равна половине гипотенузы.

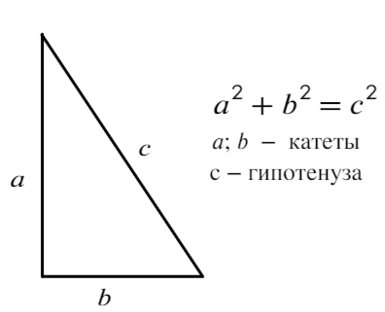
3) Теорема Пифагора

Теорема, которая встречается в 60% задач, а если дан прямоугольный треугольник — в 90%.

Квадрат гипотенузы (стороны против угла в 90°) равен сумме квадратов катетов.

Теорема Пифагора — это частный случай теоремы косинусов, но о ней мы потом поговорим.

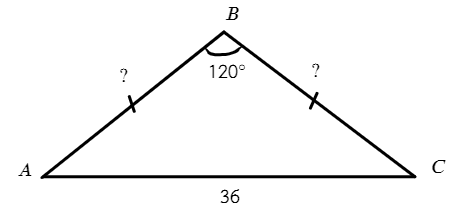
Задача №6. Дано на рисунке:

В ΔABC равнобедренный: ∠BAC = ∠BCA = 30°

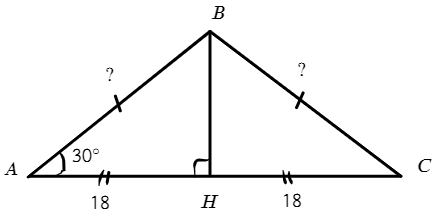
Опустим высоту из вершины В:

В равнобедренном треугольнике высота так же будет являться биссектрисой и высотой, значит AH = 18.

В ΔABH ∠A = 30°, скажем что BH = a, тогда AB = 2a. (против угла в 30° лежит катет в два раза больше гипотенузы)

В ΔABH по т. Пифагора:

Задача №7. ΔMNK ∼ ΔM₁N₁K₁. Площадь ΔMNK = 75, а площадь ΔM₁N₁K₁ = 225. Стороны соотносятся по названию. M₁N₁ = 9, чему равна MN

Вспомним про коэффициент подобия в площадях треугольника: если в подобных треугольниках отношение сторон равно k, тогда площади этих треугольников будут относится, как k²:

225/75 = 3 = k² => k = √3

M₁N₁/MN = k => MN = M₁N₁/k = 9/√3 = 3√3

Отлично, поздравляю тебя с Beginner ом по геометрии.

Если нашел опечатку, или что-то непонятно − напиши.

🎬 Видео

Слово пацана Задача на применение свойства средней линии треугольникаСкачать

Свойства прямоугольного треугольника. 7 класс.Скачать

Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Свойства равнобедренного треугольника. 7 класс.Скачать

Геометрия, 7 класс. Тема: "Решение задач на применение свойств прямоугольного треугольника".Скачать

Признаки равенства треугольников. 7 класс.Скачать

Средняя линия треугольника и трапеции. 8 класс.Скачать

7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Свойства прямоугольного треугольника. Практическая часть. 7 класс.Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Треугольники. Практическая часть - решение задачи. 7 класс.Скачать

Признаки равенства треугольников. Практическая часть. 7 класс.Скачать

Первый признак равенства треугольников. 7 класс.Скачать

Геометрия 7 класс (Урок№9 - Треугольник.)Скачать