Свойства касающихся окружностей внешним образом

Видео:ОГЭ № 25. "Окружности касаются внешним образом... "Скачать

Please wait.

Видео:Три окружности касаются прямой и друг друга внешним образомСкачать

We are checking your browser. mathvox.ru

Видео:Окружности касаются внешним образом #егэ2023 #математика #егэ #школа #shorts #fypСкачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:ОГЭ. Понятный разбор задачи №26. Две окружности радиусов 44 и 77 касаются внешним образом...Скачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6cd4ceb109d9149c • Your IP : 85.95.179.65 • Performance & security by Cloudflare

Видео:ОГЭ Задание 26 Внешнее касание двух окружностейСкачать

Касание окружностей

Говорят, что две окружности касаются, если они имеют единственную общую точку. Эта точка называется точкой касания окружностей. Касание окружностей бывает внутренним и внешним.

Видео:Пара касающихся окружностей | Осторожно, спойлер! | Борис Трушин |Скачать

Внутреннее касание

Касание называется внутренним, если центры окружностей лежат по одну сторону от точки касания окружностей. Построим две окружности, первая с центром A и радиусом AC, отметим на радиусе AC точку B, это будет центр второй окружности с радиусом BC:

Построенные окружности имеют только одну общую точку C. Говорят, что они касаются внутренним образом.

При внутреннем касании двух окружностей, расстояние между их центрами равно разности их радиусов.

Видео:9 класс, 8 урок, Взаимное расположение двух окружностейСкачать

Внешнее касание

Касание называется внешним, если центры окружностей лежат по разные стороны от точки касания. Построим две окружности, первая с центром A и радиусом AC, вторая с центром B и радиусом BC:

Построенные окружности имеют только одну общую точку C. Говорят, что они касаются внешним образом.

При внешнем касании двух окружностей, расстояние между их центрами равно сумме их радиусов.

Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

Взаимное расположение двух окружностей

Министерство образования и науки Российской Федерации

Муниципальное бюджетное общеобразовательное учреждение

города Новосибирска «Гимназия №4»

Секция: математика

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА

СВОЙСТВА ДВУХ КАСАЮЩИХСЯ ОКРУЖНОСТЕЙ

Учеников 10 класса:

Хазиахметова Радика Ильдаровича

Зубарева Евгения Владимировича

Л.Л. Баринова

Учитель математики

Высшей квалификационной категории

Содержание

§ 1.1 Взаимное расположение двух окружностей………………………. …………. ………3

§ 2 Свойства и их доказательства………………………………………..……………. ….…4

Многие задачи, включающие в себя две касающиеся окружности, можно решить более коротко и просто, зная некоторые свойства, которые будут представлены дальше.

Взаимное расположение двух окружностей

Для начала оговорим возможное взаимное расположение двух окружностей. Может быть 4 различных случая.

1.Окружности могут не пересекаться.

3. Касаться в одной точке снаружи.

4.Касаться в одной точке внутри.

§ 2. Свойства и их доказательства

Перейдем непосредственно к доказательству свойств.

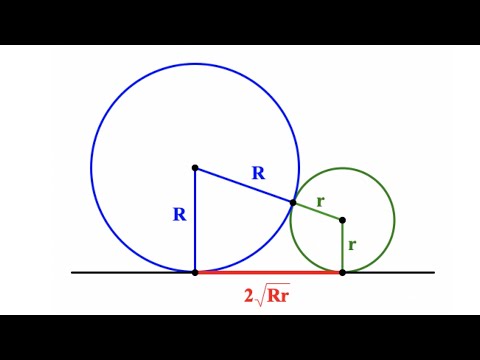
Отрезки между точками пересечения касательных с окружностями равны между собой и равны двум средним геометрическим радиусов данных окружностей.

Доказательство 1. О₁А₁ и О₂В₁ – радиусы, проведённые в точки касания.

(O₁D₂=(R+r) 2 -(R-r) 2 =R 2 +2Rr+r2-R 2 +2Rr-r 2 =√4Rr=2√Rr)

А₂В₂ = 2√Rr (доказывается аналогично)

Утверждения, используемые в доказательстве 1)Проведем радиусы в точки пересечения касательных с окружностями.

2)Эти радиусы будут перпендикулярны касательным и параллельны друг другу.

3)Опустим перпендикуляр из центра меньшей окружности к радиусу большей окружности.

4)Гипотенуза полученного прямоугольного треугольника равна сумме радиусов окружностей. Катет равен их разности.

5)По теореме Пифагора получаем искомое соотношение.

Точки пересечения прямой, пересекающей точку касания окружностей и не лежащей ни в одной из них, с касательными делят пополам отрезки внешних касательных, ограниченные точками касания, на части, каждая из которых равна среднему геометрическому радиусов данных окружностей.

Доказательство 1.МС = МА₁ (как отрезки касательных)

2.МС = МВ₁ (как отрезки касательных)

Утверждения, используемые в доказательстве Отрезки касательных, проведенных из одной точки к некоторой окружности равны. Используем это свойство для обеих данных окружностей.

Длина отрезка внутренней касательной, заключенного между внешними касательными, равна длине отрезка внешней касательной между точками касания и равна двум средним геометрическим радиусов данных окружностей.

Доказательство Этот вывод следует из предыдущего свойства.

Треугольник, образованный центрами касающихся окружностей и серединой отрезка касательной между радиусами, проведенными в точки касания, прямоугольный. Отношение его катетов равно частному корней радиусов этих окружностей.

Доказательство 1.МО₁ – биссектриса угла А₁МС, МО₂ – биссектриса угла В₁МС, т.к. центр окружности, вписанной в угол лежит на биссектрисе этого угла.

2.По пункту 1 ÐО₁МС + ÐСМО₂ = 0,5(ÐА1МС + ÐСМВ₁) = 0,5p = p/2

3.ÐО₁МО₂ – прямой. МС – высота треугольника O₁МО₂, т.к. касательная МN перпендикулярна радиусам, проведённым в точки касания → треугольники О₁МС и МО₂С – подобны.

4.О₁М / МО₂ = О₁С / МС = r / √Rr = √r / R (по подобию)

Утверждения, используемые в доказательстве 1)Центр окружности, вписанной в угол, лежит на биссектрисе этого угла. Катеты треугольника являются биссектрисами углов.

2)Пользуясь тем, что образованные таким образом углы равны, получаем, что искомый рассматриваемый нами угол прямой. Делаем вывод о том, что данный треугольник действительно прямоугольный.

3)Доказываем подобие треугольников, на которые высота (так как касательная перпендикулярна радиусам, проведенным в точки касания) делит прямоугольный треугольник, и по подобию получаем искомое отношение.

Треугольник, образованный точкой касания окружностей друг с другом и точками пересечения окружностей с касательной, прямоугольный. Отношение его катетов равно частному корней радиусов этих окружностей.

1. 2α + 2β + ÐА₁МС + ÐСМВ₁ = 2p → 2α + 2β = 2p — (ÐА₁МС + ÐСМВ₁) = 2p — p = p, α + β = p/2

Утверждения, используемые в доказательстве 1)Расписываем сумму углов треугольников, пользуясь тем, что они равнобедренные. Равнобедренность треугольников доказывается при помощи свойства о равенстве отрезков касательных.

2)Расписав сумму углов таким образом, получаем, что в рассматриваемом треугольнике есть прямой угол, следовательно он прямоугольный. Первая часть утверждения доказана.

3)По подобию треугольников(при его обосновании пользуемся признаком подобия по двум углам) находим отношение катетов прямоугольного треугольника.

Четырехугольник, образованный точками пересечения окружностей с касательной, является трапецией, в которую можно вписать окружность.

2.А₁А₂ ║ В₁В₂, т.к. равны соответственные углы, образованные при пересечении секущей А₁В_1.

1. А₁В₁ + А₂В₂ = 2√Rr + 2√Rr = 4√Rr = А₁А₂ + В₁В₂ → в трапеции А₂А₁В₁В₂ сумма оснований равна сумме боковых сторон, а это является необходимым и достаточным условием существования вписанной окружности.

Утверждения, используемые в доказательстве 1)Вновь воспользуемся свойством отрезков касательных. С его помощью докажем равнобедренность треугольников, образованных точкой пересечения касательных и точками касания.

2)Из этого будет следовать подобие данных треугольников и параллельность их оснований. На этом основании делаем вывод о том, что этот четырехугольник является трапецией.

3)По доказанному нами ранее свойству(2) находим среднюю линию трапеции. Она равна двум средним геометрическим радиусов окружностей. В полученной трапеции сумма оснований равна сумме боковых сторон, а это является необходимым и достаточным условием для существования вписанной окружности.

Рассмотрим на практическом примере, как можно упростить решение задачи, используя изложенные выше свойства.

В треугольнике АВС сторона АС=15 см. В треугольник вписана окружность. Вторая окружность касается первой и сторон АВ и ВС. На стороне АВ выбрана точка F, а на стороне ВС — точка М так, что отрезок FM является общей касательной к окружностям. Найдите отношение площадей треугольника BFM и четырехугольника АFМС, если FM — 4 см, а точка М отстоит от центра одной окружности на расстояние в два раза большее, чем от центра другой.

Дано: FM-общая касательная AC=15см FM=4см O₂M=2О₁M

2)2√Rr=4, √r/R=0,5 →r=1,R=4; PQ=FM=4

Задача 2

В равнобедренный треугольник АВС вписаны две касающиеся окружности с их общей точкой Д и проходящей через эту точку общей касательной FK. Найти расстояние между центрами этих окружностей, если основание треугольника АС = 9 см, а отрезок боковой стороны треугольника заключенный между точками касания окружностей равен 4 см.

Дано: ABC – равнобедренный треугольник; FK – общая касательная вписанных окружностей. АС = 9 см; NE = 4 см

Т.к. AFKC – равнобедренная трапеция, в которую вписана окружность, то ее высота равна среднему геометрическому ее оснований, т.е. (см) .

Тогда радиус большой окружности равен 3см. Но , следовательно , тогда (см).

А расстояние между центрами окружностей в данной задаче равно (см).

Ответ: см.

Задача 3

Окружности различных радиусов r и R с центрами О₁ и О₂ соответственно касаются внешним образом в точке К. Прямая касается этих окружностей в различных точках

А и В, а вторая прямая – в точках D и C соответственно. Докажите, что ABCD – описанная трапеция и найдите ее высоту.

Пусть прямые AB и CD пересекаются в точке О. Тогда ОА = ОD, ОВ = ОС, поэтому CD = = AB = 2√Rr

Точки О₁ и О₂ лежат на биссектрисе угла AOD. Биссектриса равнобедренного треугольника AOD является его высотой, поэтому AD ┴ O₁O₂ и BC ┴ O₁O₂ , значит,

AD ║ BC и ABCD – равнобедренная трапеция.

Отрезок MN – ее средняя линия, поэтому AD + BC = 2MN = 2AB = AB + CD

Следовательно, в эту трапецию можно вписать окружность.

Пусть AP – высота трапеции, прямоугольные треугольники АРВ и О₁FO₂ подобны, поэтому АР/О₁F = АВ/О₁О₂.

Отсюда находим, что

Список литературы

• Приложение к газете «Первое сентября» «Математика» №43, 2003 год
• ЕГЭ 2010. Математика. Задача С4. Гордин Р.К.

🎬 Видео

ЕГЭ задание 16Скачать

КАСАЮЩИЕСЯ ОКРУЖНОСТИСкачать

Задание 26 Две окружности, внешнее касаниеСкачать

Касающиеся окружности.Скачать

Касание окружностейСкачать

ОГЭ Задание 25 Внешнее касание двух окружностейСкачать

Интересное свойство касающихся окружностей с общей касательнойСкачать

КАСАЮЩИЕСЯ ОКРУЖНОСТИ. # ЕГЭ 2023Скачать

Геометрия Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружСкачать

Геометрия Две окружности радиусом R = 3 см и r = 1 см касаются внешним образом. Найти расстояние отСкачать

Две окружности разных радиусов касаются внешним образом в точке КСкачать

Длина общей внешней касательной двух внешне касающихся окружностей с разными радиусамиСкачать