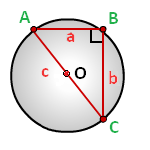
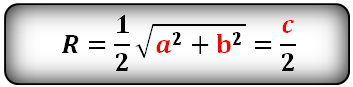Как найти радиус окружности по двум катетам (6 видео)

Радиус описанной окружности прямоугольного треугольника

Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.

a , b — катеты прямоугольного треугольника

c — гипотенуза

Формула радиуса описанной окружности прямоугольного треугольника (R):

Калькулятор — вычислить, найти радиус описанной окружности прямоугольного треугольника

Содержание

Нахождение радиуса описанной вокруг треугольника окружности
Формулы вычисления радиуса описанной окружности
Произвольный треугольник
Прямоугольный треугольник
Равносторонний треугольник
Примеры задач
Радиус описанной окружности около прямоугольного треугольника онлайн
1. Радиус окружности описанной около прямоугольного треугольника, если известна гипотенуза треугольника
2. Радиус окружности описанной около прямоугольного треугольника, если известны катеты треугольника
3. Радиус окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника
4. Радиус окружности описанной около прямоугольного треугольника, если известны катет и прилежащий острый угол треугольника
🎥 Видео

Видео:Сможешь найти радиус окружности? Окружность, вписанная в прямоугольный треугольникСкачать

Нахождение радиуса описанной вокруг треугольника окружности

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.

Видео:Как найти центр и радиус нарисованной окружности #математика #егэ2023 #школа #fyp #shortsСкачать

Формулы вычисления радиуса описанной окружности

Произвольный треугольник

Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:

где a, b, c – стороны треугольника, S – его площадь.

Прямоугольный треугольник

Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.

Равносторонний треугольник

Радиус описанной около правильного треугольника окружности вычисляется по формуле:

где a – сторона треугольника.

Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Примеры задач

Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.

Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:

Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:

Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.

Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:

Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.

Видео:Найти центр и радиус окружностиСкачать

Радиус описанной окружности около прямоугольного треугольника онлайн

С помощю этого онлайн калькулятора можно найти радиус описанной окружности около любого треугольника, в том числе радиус описанной окружности около прямоугольного треугольника. Для нахождения радиуса окружности описанной около треугольника введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Открыть онлайн калькулятор

Видео:Как найти радиус окружности, зная три отрезка | Денис ЖучковСкачать

1. Радиус окружности описанной около прямоугольного треугольника, если известна гипотенуза треугольника

Пусть известна гипотенуза c прямоугольного треугольника (Рис.1). Найдем радиус описанной окружности около треугольника.

Как найти радиус окружности по двум катетам

На странице Радиус окружности описанной около треугольника формула радиуса описанной окружности около треугольника по стороне и противолежащему углу имеет вид:

( small R=frac )

где C − угол противолежащий гипотенузе прямоугольного треугольника. Поскольку угол, противолежащий гипотенузе − прямой, то получим:

( small R=frac=frac, )

( small R=frac. )

(1)

Пример 1. Известна гипотенуза ( small с=frac ) прямоугольного треугольника. Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (1).

Подставим значение ( small c=frac ) в (1):

Ответ:

Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

2. Радиус окружности описанной около прямоугольного треугольника, если известны катеты треугольника

Пусть известны катеты a и b прямоугольного треугольника. Найдем радиус описанной окружности около треугольника (Рис.2).

Из теоремы Пифагора запишем формулу гипотенузы, выраженная через катеты:

( small c=sqrt. )

(2)

Подставляя (2) в (1), получим:

( small R=frac=frac<large sqrt>, )

( small R=frac<large sqrt>. )

(3)

Пример 2. Катеты прямоугольного треугольника равны: ( small a=15 , ; b=3.) Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около прямоугольного треугольника воспользуемся формулой (3). Подставим значения ( small a=15 , ; b=3) в (3):

Ответ:

Видео:Радиус описанной окружностиСкачать

3. Радиус окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника

Формула для вычисления радиуса окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника аналогична формуле вычисления радиуса описанной окружности около произвольного треугольника (см. статью на странице Радиус описанной окружности около треугольника онлайн):

(4)

Видео:Радиус и диаметрСкачать

4. Радиус окружности описанной около прямоугольного треугольника, если известны катет и прилежащий острый угол треугольника

Пусть известны катет a и прилежащий острый угол B прямоугольного треугольника (Рис.4). Найдем радиус описанной окружности около треугольника.

Так как треугольник прямоугольный, то сумма острых углов треугольника равна 90°:

( small angle A+angle B=90°. )

( small angle A=90°-angle B. )

(5)

Подставляя (5) в (4), получим:

( small R=frac=frac) ( small =frac )

( small R=frac. )

(6)

Пример 3. Катет прямоугольного треугольника равен: ( small a=15 ,) а прилежащий угол равен ( small angle B=25°. ) Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около прямоугольного треугольника воспользуемся формулой (6). Подставим значения ( small a=15 , ; angle B=25° ) в (6):