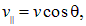- Сила Лоренца действующая на электрон
- Вычислить, найти силу Лоренца действующую на электрон или протон
- Радиус траектории электрона в магнитном поле
- Сила Лоренца действующая на протон
- Радиус траектории протона в магнитном поле
- Радиус движения электрона по окружности
- Электрон описывает в однородном магнитном поле окружность радиусом 4 мм. Скорость движения электрона равна 3,5 • 10^6м/с. Определите индукцию магнитного поля.
- Ваш ответ
- решение вопроса
- Похожие вопросы
- Шпаргалка по общей электронике и электротехнике.
- 5. ДВИЖЕНИЕ ЭЛЕКТРОНОВ В ОДНОРОДНОМ МАГНИТНОМ ПОЛЕ.
- Радиус движения электрона по окружности
- 5.3. Движение заряда в однородном магнитном поле
- 🌟 Видео
Видео:Урок 276. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

Сила Лоренца действующая на электрон
В частном случае носителем заряда является электрон. Тогда в формулу (5) в качестве Q следует подставить
При определении направления движения электронов с помощью правила левой руки следует учитывать, что направление движения электронов противоположно техническому направлению тока.
Величина и направление силы Лоренца определяются соотношением
где $vector$, $vector$ и $vector$ образуют правую систему.
Для электронов, движущихся перпендикулярно магнитному полю, формула упрощается:
Так как сила действует перпендикулярно скорости и направлению поля, она создает центростремительное ускорение, т.е. изменяет направление скорости, не меняя ее величины. Поэтому электрон движется в магнитном поле по окружности.
Видео:Физика - движение по окружностиСкачать

Вычислить, найти силу Лоренца действующую на электрон или протон
Видео:Радиус орбиты электронаСкачать

Радиус траектории электрона в магнитном поле
Для определения радиуса круговой траектории электрона приравняем силу Лоренца и центростремительную силу.
| r | радиус круговой траектории электрона, | метр |
|---|---|---|
| me | 9,11 · 10 -31 кг — масса электрона, | кг |
| e | 1,602 · 10 -19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость электрона, | м/с |
| B | магнитная индукция, | Тесла |
то, приравнивая обе силы, получаем
При больших значениях скорости (выше примерно 2 · 10 7 м/с) в расчетах нельзя использовать массу покоя электронов me, а необходимо учитывать релятивистское увеличение массы.
Видео:Движение электрона в магнитном поле.Скачать

Сила Лоренца действующая на протон
Электрический заряд протона равен по модулю заряду электрона, но имеет положительный знак.
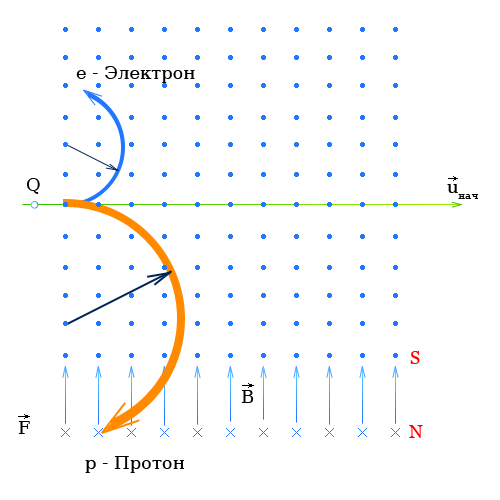
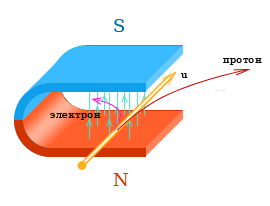
При определении направления движения протонов с помощью правила левой руки направление движения протонов совпадает с техническим направлением тока и с картинкой.
Таким образом электрон и протон влетая в магнитное поле в одном направлении будут отклоняться в разные стороны.
Величина силы действующая на электрон и на протон будет одинакова (определяется формулой №3), но поскольку протон гораздо тяжелее электрона, радиус закручивания для протона будет больше.
Видео:Правило рук 👋 КАК ЛЕГКО определять НАПРАВЛЕНИЕ ЛИНИЙ МАГНИТНОГО ПОЛЯ??Скачать

Радиус траектории протона в магнитном поле
| r | радиус круговой траектории протона, | метр |
|---|---|---|
| mp | 1,67 · 10 -27 кг — масса протона, | кг |
| p | 1,602 · 10 -19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость протона, | м/с |
| B | магнитная индукция, | Тесла |
Радиус траектории для протона будет вычисляться по аналогичной формуле
Из этой формулы видно что при одинаковых скоростях электрона и протона радиус траектории протона будет значительно больше, чем у электрона пропорционально отношению масс этих частиц
Аналогично при больших значениях скорости (выше примерно 2 · 10 7 м/с) в расчетах нельзя использовать массу покоя протонов mp, а необходимо учитывать релятивистское увеличение массы.
Видео:Движение заряженной частицы в магнитном поле | Физика ЕГЭ с Никитой АрхиповымСкачать

Радиус движения электрона по окружности
Видео:Камень брошен горизонтально, надо искать радиус кривизны траектории. (Волькенштейн 1.20)Скачать

Электрон описывает в однородном магнитном поле окружность радиусом 4 мм. Скорость движения электрона равна 3,5 • 10^6м/с. Определите индукцию магнитного поля.
Видео:Движение электронов в магнитном поле - Сила ЛоренцаСкачать

Ваш ответ
Видео:Определение шага винтовой линииСкачать

решение вопроса
Видео:Движение заряженной частицы в магнитном поле 2021-1Скачать

Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,857
- разное 16,824
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:КАК НАЙТИ РАДИУС КРУГА (ОКРУЖНОСТИ), ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

Шпаргалка по общей электронике и электротехнике.
Видео:Движение заряженных частиц Лекция 9-2Скачать

5. ДВИЖЕНИЕ ЭЛЕКТРОНОВ В ОДНОРОДНОМ МАГНИТНОМ ПОЛЕ.
В некоторых электровакуумных приборах используется движение электронов в магнитном поле.
Рассмотрим случай, когда электрон влетает в однородное магнитное поле с начальной скоростью v0, направленной перпендикулярно магнитным силовым линиям. В этом случае на движущийся электрон действует так называемая сила Лоренца F, которая перпендикулярна вектору нО и вектору напряженности магнитного поля Н. Величина силы F определяется выражением: F= еv0Н.
При v0 = 0 сила Рравна нулю, т. е. на неподвижный электрон магнитное поле не действует.
Сила F искривляет траекторию электрона в дугу окружности. Поскольку сила F действует под прямым углом к скорости нО, она не совершает работы. Энергия электрона и его скорость не изменяются по величине. Происходит лишь изменение направления скорости. Известно, что движение тела по окружности (вращение) с постоянной скоростью получается благодаря действию направленной к центру центростремительной силы, которой именно и является сила F.
Направление поворота электрона в магнитном поле в соответствии с правилом левой руки удобно определяется по следующим правилам. Если смотреть в направлении магнитных силовых линий, то электрон движется по часовой стреле. Иначе говоря, поворот электрона совпадает с вращательным движением винта, который ввинчивается по направлению магнитных силовых линий.
Определим радиус r окружности, описываемой электроном. Для этого воспользуемся выражением для центростремительной силы, известным из механики: F = mv20/r. Приравняем его значению силы F = еv0Н: mv20/r = еv0Н. Теперь из этого уравнения можно найти радиус: r= mv0/(еН).
Чем больше скорость электрона v0, тем сильнее он стремится двигаться прямолинейно по инерции и радиус искривления траектории будет больше. С другой стороны, с увеличением Н растет сила F, искривление траектории возрастает и радиус окружности уменьшается.
Выведенная формула справедлива для движения в магнитном поле частиц с любыми массами и зарядом.
Рассмотрим зависимость rот mи е. Заряженная частица с большей массой mсильнее стремится лететь по инерции прямолинейно и искривление траектории уменьшится, т. е. rстанет больше. А чем больше заряд е, тем больше сила F и тем сильнее искривляется траектория, т. е. ее радиус становится меньше.
Выйдя за пределы магнитного поля, электрон дальше летит по инерции по прямой линии. Если же радиус траектории мал, то электрон может описывать в магнитном поле замкнутые окружности.
Таким образом, магнитное поле изменяет только направление скорости электронов, но не ее величину, т. е. между электроном и магнитным полем нет энергетического взаимодействия. По сравнению с электрическим полем действие магнитного поля на электроны является более ограниченным. Именно поэтому магнитное поле применяется для воздействия на электроны значительно реже, нежели электрическое поле.
Видео:55. Движение частиц в электромагнитных поляхСкачать

Радиус движения электрона по окружности
Электрон, ускоренный разностью потенциалов U = 1 кВ, влетает в однородное магнитное поле, направление которого перпендикулярно к направлению его движения. Индукция магнитного поля В = 1,19 мкТл. Найти радиус R окружности, по которой движется электрон.
Дано:
U = 1 кВ = 10 3 В
В = 1,19 мкТл = 1,19 ·10 -6 Тл
Решение:
На электрон, движущейся в магнитном поле
действует сила Лоренца

которая является центростремительной
Т. к. движение электрона происходит по окружности, то
Радиус R окружности, по которой движется электрон, будет равен
Скорость электрона найдем из закона сохранения энергии
Ответ:
Видео:Физика - Магнитное полеСкачать

5.3. Движение заряда в однородном магнитном поле
Если начальная скорость заряженной частицы v перпендикулярна магнитному полю В, то в этом случае частица под действием силы Лоренца будет двигаться по окружности постоянного радиуса R (рис. 5.13)
Рис. 5.13. Движение отрицательно заряженной частицы в однородном магнитном поле
Сила Лоренца FL, направленная по радиусу к центру окружности, вызывает радиальное ускорение. По второму закону Ньютона имеем
следовательно, можем записать уравнение
из которого легко получить выражение для угловой скорости частицы
Если q, m и B — постоянные величины, то угловая скорость, а следовательно, и период
тоже являются постоянными величинами, не зависящими от энергии частицы. От скорости движения частицы зависит только радиус орбиты
Сила Лоренца создает только нормальное ускорение и, соответственно, направлена к центру окружности. Следовательно, направление вращения положительно заряженной частицы таково, что вращающийся в том же направлении винт будет двигаться против направления поля. Отрицательно заряженная частица вращается в противоположном направлении (см. рис. 5.14, 5.15).
Рис. 5.14. Движение положительно и отрицательно заряженных частиц в однородном магнитном поле.
Направление магнитного поля указано точками
Если начальная скорость частицы параллельна вектору магнитной индукции, то сила Лоренца равна нулю. Частица будет продолжать двигаться в том же направлении прямолинейно и равномерно.
Наконец, в общем случае можно представить себе, что частица влетает в область однородного магнитного поля со скоростью v, составляющей угол q с направлением магнитного поля. Эту скорость можно разложить на компоненту две составляющих, одна из которых
направлена вдоль поля, а вторая
перпендикулярна полю. Соответственно, движение частицы является суммой двух движений: равномерного вдоль поля со скоростью 

Рис. 5.15. Движение заряженной частицы по спирали в однородном магнитном поле
Пример. В однородном магнитном поле с индукцией 2 Тл движется протон. Траектория его движения представляет собой винтовую линию с радиусом 10 см и шагом 60 см. Определить скорость и кинетическую энергию протона. Какую ускоряющую разность потенциалов U прошел протон перед тем, как влететь в магнитное поле?
Решение. Из уравнений (5.11) находим угол между скоростью протона и полем
Кинетическая энергия протона будет
Мы могли использовать нерелятивистскую формулу для энергии, так как скорость протона много меньше скорости света.
Если протон ускорялся электрическим полем, то при прохождении разности потенциалов U он приобрел энергию eU. Отсюда находим разность потенциалов
Джоуль — слишком большая энергия в мире элементарных частиц. Здесь используют внесистемную единицу — электронвольт (эВ).
Электрон-вольт (эВ) — это внесистемная единица энергии, численно равная энергии, которую приобретает электрон, пройдя ускоряющую разность потенциалов 1 В
Она удобна тем, что любая другая частица с зарядом по модулю равным заряду электрона, ускоренная разностью потенциалов в 3,66 МэВ, как в нашем примере, имеет кинетическую энергию 3,66 МэВ (мегаэлектронвольт).
🌟 Видео
Атомный радиус (видео 5) | Периодическая таблица| ХимияСкачать
Урок 278. Задачи на силу Лоренца - 1Скачать

Движение свободных электронов в металлахСкачать

Теория движения заряженных частиц в электрическом поле .Часть 1Скачать

Урок 279. Задачи на силу Лоренца - 2Скачать
Определение радиуса полета электрона в магнитном поле, после вылета с фотокатода (0155) - часть 2Скачать