Как найти площадь четырехугольника если даны вершины

Видео:Задача с канала PreMath — попробуй найти площадь четырехугольникаСкачать

Четырехугольник и вектор на плоскости

Каждый школьник понимает, что параллелограмм является специальным видом плоских четырехугольников. Эта фигура состоит из двух пар параллельных пересекающихся отрезков. Она обладает следующими важными свойствами:

• ее противоположные стороны и углы равны друг другу;
• сумма всех четырех углов составляет 360 градусов;
• если просуммировать лишь два смежных (прилежащих к одной стороне) угла, то получится значение 180 градусов;
• любая диагональ делит фигуру на две равные части (треугольники);
• пересечение диагоналей происходит в точке, которая является геометрическим и массовым центром параллелограмма;
• любая секущая, которая проходит через геометрический центр, делит фигуру на две равные по площади части.

Специальные типы

Исходя из определения параллелограмма, как четырехугольника с параллельными и равными по длине противоположными сторонами, можно привести несколько видов фигуры, которые обладают высокой симметрией по отношению к ряду элементарных операций. Это следующие геометрические типы:

1. Квадрат. Все четыре стороны его равны по длине между собой, а углы составляют 90 градусов. Он является фигурой с достаточно высокой симметрией, и его площадь вычисляется просто как квадрат длины любой его стороны.
2. Прямоугольник. Еще один вид параллелограмма, все углы которого являются прямыми. Его симметрия несколько ниже, чем у квадрата, поскольку длины сторон равны лишь попарно. Площадь фигуры можно вычислить, перемножив длины смежных сторон.
3. Ромб. Специальный геометрический тип параллелограмма, который характеризуется тем, что длины всех его сторон являются одинаковыми. Углы фигуры попарно равны и отличаются от 90 градусов (два тупых и два острых).

Направленные отрезки и операция умножения

Площадь параллелограмма через векторы рассчитать легко, если знать понятие направленного отрезка и уметь работать с соответствующими математическими операциями. Поскольку любая точка на плоскости может быть представлена в виде набора двух координат в декартовой прямоугольной системе, то для P и Q можно записать:

P (x1, y1); Q (x2, y2).

Где числа x1, y1, x2 и y2 являются соответствующими координатами для точек P и Q по осям абсцисс и ординат. Чтобы получить вектор PQ-, который будет направлен из P в точку Q, необходимо из координат Q попарно вычесть значения для P:

PQ- = Q — P = (x2-x1, y2-y1).

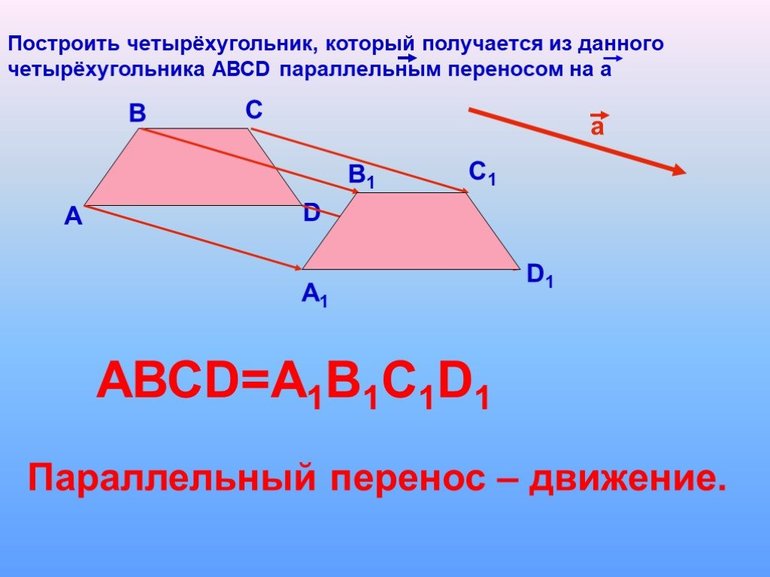
Координаты направленного отрезка на плоскости определяются так же, как и для точки, набором из двух чисел. Чтобы построить такой вектор в системе координат, необходимо его начало расположить в точке (0, 0), а конец со стрелкой будет располагаться в точке (x2-x1, y2-y1). Из этой геометрической интерпретации следует, что существует бесконечное множество направленных отрезков, которые эквивалентны между собой. Получаются они друг из друга с помощью параллельного переноса по всей плоскости координат.

Как и числа, направленные отрезки также можно складывать между собой, вычитать и умножать. Рассматривая вопрос построение параллелограмма на векторах и нахождения его площади, необходимо изучить свойства векторного произведения. Оно представляет собой вектор, перпендикулярный плоскости, в которой лежат исходные направленные отрезки. Пусть a- и b- необходимо умножить векторно. Результатом произведения будет следующий вектор c-:

c- = [a-*b-] = |a-|*|b-|*sin (alfa).

Здесь alfa — угол между a- и b-, а |a-| и |b-| — длины соответствующих направленных отрезков.

Направление c- принято определять с помощью правила правой руки. Оно гласит: если четыре пальца ладони направить от конца первого умножаемого вектора к концу второго, то оттопыренный большой палец укажет направление результирующего векторного умножения.

Координаты вектора c- можно вычислить также, если воспользоваться понятием определителя матрицы. Пусть a- имеет координаты (a1, a2), а b- = (b1, b2), тогда формула для определения c- запишется в следующем виде:

c- = (0, 0, (a1*b2-b1*a2)).

Вектор c- имеет первые две нулевые координаты, поскольку он перпендикулярен плоскости, в которой находятся a- и b-.

Видео:Вычисляем высоту через координаты вершин 1Скачать

Формула площади из геометрии

Чтобы получить формулу площади параллелограмма на векторах, необходимо вспомнить, как рассчитывается эта величина для треугольника. Если известна одна сторона (основание a) и высота, которая на нее опущена (h), то получается простое выражение:

Где S3 — площадь треугольника. Поскольку две таких плоских фигуры, которые соединены одной из своих сторон, образуют четырехугольник-паралелограм, то для него рассмотренную величину можно вычислить по формуле:

Пусть вторая сторона параллелограмма равна b, тогда с высотой h она связана через определение тригонометрической функции синус:

sin (alfa) = h/b => h = b*sin (alfa).

Если подставить это равенство в выражение для S4, то нахождение площади фигуры сведется к расчету произведения двух его смежных сторон и синуса угла между ними:

Поскольку угол alfa изменяется от 0 до 180 градусов, то функция синус всегда имеет положительное значение. Этой формулой часто пользуются на практике. Распространение инженерных калькуляторов позволяет быстро и с высокой точностью вычислять синусы любых углов.

Построение параллелограмма

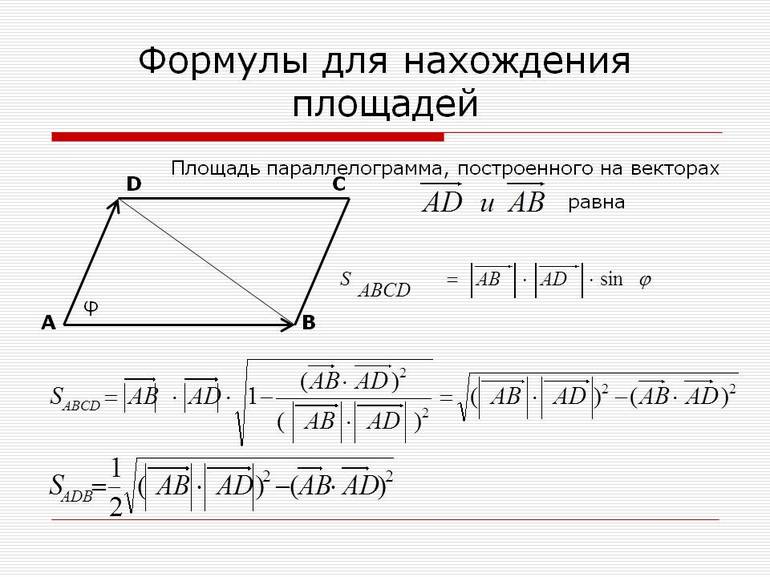
Определить площадь четырехугольника с попарно параллельными сторонами можно не только через длины его сторон. Если внимательно посмотреть на формулу для S4, то можно заметить, что она идентична по виду векторному произведению направленных отрезков.

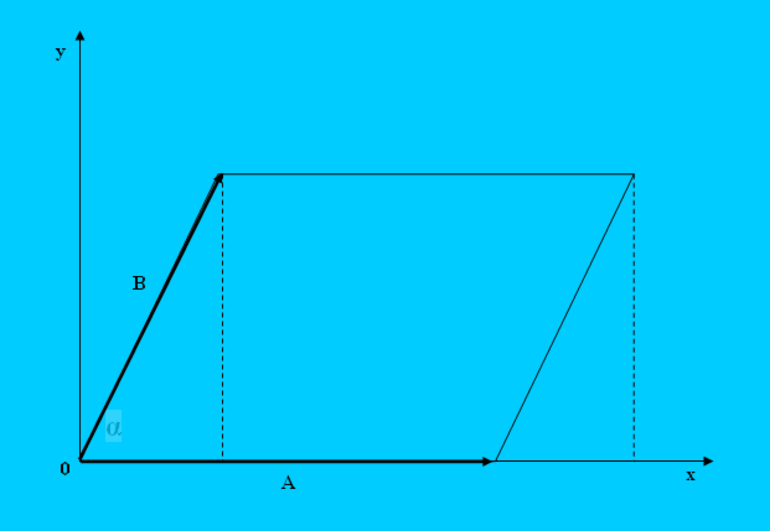
Пусть имеется два вектора a- и b-. Угол между ними равен alfa. Если их начала совместить в одной точке на плоскости, затем, от конца a- продолжить вектор b-, а из b- начертить a-, то получится параллелограмм, побудованый на a- и b-. Очевидно, что модуль векторного произведения этих направленных отрезков будет равен площади полученной фигуры:

S4 = a*b*sin (alfa) = |[a-*b-]|.

Применяя координатное выражение этого произведения, можно записать следующую формулу для площади:

Где a- = (a1,a2) и b-=(b1,b2). Знак модуля необходим потому, что по правилу правой руки могут получаться отрицательные векторы. Площадь же является всегда величиной положительной.

Преимущество последней записанной формулы для S4 по сравнению с выражением, где необходимо знать длины и углы, заключается в том, что ее использование не требует никаких предварительных вычислений. Достаточно лишь знать координаты конца и начала образующих параллелограмм векторов.

Задача с тремя точками

Чтобы научиться пользоваться записанной простой формулой, следует решить простую задачу. Имеется три точки, координаты которых следующие:

На вершинах этих точек следует построить параллелограмм, а затем, рассчитать его площадь S4.

Задачу проще всего решать через использование векторов. Выберем произвольную точку из трех заданных. Пусть это будет A. Из нее выходит два вектора: AB- и AC-. Их координаты определяются таким образом:

AB- = (2−1, 0-(-1)) = (1, 1); AC- = (-4−1, 3- (-1)) = (-5, 4).

Чтобы определить площадь параллелограмма на этих векторах, следует применить формулу для их векторного произведения. Порядок умножения направленных отрезков не имеет значения. Получается следующий результат:

S4 = [AB-*AC-] = 1*4 — (-5)*1 = 9.

Результат получен в единицах квадратных соответствующей двумерной системы координат.

Если была выбрана в качестве исходной не точка A, а B или C, то получился бы тот же результат, что можно доказать, проделав аналогичные вычисления.

Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Диагонали фигуры

Некоторые задачи по геометрии параллелограммов в качестве начального условия предлагают знание одной или двух его диагоналей. По этим данным необходимо вычислить характеристики всей фигуры, включая ее площадь. Решать такие задачи также удобно с использованием понятия векторов.

Если дана диагональ, выраженная вектором f- и основание, представленное направленным отрезком a-, то формула для площади параллелограмма имеет вид:

Где beta — угол между a- и f-. Видно, что это выражение не отличается от предыдущих для S4. Доказать его справедливость несложно, если рассмотреть построенные на указанных векторах треугольники и использовать признаки их подобия.

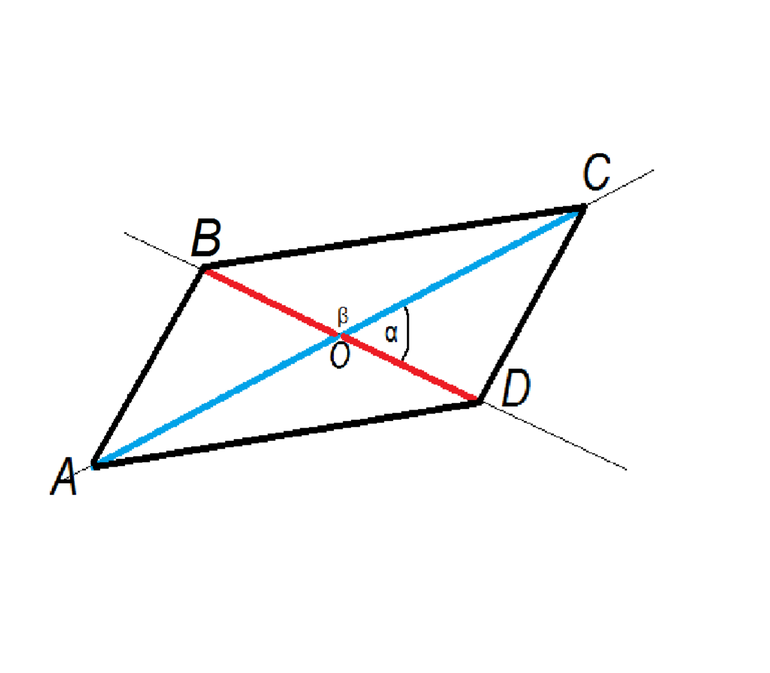
Другой случай, когда даны обе диагонали параллелограмма f- и e-. Воспользовавшись геометрическими построениями на плоскать, можно показать справедливость следующего выражения:

Здесь teta — это угол пересечения e- и f-. Таким образом, чтобы вычислить площадь параллелограмма, диагоналями которого служат вектора, следует вычислить половину модуля их векторного произведения.

Видео:№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

Пример решения

Все разнообразие задач на определение площади параллелограмма сводится к знанию единственной формулы векторного произведения. Пусть известны две диагонали фигуры. Они имеют координаты:

Чтобы определить величину S4, достаточно без промежуточных вычислений воспользоваться формулой векторного произведения заданных направленных отрезков:

В связи с развитием интернета, всегда можно использовать калькулятор-онлайн для расчета величины S4. Соответствующий электронный ресурс можно знайти, воспользовавшись любой поисковой системой в браузере.

Видео:Как найти площадь треугольника, зная координаты его вершины.Скачать

Трехмерное пространство

В пространственной системе координат каждый вектор задается тремя числами, поэтому их векторное произведение c- также будет представлять набор трех цифр. Построенный в пространстве параллелограмм на двух векторах будет иметь площадь, равную длине направленного отрезка c-. Для расчета его модуля следует использовать известное выражение: сумма квадратов трех координат под корнем.

Таким образом, площадь параллелограмма проще всего вычислять, используя операцию умножения векторов. Этот метод является универсальным не только для задач на плоскости, но и для решения проблем в трехмерной системе координат.

Видео:Вычисляем угол через координаты вершинСкачать

Решение. Задание 3, Вариант 2

Найти площадь четырехугольника ABCD, если его вершины имеют координаты A(1;1),B(-3;2),C(3;1)и D(2;-2).

Проще всего найти площадь ABCD как сумму площадей треугольников ABC и ACD. Основание этих треугольников AC=2, а высоты соответственно 1 и 3. Площадь ABCD равна 1+3=4.

Проверьте, что вы соединили вершины четырехугольника по порядку: ABCD.

Видео:Сможешь найти площадь четырехугольника? Его вершины лежат на окружностиСкачать

Это полезно

В нашей статье вы найдете всю необходимую теорию для решения задания №9 ЕГЭ по теме «Графики функций». Это задание появилось в 2022 году в вариантах ЕГЭ Профильного уровня.

Наш онлайн-курс по Физике

Все темы ЕГЭ с нуля

Можно не только читать, но и смотреть новые объяснения и разборы на нашем YouTube канале!

Пожалуйста, подпишитесь на канал и нажмите колокольчик, чтобы не пропустить новые видео

Задавайте свои вопросы в комментариях и оставляйте задачи, которые вы хотите, чтобы мы разобрали.

Мы обязательно ответим!

Мы заметили, что Вы регулярно пользуетесь нашими материалами для подготовки по физике.

Результат будет выше, если готовиться по отработанной методике.

У нас есть онлайн-курсы как для абитуриентов, так и для преподавателей.

Видео:ПЛОЩАДЬ ЧЕТЫРЕХУГОЛЬНИКА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Задачи на координатной сетке

Видео:Геометрия Как найти площадь четырехугольника, если нет формулыСкачать

Задачи на координатной сетке

Площадь фигур на координатной сетке или плоскости можно решить несколькими способами:

1. Достроить фигуру до прямоугольника или квадрата.

2. Найти площадь прямоугольника.

3. Найти площади всех дополнительных фигур (чаще всего это прямоугольные треугольники или трапеции).

4. Из площади прямоугольника вычесть все площади дополнительных фигур.

Найдите площадь четырёхугольника, вершины которого имеют координаты $(0;5), (4;7), (7;0), (11;2)$.

1. Достроим параллелограмм до прямоугольника

2. Найдем длину и ширину прямоугольника:

Чтобы найти длину стороны, параллельную какой либо оси, надо из большей координаты отнять меньшую координату.

Длина стороны $EF= 11$, стороны $FK= 7$. Подставим в формулу площади данные и сделаем вычисления: $S_= 11·7=77$.

3. Найдем площади дополнительных (ненужных) фигур:

4. Из площади прямоугольника вычтем все площади дополнительных фигур и таким образом получим площадь искомого параллелограмма.

• Второй способ

1. Если линии фигуры идут ровно по клеточкам и можно посчитать длины сторон, высот и т.д., то считаем клеточки и определяем величины.

2. Подставляем известные значения в формулу площади.

• Третий способ.

Площадь искомой фигуры можно найти по формуле Пика:

$S=/+В-1$, где $Г$ — количество узлов на границе фигуры (на сторонах и вершинах);

$В$ — количество узлов внутри фигуры.

Узел – это уголок клетки или пересечение линий

Найдите площадь четырёхугольника, изображённого на клетчатой бумаге с размером клетки $1 см × 1$ см. Ответ дайте в квадратных сантиметрах.

Отметим красными точками узлы на границе фигуры (Г), а желтыми – узлы внутри фигуры (В).

Подставим данные в формулу Пика: $S=/+6-1=3.5+6-1=8.5$

Площади некоторых фигур

Площадь треугольника:

1. $S=/$, где $h_a$ — высота, проведенная к стороне $а$
2. Для прямоугольного треугольника $S=/$, где $а$ и $b$ — катеты прямоугольного треугольника.
3. Для равностороннего треугольника $S=<a^√3>/$, где $а$ — длина стороны.

Площади четырехугольников:

1. Прямоугольник $S=a·b$, где $а$ и $b$ — смежные стороны.
2. Ромб $S=/$, где $d_1$ и $d_2$ — диагонали ромба
3. Трапеция $S=/$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
4. Квадрат $S=a^2$, где $а$ — сторона квадрата.
5. Параллелограмм $S=a·h_a$, где $h_a$ — высота, проведенная к стороне $а$.

Площадь круга:

$S=π·R^2$, где $π=3.14, R$ — радиус окружности.

Площадь сектора:

$S=<S_n°>/=/$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

Площадь кольца:

В прямоугольнике и квадрате центр описанной окружности лежит в точке пересечения диагоналей, а радиус описанной окружности равен половине диагонали.

В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы и радиус равен половине гипотенузы.

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

В прямоугольном треугольнике $АВС$, с прямым углом $С$

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

В прямоугольном треугольнике $АВС$ для острого угла $В$:

Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

$cos BOA= — cos BOC$;

$ctg BOA= — ctg BOC$.

Углы в окружности.

1. Угол, образованный двумя радиусами, называется центральным. Центральный угол равен градусной мере дуги, на которую он опирается.

2. Угол, вершина которого лежит на окружности, а стороны являются хордами, называется вписанным. Вписанный угол равен половине градусной меры дуги, на которую он опирается

Найдите величину угла MPK. Ответ дайте в градусах.

Угол $МРК$ равен половине градусной меры дуги $МК$, так как он вписанный. Чтобы отыскать градусную меру дуги, посмотрим, на сколько таких дуг мы можем разделить всю окружность, потом $360°$ разделим на полученное количество.

Дуга $МК$ отсекается хордой, занимающей две клетки. Разделим такими хордами всю окружность, получилось $8$ дуг.

$360:8=45°$, составляет градусная мера дуги $МК$.

Прямые на координатной плоскости

Координаты середины отрезка равны среднему арифметическому координат его концов.

Найдите абсциссу середины отрезка, соединяющего точки $В(2;8)$ и $A(6;4)$.

Пусть точка $М$ – середина отрезка $ВА$. Чтобы найти абсциссу данной точки, надо найти среднее арифметическое абсцисс концов отрезка:

Уравнение прямой, проходящей через две заданные точки на плоскости имеет вид $y=kx+b$, где $k$ и $b$ – это коэффициенты.

Уравнение можно задать с помощью формулы:

Точки пересечения прямой с осями координат:

Если прямая пересекает ось Ох, то в уравнении прямой координата $у = 0$, а если прямая пересекает ось Оу, то уравнении прямой координата $х = 0$.

Две прямые на координатной плоскости будут параллельны, если в уравнениях прямых будут равны коэффициенты k.

Если уравнение первой прямой: $y=k_x+b_1$;

Уравнение второй прямой: $y= k_x+b_2$, то при параллельности прямых, $k_1=k_2$.

🎥 Видео

Высшая математика. 3 урок. Аналитическая геометрия. Вычисление площади треугольникаСкачать

Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать

Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

Площадь четырёхугольника через диагоналиСкачать

ЕГЭ. Математика. База . Дан координаты вершин треугольника, найти площадь треугольникаСкачать

КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

Найдите площадь треугольника изображенного на клетчатой бумаге с размером клетки 1х1 см.Скачать

Вирусная задача. Найти площадь четырёхугольника.Скачать

№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

ОГЭ по математике. Площадь четырехугольника можно вычислить по формуле (вар. 5)Скачать

Найдите площадь четырёхугольникаСкачать