1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
| A ( ; ), B ( ; ), C ( ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. Содержание
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать  Определение принадлежности точки треугольникуДано: у нас есть треугольник, нам известны только координаты его вершин. У нас есть точка, нам известны её координаты. Что нужно узнать: нужно установить принадлежность точки треугольнику. В данной статье разбирается несколько разных методов определения принадлежности точки треугольнику. Видео:Как найти площадь треугольника? #треугольник #математика #егэ #shorts #подготовкакегэ #огэ #площадьСкачать  Метод сравнения площадейВ данном методе сначала находятся площади 3-х треугольников, которые образует данная точка с каждой стороной треугольника. В нашем случае(рис. 1) это треугольники ABP, BCP, CAP и их площади s1, s2, s3 соответственно. Затем находится площадь самого треугольника ABC. Найденный площади сравниваются — если сумма 3-х площадей равна площади всего треугольника, то значит точка принадлежит треугольнику. При сравнении, как правило, задаётся погрешность. Так как у нас известны только координаты точек, то все площади, находятся по формуле Герона, от обильности операций которой становится ясно, почему этот метод очень трудоёмкий. Простейшая реализация алгоритма: Атрибуты функции: aAx, aAy, aBx, aBy, aCx, aCy — координаты точек A, B, C треугольника; aPx, aPy — координаты точки, принадлежность которой надо определить. Видео:Как найти площадь треугольника без формулы?Скачать  Метод относительностиДанный метод заключается в следующем. Сначала выбирается ориентация движения по вершинам треугольника(по часовой или против часовой стрелке). Я выбираю по часовой. На рисунке 2 выбранная ориентация движения(по часовой) показана стрелками. По данной ориентации проходим все стороны треугольника, рассматривая их как прямые, и рассчитываем по какую сторону от текущей прямой лежит наша точка. Не трудно догадаться, что если точка для всех прямых, при нашей ориентации, лежит с правой стороны, то значит точка принадлежит треугольнику, а если хоть для какой-то прямой она лежит с левой стороны, то значит условие принадлежности не выполняется. На рисунке 2 продемонстрирована ситуация, когда точка только для одной прямой AB лежит по левую сторону, а значит не принадлежит треугольнику. Видео:Площадь прямоугольного треугольника. Как найти площадь прямоугольного треугольника?Скачать  Всё относительно!Тут надо кое что пояснить, весьма не маловажное, что может сыграть роль в оптимизации и выборе алгоритма. Обратите внимание, что в приведённом коде есть закомментированные блоки кода с комментариями «для строгой ориентации», в то время как рабочий код универсален — он предназначен для любой ориентации. Т.е. представленный код определит принадлежность точки для любого заданного треугольника. В моей тестирующей программе треугольники как раз таки строятся по random()-у координат вершин, а ориентация идёт по вершинам(A>B>C>A). Для рисунка 2 — это по часовой стрелки, но для рисунка 3 — это против часовой. Так вот, в случае рисунка 3 точка должна лежать по левую сторону векторов, чтобы принадлежать треугольнику. Вот тут и получается важный момент! Если вы уверены, что в вашем проекте все треугольники будут ориентированы по часовой стрелке(а т.е. вершина C будет всегда правее вектора AB), то вам можно закомментировать блок универсального решения и раскомментировать блок «для строгой ориентации по часовой» и данный алгоритм упрощается аж на 3 логических операции! Видео:8 класс, 14 урок, Площадь треугольникаСкачать  Векторный методТретий метод который я освещаю для меня самый интересный. Идея его применения зарождается если взглянуть на треугольник как на половинку параллелограмма… Данный метод я сначала проверил на бумаге. После всех оптимизаций формул, как всё сошлось, я реализовал его в коде, где он показал себя вполне успешным и результативным. Аж эффективнее 2-х предыдущих методов :] 1) одну вершину треугольника помещаем в координаты (0;0); 2) две стороны, выходящие из этой вершины, представляем как вектора. Таким образом из всего этого появляется система простых условий нахождения точки P между векторами b и c.(рис. 4)
Видео:Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать  Все формулы для треугольникаВидео:КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать  1. Как найти неизвестную сторону треугольникаВычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу. a , b , c — стороны произвольного треугольника α , β , γ — противоположные углы Формула длины через две стороны и угол (по теореме косинусов), ( a ): * Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение Формула длины через сторону и два угла (по теореме синусов), ( a): Видео:Нахождение площади равнобедренного треугольника при помощи теоремы Пифагора | Геометрия | АлгебраСкачать  2. Как узнать сторону прямоугольного треугольникаЕсть следующие формулы для определения катета или гипотенузы a , b — катеты c — гипотенуза α , β — острые углы Формулы для катета, ( a ): Формулы для катета, ( b ): Формулы для гипотенузы, ( c ): Формулы сторон по теореме Пифагора, ( a , b ): Видео:Периметр треугольника. Как найти периметр треугольника?Скачать  3. Формулы сторон равнобедренного треугольникаВычислить длину неизвестной стороны через любые стороны и углы b — сторона (основание) a — равные стороны α — углы при основании β — угол образованный равными сторонами Формулы длины стороны (основания), (b ): Формулы длины равных сторон , (a): Видео:Площади фигур. Сохраняй и запоминай!#shortsСкачать  4. Найти длину высоты треугольникаВысота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом). Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.
a — сторона, основание b, c — стороны β , γ — углы при основании p — полупериметр, p=(a+b+c)/2 R — радиус описанной окружности S — площадь треугольника Формула длины высоты через стороны, ( H ): Формула длины высоты через сторону и угол, ( H ): Формула длины высоты через сторону и площадь, ( H ): Формула длины высоты через стороны и радиус, ( H ): 📺 ВидеоКак найти площадь этого треугольника, не зная формулы?Скачать  Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать  Задача, которую исключили из экзамена в АмерикеСкачать  Как найти площадь треугольникаСкачать 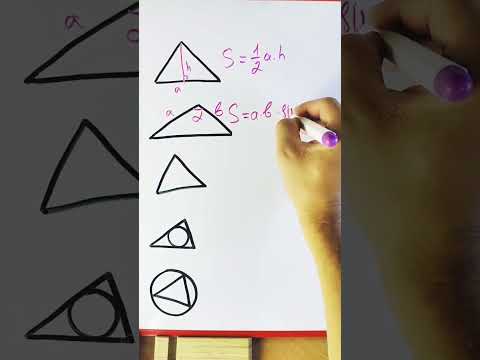 Формулы равностороннего треугольника #shortsСкачать  Найдите площадь треугольника изображенного на клетчатой бумаге с размером клетки 1х1 см.Скачать  Лайфхак! Площади всех фигур #огэ #математика #shortsСкачать  ВСЕ ВИДЫ ТРЕУГОЛЬНИКОВ😉 #егэ #огэ #математика #профильныйегэ #shorts #геометрия #образованиеСкачать  Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать  Задача найти площади треугольников при пересечении медианСкачать  | ||
 Рис. 4.
Рис. 4.















 H — высота треугольника
H — высота треугольника

