Как найти кривизну окружности

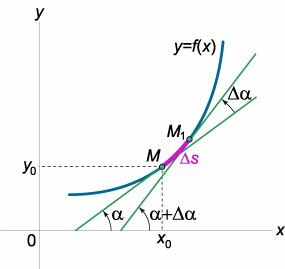
Рассмотрим плоскую кривую, заданную уравнением (y = fleft( x right).) Пусть в точке (Mleft( right)) проведена касательная к данной кривой, которая образует угол (alpha) с осью абсцисс (рисунок (1)). При смещении (Delta s) вдоль дуги кривой точка (M) переходит в точку (.) При этом положение касательной также изменяется: угол наклона касательной к оси (Ox) в точке () будет составлять (alpha + Deltaalpha.) Таким образом, при смещении точки кривой на расстояние (Delta s) касательная поворачивается на угол (Deltaalpha.) (Будем считать, что угол (alpha) возрастает при вращении против часовой стрелки.)

Абсолютное значение отношения (largefrac<><>normalsize) называется средней кривизной дуги (M.) В пределе, при (Delta s to 0,) мы получаем кривизну кривой в точке (M:) [K = limlimits_ left| <frac<><>> right|.] Из приведенного определения следует, что кривизна в какой-либо точке кривой характеризует скорость вращения касательной в этой точке.

Для плоской кривой (y = fleft( x right)) кривизна в точке (Mleft( right)) выражается через первую и вторую производные функции (fleft( x right)) по формуле [K = frac <<left| right|>> <<<<left[ <1 + <<left( right)>^2>> right]>^<largefracnormalsize>>>>.] Если кривая задана в параметрической форме уравнениями (x = xleft( t right),) (y = yleft( t right),) то ее кривизна в произвольной точке (Mleft( right)) равна [K = frac <<left| right|>> <<<<left[ <<<left( right)>^2> + <<left( right)>^2>> right]>^<largefracnormalsize>>>>.] В случае, если кривая задана полярным уравнением (r = rleft( theta right),) кривизна находится по формуле [K = frac <<left| <+ 2 <<left( right)>^2> — rr»> right|>> <<<<left[ <+ <<left( right)>^2>> right]>^<largefracnormalsize>>>>.] Радиусом кривизны кривой в точке (Mleft( right)) называется величина, обратная кривизне (K) данной кривой в рассматриваемой точке: [R = frac.] Следовательно, для плоских кривых, заданных явным уравнением (y = fleft( x right),) радиус кривизны в точке (Mleft( right)) будет определяться выражением [R = frac <<<<left[ <1 + <<left( right)>^2>> right]>^<largefracnormalsize>>>> <<left| right|>>.]

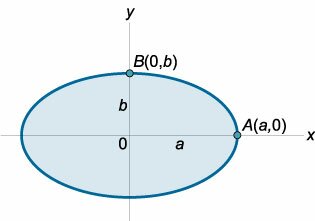
Очевидно, достаточно найти кривизну эллипса в точках (Aleft( right)) и (Bleft( right)) (рисунок (2)), поскольку в силу симметрии кривой кривизна в двух противоположных вершинах эллипса будет такой же.

Для расчета кривизны удобно перейти от канонического уравнения эллипса к уравнению в параметрической форме : [x = acos t,;;;y = bsin t.] где (t) − параметр. В точке (Aleft( right)) параметр имеет значение (t = 0,) а в точке (Bleft( right)) его значение равно (t = largefracnormalsize.)

Данная функция достигает максимума в точках (x = largefrac<>normalsize,;n in Z.) В силу периодичности кривизна во всех точках максимума одинакова, поэтому достаточно рассмотреть лишь точку (x = 0).

В данном случае точка (x = 0) является точкой перегиба функции (y = arctan x.) Поскольку в точке перегиба вторая производная равна нулю, то кривизна здесь также должна быть равна нулю, что и показывает полученное решение.

Экспоненциальная функция (y = ) − это единственная уникальная функция, у которой производные любого порядка равны самой функции. Поэтому для кривизны данной кривой можно сразу написать следующую формулу: [ <K = frac<<left| right|>> <<<<left[ <1 + <<left( right)>^2>> right]>^<largefracnormalsize>>>> > = <frac<<>><<<<left( <1 + <e^>> right)>^<largefracnormalsize>>>>.> ] Знак модуля в числителе опущен, поскольку экспоненциальная функция всегда положительна.

Радиус кривизны плоской кривой

Любая линия является кривой, даже прямая. Поэтому к любой линии применимы такие характеристики как кривизна или радиус кривизны. Как правило кривизна обозначается латинской литерой k, а радиус кривизны греческой литерой ρ.

Между собой эти характеристики кривой связаны следующим образом:

k = 1/ρ (542.1)

Т.е. чем больше радиус кривой, тем меньше ее кривизна.

А теперь рассмотрим несколько частных случаев кривых.

Радиус кривизны окружности

Окружность — это плоская кривая с постоянным радиусом кривизны. Т.е. радиус окружности это и есть радиус кривизны окружности:

Как определить радиус окружности, мы рассмотрим ниже.

Кривизна дуги

Любая дуга — это часть окружности. Соответственно радиус дуги равен радиусу окружности:

Рисунок 542.1. Дуга — часть окружности

На рисунке 542.1 мы видим дугу АВ, показанную оранжевым цветом, являющуюся частью окружности с радиусом R. Кроме того, мы видим, что угол α, образованный радиусами в точках А и В, равен углу между касательными (показаны фиолетовым цветом) к окружности в этих точках.

Эти закономерности позволяют определить радиус дуги и найти центр окружности даже тогда, когда изначально мы окружность не видим, а только имеем дугу.

Понятие кривизны дуги формулируется так:

Кривизна дуги — это отношение угла между касательными, проведенными в начале и конце дуги, к длине дуги

Т.е. зная длину дуги m и угол α между касательными, мы можем определить кривизну дуги:

А так как длина дуги зависит от угла между радиусами или между касательными в концах дуги:

то, подставив значение длины дуги в уравнение (542.3), получим:

Примечание: При измерении угла между касательными не в радианах, а в градусах уравнение длины дуги имеет другой вид:

но сути дела это не меняет. Такая запись по-прежнему означает, что мы рассматриваем часть длины окружности. Так при α = 360° дуга становится окружностью

Более того, сама идея радианов на этой формуле и основана, так прямой угол 90° = П/2, развернутый 180° = П и т.д.

И еще одно интересное свойство дуги: Если соединить точки А и В прямой линией, то угол между этой линией и касательными будет равен α/2, а сама прямая линия — это и есть расстояние между точками А и В. Если дуга расположена в плоскости соответствующим образом, например так, как показано на рисунке 542.2:

Рисунок 542.2. Дуга из точки начала координат.

то расстояние между точками — это проекция l дуги на ось х. А максимальное расстояние между дугой и осью х — это стрела дуги h.

Радиус кривизны прямой линии

Любая прямая линия, даже бесконечно длинная, может рассматриваться как бесконечно малая часть окружности, т.е. как дуга. Соответственно в каких единицах измерять радиус такой окружности даже трудно представить.

Поэтому обычно прямой линией называют кривую с бесконечно большим радиусом:

k_п.л = 1/∞ = 0 (542.6)

Про до сих пор неразрешенный парадокс, возникающий при подобных подходах к прямой линии и к окружности, я уже упоминал в статье «Основы геометрии. Определения основных элементов, пятый элемент». Здесь лишь добавлю, что через прямую линию можно провести бесконечное множество плоскостей и в любой из этих плоскостей радиус кривизны прямой линии будет равен бесконечности. При этом через окружность можно провести две взаимно перпендикулярные плоскости, в одной из которых окружность будет окружностью, а в другой — прямой линией конечной длины. Поэтому

все линии, которые в одной из плоскостей имеют бесконечно большой радиус кривизны, считаются плоскими

Ну и на закуску еще несколько парадоксов, на этот раз связанных с определениями кривизны и радиуса:

1. Из уравнения (542.1) можно сделать вывод, что:

kp = 1 (542.7)

Соответственно для прямой линии:

0·∞ = 1 (542.7.2)

Т.е. если бесконечно много раз взять ноль, то на единичку мы наскребем. Впрочем дальше будет еще веселее.

2. Если прямая — это дуга с бесконечно большим радиусом, соответственно касательные, проведенные в концах такой дуги, совпадают с прямой, а угол, образованный касательными, равен нулю.

Это означает, что радиусы проведенные в концах дуги — прямой линии, являются параллельными прямыми и не могут пересекаться. А между тем по определению это радиусы, которые обязательно должны сходиться в некоторой точке — центре окружности.

Получается, что параллельные прямые пересекаться не должны, но где-то в бесконечности все-таки пересекаются.

Разрешить этот парадокс пытались многие математики, однако в пределах евклидовой геометрии при принятом толковании определений данный парадокс не разрешим.

Радиус кривизны точки

Точка — это самый простой и самый сложный элемент геометрии. Одни считают, что точка не имеет размеров, а значит и определить кривизну или радиус кривизны точки не возможно. Другие, в частности Евклид, считают, что точка не имеет частей, а каковы при этом размеры точки — не совсем понятно. Я же считаю, что точка — это начальный, далее не делимый элемент геометрии, размеры которого пренебрежимо малы по сравнению с остальными рассматриваемыми элементами. В этом случае для точки будут справедливыми следующие уравнения кривизны и радиуса кривизны:

k_т. = 1/0 = ∞ (542.9)

И хотя нас с первых лет обучения в школе учат, что делить на 0 нельзя и даже встроенный в операционную систему калькулятор пишет, что «деление на ноль невозможно», тем не менее делить на ноль можно, а результатом деления всегда будет бесконечность.

Как и в случае с прямой мы имеем парадоксальный результат, выражаемый формулой (542.5.2). Тем не менее точку также можно отнести к плоской кривой, имеющей постоянный радиус кривизны.

Примечание: На мой взгляд большинство из описанных выше парадоксов возникают из-за неправильного толкования понятия «бесконечность». Бесконечность как некая абсолютная величина не имеет пределов, а значит и никакому измерению не поддается. Кроме того бесконечность — это даже не постоянная, а переменная величина. Например луч — это прямая линия с началом в некоторой точке. Длина луча может быть бесконечно большой. При этом прямая линия тоже может быть бесконечно длинной при этом не иметь ни начала ни конца. Получается, что с одной стороны бесконечно длинный луч вроде бы в 2 раза короче, чем бесконечно длинная прямая. А с другой стороны длины их бесконечны и поэтому равны.

Возможным выходом из этой ситуации является принятие понятия «бесконечность», как относительного. Например, кривизна прямой линии является пренебрежимо малой величиной по отношению к радиусу кривизны. Или радиус кривизны прямой линии несопоставимо больше кривизны. Подобные толкования допускают и наличие кривизны прямой и некое конечное значение радиуса кривизны прямой и многое другое. Я бы назвал такой относительный подход к рассмотрению проблемы реалистичным, а подходы, использующие абсолютные понятия — идеализированными. Впрочем прямого отношения к теме данной статьи это не имеет. Продолжим рассмотрение плоских кривых.

И окружность и прямая линия являются плоскими кривыми с постоянным радиусом кривизны. При этом радиус кривизны прямой линии всегда известен, так как равен бесконечности, а для окружности всегда можно определить радиус, воспользовавшись теоремой Пифагора. Так в частном случае, если центр окружности совпадает с началом координат рассматриваемой плоскости (u = 0; v = 0 — координаты центра окружности), то:

Рисунок 541.4. Радиус окружности, как гипотенуза прямоугольного треугольника.

R 2 = x 2 + y 2 (541.1.2)

А в общем случае, когда координаты центра окружности не совпадают с началом координат:

Рисунок 542.3. Окружность, центр которой не совпадает с началом координат.

R 2 = (x — u) 2 + (y — v) 2 (542.10)

Но в жизни достаточно часто приходится сталкиваться с кривыми, радиус кривизны которых — не постоянная величина. Более того, этот радиус может изменяться в двух плоскостях измерения. Тем не менее так далеко углубляться в геометрию и алгебру мы не будем и далее рассмотрим, как можно определить радиус плоской кривой в некоторой точке.

Плоские кривые с изменяющимся радиусом кривизны

Примеров плоских кривых с изменяющимся радиусом кривизны очень много, это и гиперболы, и параболы, и синусоиды и т.п. Определение радиуса кривизны таких кривых основано на следующих теоретических предпосылках:

1. Любую окружность можно рассматривать как некоторое множество дуг.

2. Если количество дуг, составляющих окружность, стремится к бесконечности, то соответственно длина таких дуг стремится к нулю (m → 0).

3. Если мы обозначим длину такой очень короткой дуги как приращение функции длины окружности (m = Δl), то уравнение кривизны (542.3) примет следующий вид:

(542.3.1)

4. Тогда любую плоскую кривую с изменяющимся радиусом можно рассматривать как стремящееся к бесконечности множество дуг с постоянным радиусом. Другими словами в пределах любой кривой, описываемой параметрическими уравнениями, всегда можно выделить дугу, пусть даже и очень малой длины, стремящейся к точке и определить для нее кривизну и радиус кривизны в рассматриваемой точке.

Это означает, что самый точный способ определения радиуса кривизны в таком случае — это использование дифференциальных исчислений. В общем случае для этого нужно два раза продифференцировать уравнение радиуса окружности (542.10) по аргументу функции х, а затем извлечь квадратный корень из полученного результата. В итоге (полный вывод уравнения здесь не привожу из-за повышенной сложности записи, а для особо заинтересованных есть справочники и другие сайты) мы получим следующую формулу для определения радиуса кривизны:

(542.11)

Соответственно кривизна плоской кривой в рассматриваемой точке будет равна:

(542.12)

В частном случае, когда тангенс угла между касательными — первая производная от функции — является относительно малой величиной, например, tg2° = 0.035 соответственно (tg2°) 2 = 0.0012, то влиянием куба суммы первой производной и единицы на кривизну можно пренебречь (значение знаменателя дроби сводится к единице) и тогда:

k = y» = d 2 y/dx 2 (542.12.2)

Т.е. формально в таких случаях кривизной считается не отношение угла наклона между касательными к длине дуги, а некоторая величина, примерно соответствующая высоте h на рисунке 542.2.

Эта особенность второй производной очень активно используется в частности для упрощения определения прогиба элементов строительных конструкций.

На этом пока все.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630

Категории:

• Расчет конструкций . Основы прикладной геометрии

Оценка пользователей:10.0 (голосов: 1)Переходов на сайт:6701Комментарии:

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Радиус, круг и центр кривизны

Вы будете перенаправлены на Автор24

Смысл понятий радиуса, круга и центра кривизны

В технических приложениях часто оказывается удобным использовать окружности для приближенной замены кривой в окрестностях рассматриваемых точек. Это существенно упрощает решение целого ряда задач за счет применения более удобных выражений.

Наиболее употребительными характеристиками любой кривой являются касательная и нормаль. Касательная — предельное положение секущей $MN$ при неограниченном приближении точки $N$ к точке $M$ вдоль кривой. Нормаль — прямая, проходящая через точку касания перпендикулярно касательной.

Уравнение касательной в точке $Mleft(x_ ,y_ right)$ к кривой $y=fleft(xright)$ имет вид $y-y_ =y’left(x_ right)cdot left(x-x_ right)$, уравнение нормали $y-y_ =-frac <y'left(x_right)> cdot left(x-x_ right)$.

Записать уравнения касательной и нормали к кривой $y=3cdot x^ -x+2$ в заданной точке $x_ =1$.

Значение функции в заданной точке: $y_ =yleft(x_ right)=yleft(1right)=3cdot 1^ -1+2=4$.

Значение производной в заданной точке:

[y’=left(3cdot x^ -x+2right)^ <> =6cdot x-1; y’left(x_ right)=y’left(1right)=6cdot 1-1=5.]

Уравнение касательной: $y-4=5cdot left(x-1right)$ или $5cdot x-y-1=0$.

Уравнение нормали: $y-4=-frac cdot left(x-1right)$ или $x+5cdot y-21=0$.

Радиус кривизны — это параметр кривой, значение которого обратно значению кривизны $R=frac $. Следовательно, это такая же переменная величина, как и кривизна.

Если в данной точке $M$ построить нормаль к кривой и отложить на ней в сторону вогнутости кривой отрезок, равный по длине радиусу кривизны кривой в этой точке, то получим точку — центр кривизны. Окружность с центром в полученной точке и радиусом, равным радиусу кривизны — это круг кривизны. Так как данная кривая и её круг кривизны касаются в данной точке, то они имеют в данной точке общую касательную. Кроме того, значения кривизны кривой и круга кривизны в данной точке совпадают.

Важным свойством круга кривизны является то, что он является соприкасающимся кругом, то есть предельным положением круга, проходящего через три точки кривой, стремящимся к совпадению в данной.

Если некоторая точка перемещается вдоль кривой, то и соответствующий ей центр кривизны также описывает некоторую кривую. Геометрическое место центров кривизны данной кривой называется её эволютой. При этом данная кривая по отношению к своей эволюте называется её эвольвентой.

Вычисление радиуса и определение центра круга кривизны

Формулы для радиуса кривизны получить легко, если известны формулы для вычисления кривизны кривой.

При произвольном параметрическом задании кривой $x=xleft(tright)$ и $y=yleft(tright)$ имеем $R=frac <sqrt<left(left(x'_right)^ +left(y’_ right)^ right)^ > > <y''_cdot x'_ -x''_ cdot y'_ > $.

Если кривая задана в явном виде $y=fleft(xright)$, то $R=frac <sqrt<left(1+left(y'right)^right)^ > > $.

Если кривая задана в полярных координатах $rho =rho left(phi right)$, то $R=frac <sqrt<left(rho ^+left(rho '_ right)^ right)^ > > <rho ^+2cdot left(rho '_ right)^ -rho cdot rho ''_ > $.

Готовые работы на аналогичную тему

Найти радиус кривизны экспоненты $y=e^ $ при $x=0$.

Находим производные: $y'=e^ $; $y''=e^ $.

По формуле для радиуса кривизны получаем:

Вычисляем радиус кривизны экспоненты при $x=0$:

Найти радиус кривизны кардиоиды $rho =1+cos phi $.

Находим производные: $rho '=-sin phi $; $rho ''=-cos phi $.

[rho ^ +rho '^ =left(1+cos phi right)^ +left(-sin phi right)^ =2cdot left(1+cos phi right);] [rho ^ +2cdot rho '^ -rho cdot rho ''=left(1+cos phi right)^ +2cdot left(-sin phi right)^ -left(1+cos phi right)cdot left(-cos phi right)=] [=3cdot left(1+cos phi right).]

По формуле для радиуса кривизны получаем:

Найдем координаты центра кривизны $Pleft(x_ ;y_ right)$ кривой $y=fleft(xright)$.

Координаты центра кривизны для точки $Mleft(x;yright)$ удовлетворяют уравнению нормали $y_ -y=-frac cdot left(x_ -xright)$.

Уравнение круга кривизны: $left(x-x_ right)^ +left(y-y_ right)^ =R^ $.

Координаты центра кривизны по существу являются параметрическими уравнения эволюты.

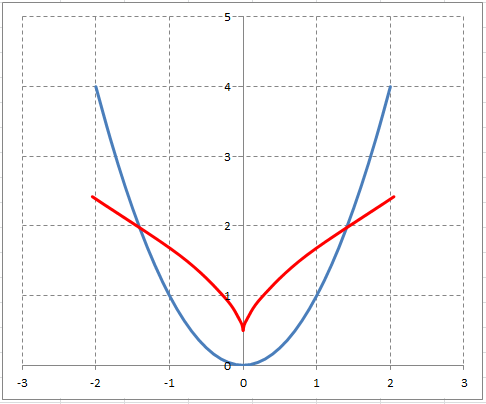
Найти эволюту параболы $y=x^ $. Результаты представить графически.

Находим производные: $y'=2cdot x$; $y''=2$.

По формулам $left<begin <x_=x-frac <y'cdot left(1+y'^right)> > \ <y_=y+frac <1+y'^> > endright. $ находим координаты центра кривизны для произвольной точки $Mleft(x;yright)$.

Полученные выражения фактически представляют собой параметрические уравнения эволюты, в которых $x$ является параметром. Если исключить параметр $x$ из этих уравнений, то может быть получено уравнение вида $Fleft(x_ ;y_ right)=0$, которое непосредственно связывает координаты эволюты.

Совмещенный график эвольвенты $y=x^ $ и её эволюты:

На графике синей линией изображена парабола $y=x^ $, а красной линией -- её эволюта. Эволюта представляет собой полукубическую параболу.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 30 11 2022

💥 Видео