В треугольнике ABC стороны Первая окружность вписана в треугольник АВС, а вторая касается AB и продолжения сторон BC и AC.
а) Доказать, что отношение радиусов окружностей равно 2 : 1.
б) Найти расстояние между точками касания окружностей стороны AB, если АС = 15.
а) Пусть стороны треугольника
По обратной теореме Пифагора он прямоугольный, поэтому его площадь
полупериметр
По формулам для радиусов вписанной и вневписанной окружности находим
что и требовалось доказать.
б) По формуле для отрезков от вершины до точки касания с вписанной или вневписанной окружностью имеем:
Поскольку
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 |
| Получен обоснованный ответ в пункте б. Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 |
| Имеется верное доказательство утверждения пункта а. При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. Содержание
Видео:Сможешь найти расстояния между точками касания?Скачать  Расстояния между двумя точкамиНа данной странице калькулятор поможет рассчитать расстояние между двумя точками онлайн в плоскости и пространстве. Для расчета задайте координаты.
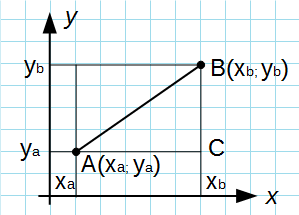
Расстояния между двумя точкамиФормула вычисления расстояния между двумя точками A(xa; ya) и B(xb; yb) на плоскости: Формула вычисления расстояния между двумя точками A(xa; ya; za) и B(xb; yb; zb) в пространстве: Вывод формулы для вычисления расстояния между двумя точками на плоскостиИз точек A и B опустим перпендикуляры на оси координат x и y. Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны: Спомощью теоремы Пифагора, вычислим длину отрезка AB: Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости. Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично. Видео:№940. Найдите расстояние между точками А и В, если: а) А (2; 7), В (-2; 7); б) А (-5; 1), В (-5; -7)Скачать  Найдите расстояние между точками касания окружности сторон угла aВидео:Расстояние между точкамиСкачать  Разделы Видео:Расстояние между двумя точками. Координаты середины отрезка.Скачать  ДополнительноЗадача по математике — 4162Две окружности касаются друг друга внешним образом в точке $C$. Радиусы окружностей равны 2 и 7. Общая касательная к обеим окружностям, проведённая через точку $C$, пересекается с другой их общей касательной в точке $D$. Найдите расстояние от центра меньшей окружности до точки $D$. Задача по математике — 4163Теорема Брахмагупты. Диагонали вписанного четырёхугольника перпендикулярны и пересекаются в точке $P$. Докажите, что прямая, проходящая через точку $P$ и перпендикулярная одной из сторон четырёхугольника, делит противоположную сторону пополам. Задача по математике — 4164Две окружности касаются друг друга внешним образом в точке $A$. Найдите радиусы окружностей, если хорды, соединяющие точку $A$ с точками касания с одной из общих внешних касательных, равны 6 и 8. Задача по математике — 4165Найдите отношение радиусов двух окружностей, касающихся между собой, если каждая из них касается сторон угла, равного $alpha$. Задача по математике — 4166В острый угол, равный $60^$, вписаны две окружности, касающиеся друг друга внешним образом. Радиус меньшей окружности равен $r$. Найдите радиус большей окружности. Задача по математике — 4167В равнобедренной трапеции лежат две окружности. Одна из них, радиуса 1, вписана в трапецию, а вторая касается двух сторон трапеции и первой окружности. Расстояние от вершины угла, образованного двумя сторонами трапеции, касающимися второй окружности, до точки касания окружностей вдвое больше диаметра второй окружности. Найдите площадь трапеции. Задача по математике — 4168В параллелограмме лежат две окружности. Одна из них, радиуса 3, вписана в параллелограмм, а вторая касается двух сторон параллелограмма и первой окружности. Расстояние между точками касания, лежащими на одной стороне параллелограмма, равно 3. Найдите площадь параллелограмма. Задача по математике — 4169Дана окружность радиуса 1. Из внешней точки $M$ к ней проведены две взаимно перпендикулярные касательные $MA$ и $MB$. Между точками касания $A$ и $B$ на меньшей дуге $AB$ взята произвольная точка $C$ и через неё проведена третья касательная $KL$, образующая с касательными $MA$ и $MB$ треугольник $KLM$. Найдите периметр этого треугольника. Задача по математике — 4170Две окружности радиусов $R$ и $r$ касаются сторон данного угла и друг друга. Найдите радиус третьей окружности, касающейся сторон того же угла, и центр которой находится в точке касания двух данных окружностей между собой. Задача по математике — 4171В треугольник со сторонами 6, 10, и 12 вписана окружность. К окружности проведена касательная так, что она пересекает две большие стороны. Найдите периметр отсечённого треугольника. Задача по математике — 4172Сторона треугольника равна 48, а высота, проведённая к этой стороне, равна 8,5. Найдите расстояние от центра окружности, вписанной в этот треугольник, до вершины, противоположной данной стороне, если радиус вписанной окружности равен 4. Задача по математике — 4173В угол вписаны три окружности — малая, средняя и большая. Большая окружность проходит через центр средней, а средняя — через центр малой. Вычислите радиусы средней и большой окружности, если радиус малой равен $r$, и расстояние от её центра до вершины угла равно $a$. Задача по математике — 4174Три окружности радиусов 1, 2 и 3 касаются друг друга внешним образом. Найдите радиус окружности, проходящей через точки касания этих окружностей. Задача по математике — 4175В равносторонний треугольник со стороной $a$ вписана окружность. К окружности проведена касательная так, что её отрезок внутри треугольника равен $b$. Найдите площадь треугольника, отсечённого этой касательной. Задача по математике — 4176Три окружности разных радиусов попарно касаются друг друга внешним образом. Отрезки, соединяющие их центры, образуют прямоугольный треугольник. Найдите радиус меньшей окружности, если радиусы большей и средней равны 6 и 4. 🎬 ВидеоДосрочный ОГЭ (2 вариант). Задание 4.Скачать  Длина отрезкаСкачать  Всё про углы в окружности. Геометрия | МатематикаСкачать  №74. Точка N лежит на отрезке МР. Расстояние между точками М и Р равно 24 см, а расстояние междуСкачать 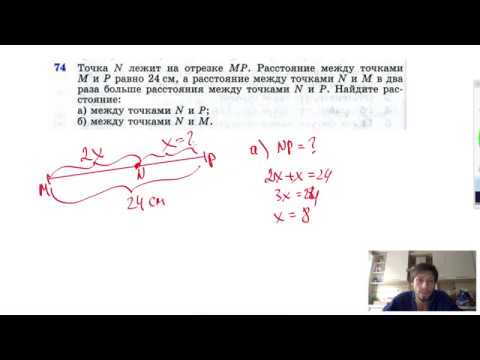 №946. Найдите х, если: а) расстояние между точками А (2; 3) и В (х; 1) равно 2Скачать  Расстояние между точками координатной прямой. Математика 6 классСкачать  Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  Задача №24. ОГЭ по математике. | Математика | TutorOnlineСкачать  Координаты середины отрезкаСкачать  Отрезки касательных из одной точки до точек касания окружности равны | Окружность | ГеометрияСкачать  На окружности с центром O отмечены точки A и B так ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать  Расстояние между точками. Геометрия 9 класс.Скачать  Уравнение окружности и формула расстояния между точками на плоскостиСкачать  4 класс, 40 урок, Расстояние между точками координатного лучаСкачать  ☀️СТЕРЕОМЕТРИЯ В ЕГЭ | НАЙТИ РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ, УГОЛ И ПРОЧЕЕ | ЗАДАНИЕ 5 ЕГЭ 2022 |Скачать  ОГЭ Задание 26 Внешнее касание двух окружностейСкачать  |