Как найти координаты вектора и его абсолютную величину

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

1.Вектор и его абсолютная величина

Вектором называется направленный отрезок определенной длины. Любой вектор имеет начальную и конечную точки. Начало и конец вектора обозначаются заглавными буквами, например вектор

. Сам вектор обозначается прописной буквой, например:

. Каждый вектор имеет определенную длину и направление. Например, вектора

имеют одинаковое направление. А вектора

Абсолютной величиной вектора или модулем вектора называется длина отрезка, представляющего собой вектор.

Если начало вектора совпадает с его концом, то такой вектор называется нулевым.

Если два вектора имеют одинаковое направление и равные абсолютные величины, то такие векторы называются равными.

Рис.1 Обозначение векторов.

Видео:Координаты вектора.Скачать

Координаты вектора

Любой вектор имеет свои координаты. Координатами вектора называются числа x₂-x₁ и y₂-y₁. Например, координаты вектора

с начальной точкой А (1;1) и конечной точкой В (4;3) будут:

Координаты нулевого вектора равны нулю.

Абсолютная величина вектора — это его длина. А следовательно, ее можно определить как расстояние между двумя точками, начальной и конечной. Т.е.

Два вектора называются равными, если у них соответствующие координаты равны.

Рис.2 Координаты вектора.

Видео:Координаты вектора. 9 класс.Скачать

2.Сложение векторов

Пусть заданы два вектора со своими координатами

(b₁;b₂). Тогда суммой двух векторов будет вектор с координатами

В векторной форме можно записать так:

Для сложения векторов используются два метода: метод треугольника и метод параллелограмма.

Для сложения векторов методом треугольника необходимо перенести вектор

параллельным переносом так, чтобы конец вектора

совпадал с началом вектора

. Тогда начало вектора

и конец вектора

и будет сумма векторов

По методу параллелограмма, если два вектора

имеют общее начало, то суммой двух векторов будет диагональ параллелограмма, построенного на этих векторах, т.е. вектор

Разностью двух векторов

называется такой вектор

, который нужно прибавить к вектору

, чтобы получить вектор

Рис.3 Сложение векторов.

Видео:Нахождение координат вектора. Практическая часть. 9 класс.Скачать

3.Умножение вектора на число

Любой вектор с координатами (x;y) можно умножить на простое число, например λ. (Рис.3) Тогда произведением вектора на число λ будет называться вектор с координатами (λx;λy). Абсолютная величина вектора будет равна:

Для любых двух векторов

число λ можно вынести за скобку λ (

Если λ > 0, то направление вектора не изменяется, а если λ 2 и называется скалярным квадратом. Отсюда следует, что

Теорема. Скалярное произведение двух векторов равно произведению их абсолютных величин на косинус угла между ними.

Доказательство. Пусть даны два вектора а и b и угол между ними α. Тогда квадрат суммы двух векторов равен:

Следовательно, скалярное произведение двух векторов не зависит от выбора системы координат, а зависит только от их абсолютных величин. (Рис.5)

Так как координаты вектора

(b cos α; b sin α), то скалярное произведение двух векторов

Рис.5 Скалярное произведение векторов.

Отсюда вытекает следующий вывод:

если два вектора перпендикулярны, то их скалярное произведение равно нулю.

если скалярное произведение двух ненулевых векторов равно нулю, то векторы перпендикулярны.

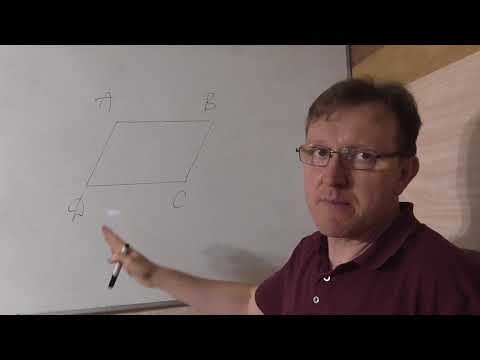
6.Пример 1

Четырехугольник ABCD — параллелограмм. Докажите равенство векторов

Доказательство:

Пусть ABCD данный параллелограмм (Рис.6). Необходимо доказать, что вектора

параллельному переносу таким образом, чтобы точка А совпала с точкой D. При таком перемещении точка А смещается по прямой AD и переходит в точку D. Это значит, что точка В переместится по параллельной прямой ВС в точку С.

Таким образом, при параллельном переносе прямая АВ переходит в параллельную прямую DC, а вектор

переходит в вектор

. А это значит, что эти вектора равны.

Действительно, так как при перемещении прямая АВ переходит в параллельную прямую DC, а точка А переходит в точку D, то на луче DC можно отложить только один вектор, равный вектору

Рис.6 Задача. Четырехугольник ABCD — параллелограмм.

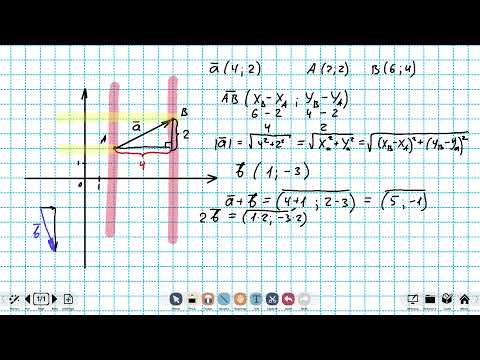
Пример 2

Даны точки А(1;1), B(3;1), C(2;-2), D(4;-2). Докажите равенство векторов

Доказательство:

Найдем координаты векторов

Таким образом, координаты векторов следующие:

А так как равные вектора имеют равные соответствующие координаты и x_AB = x_CD, y_AB = y_CD, то вектора

Рис.7 Задача. Даны точки А(1;1), B(3;1), C(2;-2), D(4;-2).

Пример 3

В треугольнике АВС проведена медиана AM. Докажите, что

Доказательство:

, равный и параллельный вектору

от точки С. И отложим вектор

, равный и параллельный вектору

от точки В (Рис.8).

Тодга получим параллелограмм, в котором вектор

, так же как вектор

. А так как диагонали параллелограмма пересекаются в точке М и делятся этой точкой пополам, то

Отсюда можно сделать вывод: так как

Рис.8 Задача. В треугольнике АВС проведена медиана AM.

Пример 4

(-3;-2). Найдите вектор

и его абсолютную величину.

Решение:

, то найдем его координаты:

Теперь найдем его абсолютную величину:

| 2 = (-1) 2 + (-4) 2 = 17

| =

(-3;-2). » alt=»Задача. Даны векторы

Рис.9 Задача. Даны векторы

Пример 5

Найдите угол между векторами

Решение:

По определению, скалярное произведение двух векторов равно произведению их абсолютных величин на косинус угла между ними. Отсюда можно найти косинус угла между ними по формуле:

Следовательно, cos α = 2 / 2 = 1 /

Таким образом, угол между векторами

(1;-1) и b (2;0).» alt=»Задача. Найдите угол между векторами

(1;-1) и b (2;0).» src=»http://www.mathtask.ru/page-0056/pl21.png»/>

Рис.10 Задача. Найдите угол между векторами

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Вектор. Координаты вектора.

В прямоугольной системе координат х0у проекции х и у вектора на оси абсцисс и ординат называются координатами вектора. Координаты вектора общепринято указывать в виде (х, у), а сам вектор как: =(х, у).

Видео:Тема 7.2. Координаты вектора. Абсолютная величина.Скачать

Формула определения координат вектора для двухмерных задач.

В случае двухмерной задачи вектор с известными координатами точек A(х₁;у₁) и B(x₂;y₂) можно вычислить:

= (x₂ – x₁ ; y₂ – y₁).

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Формула определения координат вектора для пространственных задач.

В случае пространственной задачи вектор с известными координатами точек A(х₁;у₁;z₁) и B(x₂;y₂;z₂) можно вычислить применив формулу:

= (x₂ – x₁ ; y₂ – y₁;z₂ – z₁).

Координаты дают всеобъемлющую характеристику вектора, поскольку по координатам есть возможность построить и сам вектор. Зная координаты, легко вычислить и длину вектора. (Свойство 3, приведенное ниже).

Видео:№934. Найдите координаты вектора АВ, зная координаты его начала и конца: а) А (2; 7), B (-2; 7);Скачать

Свойства координат вектора.

1. Любые равные векторы в единой системе координат имеют равные координаты.

2. Координаты коллинеарных векторов пропорциональны. При условии, что ни один из векторов не равен нулю.

3. Квадрат длины любого вектора равен сумме квадратов его координат.

4.При операции умножения вектора на действительное число каждая его координата умножается на это число.

5. При операции сложения векторов вычисляем сумму соответствующие координаты векторов.

6. Скалярное произведение двух векторов равняется сумме произведений их соответствующих координат.

Видео:Как найти координаты вектора?Скачать

Координаты вектора в декартовой системе координат (ДСК)

Для начала дадим определение координат вектора в заданной системе координат. Чтобы ввести данное понятие, определим что мы называем прямоугольной или декартовой системой координат.

Прямоугольная система координат представляет из себя прямолинейную систему координат с взаимно перпендикулярными осями на плоскости или в пространстве.

С помощью введения прямоугольной системы координат на плоскости или в трехмерном пространстве становится возможным описывание геометрических фигур вместе с их свойствами при помощи уравнений и неравенств, то есть использовать алгебраические методы при решении геометрических задач.

Тем самым, мы можем привязать к заданной системе координат векторы. Это значительно расширит наши возможности при решении определенных задач

Прямоугольная система координат на плоскости обычно обозначается O x y , где O x и O y – оси коорднат. Ось O x называют осью абсцисс, а ось O y – осью ординат (в пространстве появляется ещё одна ось O z , которая перпендикулярна и O x и O y ).

Итак, нам дана прямоугольная декартова система координат O x y на плоскости если мы отложим от начала координат векторы i → и j → , направление которых соответственно совпадет с положительными направлениями осей O x и O y , и их длина будет равна условной единице, мы получим координатные векторы. То есть в данном случае i → и j → являются координатными векторами.

Видео:Координаты вектора и действия с нимиСкачать

Координатные векторы

Векторы i → и j → называются координатными векторами для заданной системы координат.

Откладываем от начала координат произвольный вектор a → . Опираясь на геометрическое определение операций над векторами, вектор a → может быть представлен в виде a → = a x · i → + a y · j → , где коэффициенты a x и a y — единственные в своем роде, их единственность достаточно просто доказать методом от противного.

Видео:Абсолютная величина вектора. Равенство векторов.Скачать

Разложение вектора

Разложением вектора a → по координатным векторам i → и j → на плоскости называется представление вида a → = a x · i → + a y · j → .

Коэффициенты a x и a y называются координатами вектора в данной системе координат на плоскости.

Координаты вектора в данной системе координат принято записывать в круглых скобках, через запятую, при этом заданные координаты следует отделять от обозначения вектора знаком равенства. К примеру, запись a → = ( 2 ; — 3 ) означает, что вектор a → имеет координаты ( 2 ; — 3 ) в данной системе координат и может быть представлен в виде разложения по координатным векторам i → и j → как a → = 2 · i → — 3 · j → .

Следует обратить внимание, что порядок записи координат, имеет важное значение, если вы запишите координаты вектора в другом порядке, вы получите совершенно другой вектор.

Опираясь на определения координат вектора и их разложения становится очевидным, что единичные векторы i → и j → имеют координаты ( 1 ; 0 ) и ( 0 ; 1 ) соответственно, и они могут быть представлены в виде следующих разложений i → = 1 · i → + 0 · j → ; j → = 0 · i → + 1 · j → .

Также имеет место быть нулевой вектор 0 → с координатами ( 0 ; 0 ) и разложением 0 → = 0 · i → + 0 · j → .

Видео:Координаты точки и координаты вектора 1.Скачать

Равные и противоположные векторы

Векторы a → и b → равны тогда, когда их соответствующие координаты равны.

Противоположным вектором называется вектор противоположный данному.

Отсюда следует, что координаты такого вектора будут противоположны координатам данного вектора, то есть, — a → = ( — a x ; — a y ) .

Все вышеизложенное можно аналогично определить и для прямоугольной системы координат, заданной в трехмерном пространстве. В такой системе координат имеет место быть тройка координатных векторов i → , j → , k → , а произвольный вектор a → раскладывается не по двум, а уже по трем координатам, причем единственным образом и имеет вид a → = a x · i → + a y · j → + a z · k → , а коэффициенты этого разложения ( a x ; a y ; a z ) называются координатами вектора в данной (трехмерной) системе координат.

Следовательно, координатные векторы в трехмерном пространстве принимают также значение 1 и имеют координаты i → = ( 1 ; 0 ; 0 ) , j → = ( 0 ; 1 ; 0 ) , k → = ( 0 ; 0 ; 1 ) , координаты нулевого вектора также равны нулю 0 → = ( 0 ; 0 ; 0 ) , и в таком случае два вектора будут считаться равными, если все три соответствующие координаты векторов между собой равны a → = b → ⇔ a x = b x , a y = b y , a z = b z , и координаты противоположного вектора a → противоположны соответствующим координатам вектора a → , то есть, — a → = ( — a x ; — a y ; — a z ) .

Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

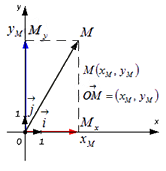
Координаты радиус-вектора точки

Чтобы ввести данное определение, требуется показать в данной системе координат связь координат точки и координат вектора.

Пусть нам дана некоторая прямоугольная декартова система координат O x y и на ней задана произвольная точка M с координатами M ( x M ; y M ) .

Вектор O M → называется радиус-вектором точки M .

Определим, какие координаты в данной системе координат имеет радиус-вектор точки

Вектор O M → имеет вид суммы O M → = O M x → + O M y → = x M · i → + y M · j → , где точки M x и M y это проекции точки М на координатные прямые Ox и Oy соответственно (данные рассуждения следуют из определения проекция точки на прямую), а i → и j → — координатные векторы, следовательно, вектор O M → имеет координаты ( x M ; y M ) в данной системе координат.

Иначе говоря, координаты радиус-вектора точки М равны соответствующим координатам точки М в прямоугольной декартовой системе координат.

Аналогично в трехмерном пространстве радиус-вектор точки M ( x M ; y M ; z M ) разлагается по координатным векторам как O M → = O M x → + O M y → + O M z → = x M · i → + y M · j → + z M · k → , следовательно, O M → = ( x M ; y M ; z M ) .

🎬 Видео

§7 Направляющие косинусы вектораСкачать

Скалярное произведение векторов через координаты. 9 класс.Скачать

9 класс, 2 урок, Координаты вектораСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Координаты вектора. Видеоурок по геометрии 9 классСкачать

Длина вектора через координаты. 9 класс.Скачать