Вектора в r2 и r3

В этой главе мы возвращаемся к более конкретному понятию: вектор — направленный отрезок. Будем рассматривать направленные отрезки, расположенные не только на плоскости, но и в обычном трёхмерном пространстве. В математике, физике и их приложениях понятие вектора используется очень широко. Векторами изображаются, например, скорость и сила. С другой стороны, величины, определяемые лишь числом (и не имеющие направления), называются скалярами. Примеры скалярных величин: масса, объём.

4.1. Векторы в трёхмерном пространстве

4.1.1. Линейное пространство направленных отрезков R 3

Основные понятия для векторов в трёхмерном пространстве вводятся так же, как это сделано для векторов на плоскости в разделе 3.1. Определения длины вектора, равных векторов, коллинеарных векторов, суммы векторов и произведения вектора на число не отличаются от аналогичных определений для векторов на плоскости.

Теорема 1. Множество R 3 направленных отрезков в трёхмерном пространстве с операциями сложения и умножения на число образует линейное пространство над полем действительных чисел.

Доказательство должно содержать проверку 8 аксиом линейного пространства. Такая проверка была проведена в разделе 3.1 для векторов на плоскости. Но в точности те же рассуждения справедливы и для векторов из R 3 .

Линейные пространства R 2 , R 3 являются хорошими, наглядными примерами. С их помощью мы сможем лучше освоить наиболее важные понятия общей теории линейных пространств.

Векторы a1, a2, . an из R 3 называются компланарными, если они параллельны одной и той же плоскости. Заметим, что 2 вектора всегда компланарны: если их отложить из одной точки, то через неё и концы векторов всегда можно провести плоскость.

Теорема 2. Три вектора в R 3 линейно зависимы ⇔ они компланарны.

Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Тема 2. Лекция 6. Векторное пространство

Лекция 6. Векторное пространство.

1. Векторное линейное пространство.

2. Базис и размерность пространства.

3. Ориентация пространства.

4. Разложение вектора по базису.

5. Координаты вектора.

1. Векторное линейное пространство.

Множество, состоящее из элементов какой угодно природы, в которых определены линейные операции : сложение двух элементов и умножение элемента на число называются пространствами, а их элементы – векторами этого пространства и обозначаются так же, как и векторные величины в гео-метрии : . Векторы таких абстрактных пространств, как правило, ничего общего не имеют с обычными геометрическими векторами. Элемен-тами абстрактных пространств могут быть функции, система чисел, матрицы и т. д., а в частном случае и обычные векторы. Поэтому такие пространства принято называть векторными пространствами .

Векторными пространствами являются, например , множество колли-неарных векторов, обозначаемое V1 , множество компланарных векторов V2, множество векторов обычного (реального пространства) V3 .

Для этого частного случая можно дать следующее определение век-торного пространства.

Определение 1. Множество векторов называется векторным прост-ранством , если линейная комбинация любых векто-ров множества также является вектором этого мно-жества. Сами векторы называются элементами век-торного пространства.

Более важным как в теоретическом, так и в прикладном отношении яв-ляется общее (абстрактное) понятие векторного пространства.

Определение 2. Множество R элементов , в котором для лю-бых двух элементов и определена сум-ма и для любого элемента и любого действительного числа λ определено произведение называется векторным (или линейным) про-странством , а его элементы – векторами, если опера-ции сложения векторов и умножение вектора на число удовлетворяют следующим условиям (аксиомам) :

1) сложение коммутативно, т. е. ;

2) сложение ассоциативно, т. е. ;

3) существует такой элемент (нулевой вектор), что для любого ;

4) для каждого вектора существует противопо-ложный вектор —, такой что ;

5) для любых векторов и и любого чис-ла λ имеет место равенство ;

6) для любых векторов и любых чисел λ и µ справедливо равенство ;

7) для любого и любых чисел λ и µ справедли-во ;

8) для любого .

Из аксиом, определяющих векторное пространство, вытекают прос-тейшие следствия :

1. В векторном пространстве существует только один нуль – элемент – нулевой вектор.

2. В векторном пространстве каждый вектор имеет единственный проти-воположный вектор.

3. Для каждого элемента выполняется равенство .

4. Для любого действительного числа λ и нулевого вектора выпол-няется равенство .

5. Из равенства следует одно из двух равенств:

6. Вектор является противоположным для любого вектора .

Существование противоположного вектора определяет возможность вве-дения для вектора рассматриваемого пространства операцию вычитания как операцию, обратную операции сложения.

Разностью векторов называется вектор , удовлетворяющий равенству .

Разность векторов обозначается так : .

Итак, действительно, и множество всех геометрических векторов являет-ся линейным (векторным) пространством, так как для элементов этого мно-жества определены действия сложения и умножения на число, удовлетворя-ющие сформулированным аксиомам.

2. Базис и размерность пространства.

Существенными понятиями векторного пространства являются понятия базиса и размерность.

Определение. Совокупность линейно независимых векторов, взятых в определенном порядке, через которые линейно выражается любой вектор пространства, называется базисом этого пространства. Векторы. Составляющие базис пространства, называется базисным .

Базисом множества векторов, расположенных на произвольной прямой, можно считать один коллинеарный этой прямой вектор .

Базисом на плоскости назовем два неколлинеарных вектора на этой пло-скости, взятые в определенном порядке .

Базисом в обычном пространстве – три некомпланарных вектора, взя-тые в определенном порядке .

Если базисные векторы попарно перпендикулярны (ортогональны), то базис называется ортогональным , а если эти векторы имеют длину, равную единице, то базис называется ортонормированным .

Наибольшее число линейно независимых векторов пространства называ-ется размерностью этого пространства, т. е. размерность пространства сов-падает с числом базисных векторов этого пространства.

Итак, в соответствии с данными определениями :

1. Одномерным пространством V1 является прямая линия, а базис состо-ит из одного коллинеарного вектора .

2. Двумерным пространством V2 является плоскость, базис этого прост-ранства состоит из двух неколлинеарных векторов .

3. Обычное пространство является трехмерным пространством V3 , базис которого состоит из трех некомпланарных векторов .

Отсюда мы видим, что число базисных векторов на прямой, на плос-кости, в реальном пространстве совпадает с тем, что в геометрии принято на-зывать числом измерений (размерностью) прямой, плоскости, пространства. Поэтому естественно ввести более общее определение.

Определение. Векторное пространство R называется n – мерным, если в нем существует не более n линейно неза-висимых векторов и обозначается R n . Число n на-зывается размерностью пространства.

В соответствии с размерностью пространства делятся на конечномерные и бесконечномерные . Размерность нулевого пространства по определению считается равной нулю.

Замечание 1. В каждом пространстве можно указать сколько угодно базисов, но при этом все базисы данного пространства состоят из одного и того же числа векторов.

Замечание 2. В n – мерном векторном пространстве базисом назы-вают любую упорядоченную совокупность n линейно независимых векторов.

3. Ориентация пространства.

Пусть базисные векторы в пространстве V3 имеют общее начало и упорядочены, т. е. указано какой вектор считается первым, какой – вторым и какой – третьим. Например, в базисе век-торы упорядочены согласно индек-сации.

Для того чтобы ориентировать пространство, необходимо задать какой-нибудь базис и объявить его положительным .

Можно показать, что множество всех базисов пространства распадается на два класса, т. е. на два непересекающихся подмножества.

а) все базисы, принадлежащие одному подмножеству (классу), имеют одинаковую ориентацию (одноименные базисы) ;

б) всякие два базиса, принадлежащие различным подмножествам (кла-ссами), имеют противоположную ориентацию, (разноименные базисы) .

Если один из двух классов базисов пространства объявлен положитель-ным, а другой – отрицательным, то говорят, что это пространство ориенти-ровано .

Часто при ориентации пространства одни базисы называют правыми , а другие – левыми .

Согласно критерию наблюдателя базис называют правым , если при наблюдении с конца третьего вектора кратчайший поворот пер-вого вектора ко второму вектору осуществляется против часовой стрелки (рис. 1.8, а).

Рис. 1.8. Правый базис (а) и левый базис (б)

Обычно положительным базисом объявляется правый базис пространства

Правый (левый) базис пространства может быть определен и с помощью правила «правого» («левого») винта или буравчика.

По аналогии с этим вводится понятие правой и левой тройки некомпла-нарных векторов , которые должны быть упорядочены (рис.1.8).

Таким образом, в общем случае две упорядоченные тройки некомпла-нарных векторов имеют одинаковую ориентацию (одноименны) в пространстве V3 если они обе правые или обе левые, и – противоположную ориентацию (разноименны), если одна из них правая, а другая левая.

Аналогично поступают и в случае пространства V2 (плоскости).

4. Разложение вектора по базису.

Этот вопрос для простоты рассуждений рассмотрим на примере трех-мерного векторного пространства R3 .

Пусть — линейно независимые векторы (базис) пространства R3 а — произвольный вектор этого пространства.

Теорема. Любой вектор пространства R3 однозначно представим в виде линейной комбинации трех линейно независимых век-торов этого пространства, т. е.

(3)

Представление произвольного вектора в виде линейной комбинации ба-зисных векторов называется разложением этого вектора по базису.

Например, выражение означает, что вектор разложен по базису .

5. Координаты вектора.

5.1. Понятие о координатах вектора.

Из рассмотренного выше следует, что фиксированный базис позволяет сопоставить каждому вектору пространства R 3 упорядоченную тройку чисел (а пространству R 2 – плоскости, — упорядоченную двойку чисел), которые являются коэффициентами разложения этого вектора по векторам базиса. Наоборот, каждой упорядоченной тройке чисел при помощи бази-са сопоставляется единственный вектор пространства, если составим линейную комбинацию (аналогично и для пространства R 2 и вообще R n ).

Определение. Если — базис и вектор , то числа называются координатами вектора в данном базисе.

Обозначение : или, в конкретном случае .

Вполне очевидно, что если в пространстве R выбрать другой базис, то тот же вектор будет иметь другие координаты.

5.2. Условие коллинеарности двух векторов.

Пусть векторы и разложены по базису :

Известно, что два вектора коллинеарны тогда и только тогда, когда они линейно зависимы, т. е. , где хотя бы одно из чисел λ1 или λ2 отличны от нуля.

Для определенности положим . Тогда

Откуда соотношение между координатами векторов (на основе аксиомы 5)

или их отношения

(7) Следовательно, необходимым и достаточным условием коллинеарности двух векторов является пропорциональность их соответствующих координат в данном базисе.

1. Векторное пространство характеризуется размерностью, базисом и ориентацией.

2. Каждый вектор пространства R n разлагается по его базису единствен-

ственным способом, коэффициенты при базисных векторах в этом разложе-нии называются координатами вектора.

Видео:Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Введение в R: линейная алгебра

R — очень мощный язык, разработанный специально для анализа и визуализации данных и машинного обучения, что делает его обязательным к изучению для любого начинающего специалиста по данным.

R особенно удобен для линейной алгебры. Встроенные типы данных, такие как векторы и матрицы, хорошо сочетаются со встроенными функциями, такими как алгоритмы решения собственных значений и определителей, а также с возможностями динамического индексирования.

В этой вводной в статье про R рассмотрим следующие реализации линейной алгебры:

Векторы

• присваивание векторов;
• векторные операции;
• генерирование последовательностей;
• логические векторы;
• пропущенные значения;
• индексирование векторов.

Массивы и матрицы

• массивы;
• индексация массивов;
• индексация матриц;
• внешнее произведение двух матриц;
• демонстрация всех возможных определителей одноразрядных матриц 2×2;
• обобщённое транспонирование массива;
• умножение матриц;
• линейные уравнения и инверсия;
• собственные значения и собственные векторы;
• сингулярное разложение и определители;
• выравнивание методом наименьших квадратов и QR-разложение;
• формирование блочных матриц.

Видео:Как разложить вектор по базису - bezbotvyСкачать

Векторы

Присваивание векторов

R оперирует структурами данных, самой простой из которых является числовой вектор — упорядоченный набор чисел. Чтобы создать вектор x с четырьмя элементами 1 , 2 , 3 и 4 , можно использовать объединяющую функцию c() .

Здесь используется оператор присваивания , указывающий на назначаемый объект. В большинстве случаев можно заменить на = .

Также можно использовать функцию assign() :

Оператор y присвоит вектор 1, 2, 3, 4, 0, 1, 2, 3, 4 переменной y .

Векторы можно свободно перемножать и дополнять константами:

Заметьте, что эта операция верна, даже когда x и y имеют разную длину. В данном случае R просто будет повторять x (иногда дробно), пока не достигнет длины y. Поскольку y равен 9 числам в длину, а x — 4, x повторится 2.25 раз пока не совпадёт с длиной y.

Можно использовать все арифметические операторы: + , — , * , / и ^ , а также log , exp , sin , cos , tan , sqrt и многие другие. max(x) и min(x) отображают наибольший и наименьший элементы вектора x , а length(x) — количество элементов x ; sum(x) выдаёт сумму всех элементов x , а prod(x) — их произведение.

mean(x) вычисляет выборочное среднее, var(x) возвращает выборочную дисперсию, sort(x) возвращает вектор того же размера, что и x, элементы в котором расположены в порядке возрастания.

Генерация последовательностей

В R существует множество методов для генерации последовательностей чисел. 1:30 аналогичен c(1, 2, …, 29, 30) . Двоеточие имеет более высокий приоритет в выражении, поэтому 2*1:15 вернёт c(2, 4, …, 28, 30) , а не c(2, 3, …, 14, 15) .

30:1 используется для генерации последовательности в обратном направлении.

Для генерации последовательностей можно использовать и функцию seq() . seq(2,10) возвращает такой же вектор, что и 2:10 . В seq() , можно также указать длину шага: seq(1,2,by=0.5) возвращает c(1, 1.5, 2) .

Аналогичная функция rep() копирует объект различными способами. Например, rep(x, times=5) вернёт пять копий x впритык.

Логические векторы

Логические значения в R — TRUE, FALSE и NA. Логические векторы задаются условиями. val 13 задаёт val в качестве вектора той же длины, что x , со значением TRUE , если условие выполняется, и FALSE , если нет.

Логические операторы в R: , , > , >= , == и != , означающие, соответственно, меньше чем, меньше чем или равно, больше чем, больше чем или равно, равно или не равно.

Пропущенные значения

Функция is.na(x) возвращает логический вектор того же размера, что и x , со значение TRUE , если соответствующий элемент для x равен NA .

x == NA отличается от is.na(x) , поскольку NA является не значением, а маркером для недоступной величины.

Второй тип “пропущенного значения” создаётся численными вычислениями, например 0/0 . В этом случае значения NaN (не числа) рассматриваются как значения NA , то есть is.na(x) вернёт TRUE и для NA , и для NaN значений. is.nan(x) используется только для определения значений NaN .

Индексирование векторов

Первый вид индексации — через логический вектор. y устанавливает y значениям x , не равным NA или NaN .

(x+1)[(!is.na(x)) & x>0] -> z устанавливает z значениям x+1 , больше 0 и не являющимся Na или NaN .

Второй метод осуществляется с вектором положительных целых значений. В этом случае значения должны быть в наборе . Для формирования результата соответствующие элементы вектора выбираются и объединяются в этом порядке. Важно помнить, что, в отличие от других языков, в R первый индекс равен 1, а не 0.

x[1:10] возвращает первые 10 элементов x , предполагая, что length(x) не менее 10. c(‘x’, ‘y’)[rep(c(1,2,2,1), times=4)] создаёт символьный вектор длиной 16, где ‘x’, ‘y’, ‘y’, ‘x’ повторяются четыре раза.

Вектор отрицательных целых чисел определяет значения, которые должны быть исключены. y устанавливает y всем значениям x , кроме первых пяти.

Наконец, вектор символьных строк может использоваться, когда у объекта есть атрибут name для идентификации его компонентов. Для можно задать имя каждому индексу вектора names(fruit) . Затем элементы можно вызывать по имени lunch .

Преимущество этого подхода в том, что иногда буквенно-цифровые имена запомнить легче, чем индексы.

Обратите внимание, что индексированное выражение может встречаться на принимающей стороне присвоения, где оно только для этих элементов вектора. Например, x[is.na(x)] заменяет все значения NA и NaN в векторе x на 0 .

Другой пример: y[y аналогичен y — код просто заменяет все значения меньше 0 на отрицательные значения.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Массивы и матрицы

Массивы

Массив — это проиндексированный набор записей данных, не обязательно численный.

Вектор размерности — это вектор неотрицательных чисел. Если длина равна k, тогда массив k-размерный. Размерности индексируются от единицы вверх до значения, указанного вектором размерности.

Вектор может использоваться R в качестве массива, как атрибут dim . Если z — вектор из 1500 элементов, присвоение dim(z) означает, что z теперь представлен как массив 100 на 5 на 3.

Индексирование массивов

На индивидуальные элементы массива можно ссылаться, указав имя массива и в квадратных скобках индексы, разделённые запятыми.

Первое значение вектора a — 3 на 4 на 6 — может быть вызвано как a[1, 1, 1] , а последнее как a[3, 4, 6] .

a[,,] отображает массив полностью, следовательно, a[1,1,] берёт первую строку первого 2-размерного сечения a .

Индексирование матриц

Следующий код генерирует массив 4 на 5: x .

Массивы определяются вектором значений и размерностью матрицы. Значения вычисляются сначала сверху вниз, затем слева направо.

array(1:4, dim = c(2,2)) вернёт

В матрицах индексов запрещены отрицательные индексы, а значения NA и ноль разрешены.

Внешнее произведение двух матриц

Важной операцией с векторами является внешнее произведение. Если a и b — это два численных массива, их внешним произведением является массив, вектор размерности которого получается объединением двух векторов размерности, а вектор данных достигается формированием всех возможных произведений элементов вектора данных a и элементов вектора b . Внешнее произведение вычисляется с помощью оператора %o% :

Фактически любую функцию можно применить к двум массивам, используя внешнюю () функцию. Предположим, мы определили функцию f . Функцию можно применить к двум векторам x и y с помощью z .

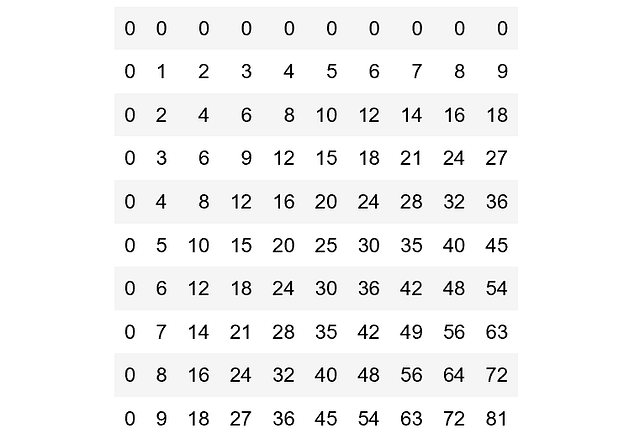
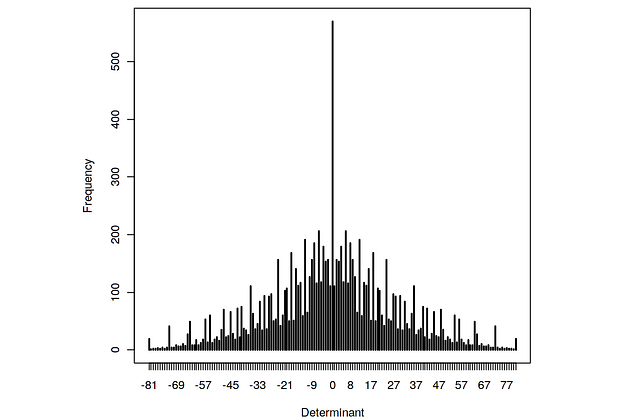
Демонстрация всех возможных определителей одноразрядных матриц 2×2

Рассмотрим определители матриц 2 на 2 [a, b; c, d], где каждая запись представляет собой неотрицательное число от 0 до 9. Задача: найти определители всех возможных матриц этой формы и отобразить на графике высокой плотности частоту, с которой встречается значение.

Или, перефразируя, нужно найти распределение вероятности определителя, если каждая цифра выбирается независимо и равномерно случайным образом.

Один из умных способов сделать это — использовать внешнюю функцию дважды.

Первая строка присваивает d этой матрице:

Вторая строка снова использует внешнюю функцию для расчёта всех возможных определителей. Последняя строка строит график.

Обобщённое транспонирование массива

Функция aperm(a, perm) используется для перестановки массива a. Аргументом perm должна быть перестановка чисел <1,…, k>, где k — количество индексов в a. Результатом функции будет массив того же размера, что и a, но прежняя размерность, заданная perm[j] , становится новой размерностью j-th .

Проще понять, если думать об этом как об обобщённом транспонировании матриц. Если A — это матрица, тогда B — просто результат перестановки матрицы A :

В таких особых случаях перестановку осуществляет функция t() .

Умножение матриц

Для умножения матриц используется оператор %*% . Если A и B являются квадратными матрицами одинакового размера, A*B — это поэлементное произведение двух матриц. A %*% B — это скалярное произведение (произведение матриц).

Если x — вектор, тогда x %*% A %*% x — его квадратичная форма.

crossprod() осуществляет перекрёстные произведения. Таким образом crossprod(X, y) аналогична операции t(X) %*% y , но более эффективна.

diag(v) , где v — вектор — задаёт диагональную матрицу с элементами вектора в качестве диагональных элементов. diag(M) , где m — матрица — задаёт вектор основных диагональных элементов M (так же как и в Matlab). diag(k) , где k — единичное числовое значение — возвращает единичную матрицу k на k .

Линейные уравнения и инверсия

Решение линейных уравнений является инверсией умножения матриц. Если

с заданными только A и b , вектор x — решение системы линейных уравнений, которое быстро решается в R:

Собственные значения и собственные векторы

Функция eigen(Sm) вычисляет собственные значения и собственные векторы симметричной матрицы Sm. Результат — это список, где первый элемент отображает значения, а второй — векторы. ev присваивает этот список ev .

ev$val — это вектор собственных значений Sm , и ev$vec — матрица соответствующих собственных векторов.

Для больших матриц лучше избегать вычисления собственных векторов, если они не нужны, используя выражение:

Сингулярное разложение и определители

Функция svd(m) принимает произвольный матричный аргумент m и вычисляет его сингулярное разложение. Оно состоит из 1) матрицы ортонормированных столбцов U с тем же пространством столбцов, что и m , 2) второй матрицы ортонормированных столбцов V , пространство столбцов которой является пространством строк m , 3) и диагональной матрицы положительных элементов D :

det(m) используется для вычисления определителя квадратной матрицы m .

Выравнивание методом наименьших квадратов и QR-разложение

Функция lsfit() возвращает список заданных результатов процедуры выравнивания методом наименьших квадратов. Присваивание наподобие этого:

выдаёт результаты выравнивания методом наименьших квадратов, где y — это вектор наблюдений, а X — проектная матрица.

ls.diag() используется для диагностики регрессии.

Тесно связанной функцией является qr().

Они вычисляют ортогональную проекцию y на диапазон X в fit , проекцию на ортогональное дополнение в res и вектор коэффициентов для проекции в b .

Формирование блочных матриц

Матрицы можно строить из других векторов и матриц с помощью функций cbind() и rbind() .

cbind() формирует матрицы, связывая матрицы горизонтально (поколоночно), а rbind() связывает матрицы вертикально (построчно).

В присвоении X аргументами cbind() должны быть либо векторы любой длины, либо столбцы одинакового размера (одинаковым количеством строк).

rbind() выполняет соответствующую операцию для строк.

📸 Видео

Базис. Разложение вектора по базису.Скачать

Разложение вектора по базису. 9 класс.Скачать

Найдите разложение вектора по векторам (базису)Скачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

18+ Математика без Ху!ни. Векторное произведение.Скачать

Радиус векторСкачать

Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Единичный векторСкачать

Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

КООРДИНАТЫ ВЕКТОРА В ПРОСТРАНСТВЕ решение задачСкачать

Образуют ли данные векторы базисСкачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать