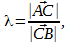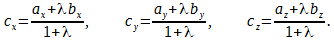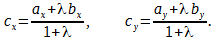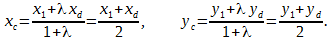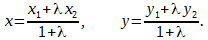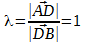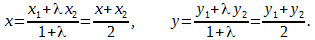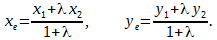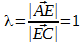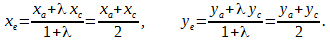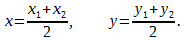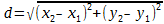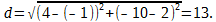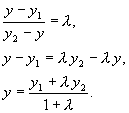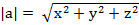Как найти координаты точки делящей вектор пополам (8 видео)

Деление отрезка в заданном соотношении: координаты точки

Когда существуют условия деления отрезка в определенном отношении, необходимо уметь определять координаты точки, служащей разделителем. Выведем формулу для нахождения этих координат, поставив задачу на плоскости.

Содержание

Определение координат точки, делящей отрезок в заданном отношении, на плоскости
Определение координат точки, делящей отрезок в заданном отношении, в пространстве
Деление векторов в данном соотношении
Примеры решения заданий по делению векторов и отрезков
Декартова прямоугольная система координат. Деление отрезка в данном отношении.
📸 Видео

Видео:Координаты середины отрезкаСкачать

Определение координат точки, делящей отрезок в заданном отношении, на плоскости

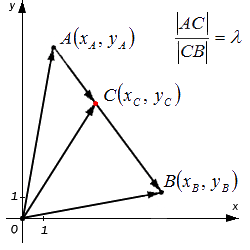
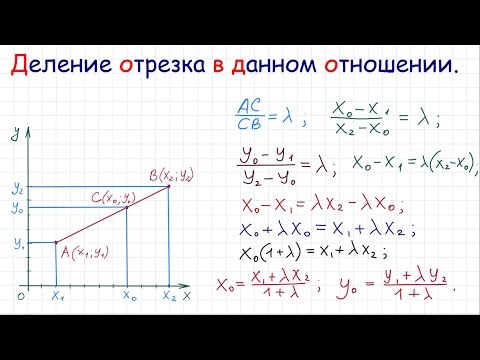
Исходные данные: задана прямоугольная система координат O x y и две лежащие на ней, несовпадающие точки с заданными координатами A ( x A , y A ) и B ( x B , y B ) . А также задана точка С , делящая отрезок А В в отношении λ (некоторое положительное действительное число). Необходимо определить координаты точки С : x C и y C .

Перед тем, как приступить к решению поставленной задачи, немного раскроем смысл заданного условия: «точка С , делящая отрезок А В в отношении λ ». Во-первых, это выражение свидетельствует о том, что точка С лежит на отрезке А В (т.е. между точками А и В ). Во-вторых, понятно, что согласно заданному условию отношение длин отрезков А С и С В равно λ . Т.е. верно равенство:

В этом случае точка А – начало отрезка, точка В – конец отрезка. Если бы было задано, что точка С делит в заданном отношении отрезок В А , тогда верным было бы равенство: .

Ну и совсем очевидный факт, что если λ = 1 , то точка С является серединой отрезка А В .

Решим поставленную задачу при помощи векторов. Отобразим произвольно в некой прямоугольной системе координат точки А , В и точку С на отрезке А В . Построим радиус-векторы указанных точек, а также векторы A C → и C B → . Согласно условиям задачи, точка С делит отрезок А В в отношении λ .

Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = ( x A , y A ) и O B → = ( x B , y B ) .

Определим координаты вектора : они будут равны координатам точки С , которые и требуется найти по условию задачи.

Используя операцию сложения векторов, запишем равенства: O C → = O A → + A C → O B → = O C → + C B → ⇔ C B → = O B → — O C →

По условию задачи точка С делит отрезок А В в отношении λ , т.е. верно равенство A C = λ · C B .

Векторы A C → и C B → лежат на одной прямой и являются сонаправленными. λ > 0 по условию задачи, тогда, согласно операции умножения вектора на число, получим: A C → = λ · C B → .

Преобразуем выражение, подставив в него : C B → = O B → — O C → .

A C → = λ · ( O B → — O C → ) .

Равенство O C → = O A → + A C → перепишем как O C → = O A → + λ · ( O B → — O C → ) .

Используя свойства операций над векторами, из последнего равенства следует: O C → = 1 1 + λ · ( O A → + λ · O B → ) .

Теперь нам остается непосредственно вычислить координаты вектора O C → = 1 1 + λ · O A → + λ · O B → .

Выполним необходимые действия над векторами O A → и O B → .

O A → = ( x A , y A ) и O B → = ( x B , y B ) , тогда O A → + λ · O B → = ( x A + λ · x B , y A + λ · y B ) .

Таким образом, O C → = 1 1 + λ · ( O A → + λ · O B → ) = ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ ) .

Резюмируя: координаты точки С , делящей отрезок А В в заданном отношении λ определяются по формулам : x C = x A + λ · x B 1 + λ и y C = у A + λ · y B 1 + λ .

Видео:Деление отрезка в данном отношенииСкачать

Определение координат точки, делящей отрезок в заданном отношении, в пространстве

Исходные данные: прямоугольная система координат O x y z , точки с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) .

Точка С делит отрезок А В в отношении λ . Необходимо определить координаты точки С .

Используем ту же схему рассуждений, что и в случае выше на плоскости, придем к равенству:

O C → = 1 1 + λ · ( O A → + λ · O B → )

Векторы и являются радиус-векторами точек А и В , а значит:

O A → = ( x A , y A , z A ) и O B → = ( x B , y B , z B ) , следовательно

O C → = 1 1 + λ · ( O A → + λ · O B → ) = ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ , z A + λ · z B 1 + λ )

Таким образом, точка С , делящая отрезок А В в пространстве в заданном отношении λ , имеет координаты: ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ , z A + λ · z B 1 + λ )

Рассмотрим теорию на конкретных примерах.

Исходные данные: точка С делит отрезок А В в отношении пять к трем. Координаты точек А и В заданы A ( 11 , 1 , 0 ) , B ( — 9 , 2 , — 4 ) .

Решение

По условию задачи λ = 5 3 . Применим полученные выше формулы и получим:

x A + λ · x B 1 + λ = 11 + 5 3 · ( — 9 ) 1 + 5 3 = — 3 2

y A + λ · y B 1 + λ = 1 + 5 3 · 2 1 + 5 3 = 13 8

z A + λ · z B 1 + λ = 0 + 5 3 · ( — 4 ) 1 + 5 3 = — 5 2

Ответ: C ( — 3 2 , 13 8 , — 5 2 )

Исходные данные: необходимо определить координаты центра тяжести треугольника А В С .

Заданы координаты его вершин: A ( 2 , 3 , 1 ) , B ( 4 , 1 , — 2 ) , C ( — 5 , — 4 , 8 )

Решение

Известно, что центром тяжести любого треугольника является точка пересечения его медиан (пусть это будет точка М ). Каждая из медиан делится точкой М в отношении 2 к 1 , считая от вершины. Исходя из этого, найдем ответ на поставленный вопрос.

Допустим, что А D – медиана треугольника А В С . Точка М – точка пересечения медиан, имеет координаты M ( x M , y M , z M ) и является центром тяжести треугольника. М , как точка пересечения медиан, делит отрезок А D в отношении 2 к 1 , т.е. λ = 2 .

Найдем координаты точки D . Так как A D – медиана, то точка D – середина отрезка В С . Тогда, используя формулу нахождения координат середины отрезка, получим:

x D = x B + x C 2 = 4 + ( — 5 ) 2 = — 1 2 y D = y B + y C 2 = 1 + ( — 4 ) 2 = — 3 2 z D = z B + z C 2 = — 2 + 8 2 = 3

Вычислим координаты точки М :

x M = x A + λ · x D 1 + λ = 2 + 2 · ( — 1 2 ) 1 + 2 = 1 3

y M = y A + λ · y D 1 + λ = 3 + 2 · ( — 3 2 ) 1 + 2 = 0

z M = z A + λ · z D 1 + λ = 1 + 2 · 3 1 + 2 = 7 3

Видео:#2 Как найти координаты точки K, делящей отрезок AB в отношении m:n?Скачать

Деление векторов в данном соотношении

Пусть вектор 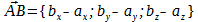задан координатами своего начала A(a_x; a_y; a_z) и конца B(b_x; b_y; b_z) и пусть точка C(c_x; c_y; c_z) расположена между точка A и B

пусть при этом известно соотношение длин векторов

тогда координаты точки C(c_x; c_y; c_z) находятся по формулам

Видео:Деление отрезка в данном отношении. 8 класс.Скачать

Примеры решения заданий по делению векторов и отрезков

Отрезок AB точками C(3, 4) и D(5, 6) разделён на три равные части. Найти координаты точек A и B.

Р е ш е н и е. Обозначим координаты точек A и B так: А(x1, y1), B(x1, y1). Для отрезка AD точка C является серединой, потому λ = AC / CD = 1 и по формулам деления отрезка в данном соотношении

Подставим в последнее равенство координаты x_c, y_c, x_d, y_d:

3 = (x1 + 5)/2, 4 = (y1 + 6)/2,

откуда находим, x₁ = 1, y₁ = 2. Точка A имеет координаты A(1, 2).

Поскольку точка D есть середина отрезка CB, то x_d = (x_c + x₂)/2, или 5 = (3 + x₂)/2, отсюда x₂ = 7.

отсюда y₂ = 8. Получили B(7, 8).

О т в е т: A(1, 2), B(7, 8).

Даны вершины треугольника A(2, -4), B(4, -5) и C(-4, 7). Определить середины его сторон.

Р е ш е н и е. Воспользуемся формулой для определения середин сторон отрезка, при известных двух точках:

Поскольку отрезки делятся на равные части, то

Тогда формула приобретает вид:

Координата x для отрезка AB равна (2+4)/2 = 3, координата y для отрезка AB равна (-4-5)/2 = -4,5.

Координата x для отрезка AC равна (2-4)/2 = -1, координата y для отрезка AC равна (-4+7)/2 = 1,5.

Координата x для отрезка BC равна (4-4)/2 = 0, координата y для отрезка BC равна (-5+7)/2 = 1.

О т в е т: искомые точки имеют координаты (3; -4,5), (-1; 1,5) и (0; 1).

Даны три вершины параллелограмма A(2, -4), B(4, -2), C(-2, 4). Определить четвёртую вершину D, противоположную B.

Р е ш е н и е. Найдём точку, в которой пересекаются диагонали параллелограмма.

Назовём точку пересечения диагоналей точкой E.

Поскольку этой точкой диагонали делятся на два равных отрезка

то формула приобретает вид:

Найдём середину отрезка AC:

Итак, точка E имеет координаты (0, 0).

Данная точка также является серединой отрезка BD, поскольку это вторая диагональ параллелограмма. Тогда

подставим известные значения:

Теперь найдём вторую координату:

подставим известные значения:

Даны вершины треугольника A(2, 3); B(4, -10); C(-4, 1), определить длину его медианы, проведённой из вершины B.

Р е ш е н и е. Назовём точку пересечения медианы и стороны AC точкой D. Поскольку медиана делит сторону треугольника пополам, то воспользуемся формулой нахождения координат точки посередине отрезка:

Точка D имеет координаты (-1, 2).

Воспользуемся формулой нахождения длины отрезка, когда известны координаты его крайних точек:

О т в е т: Длина медианы, проведённой из вершины B, равна 13.

Видео:Деление отрезка в данном отношении. 11 класс.Скачать

Декартова прямоугольная система координат. Деление отрезка в данном отношении.

Декартова прямоугольная система координат

Определение 1. Осью называется прямая, на которой:

1) выбрана начальная точка («начало» — точка О);

2) указано (стрелкой) положительное направление отсчета;

3) выбран масштаб.

Определение 2. Декартовой прямоугольной системой координат на плоскости (в пространстве) называют две (три) взаимно перпендикулярные оси с общим началом. Первая ось OX называется осью абсцисс, вторая ось OY — осью ординат (третья ось OZ — осью аппликат).

Каждой точке плоскости (пространства) ставится в соответствие упорядоченная пара (тройка) действительных чисел — координат данной точки.

Определение 3. Уравнением линии на плоскостиназывается уравнение с двумя переменными, такое, что только координаты любой точки, лежащей на этой линии, удовлетворяют данному уравнению.

Расстояние между двумя точками на плоскости

Из треугольника ABC:

Деление отрезка в данном отношении

Пусть даны две точки M₁ (x₁, y₁) и M₂ (x₂, y₂). Найдем на отрезке M₁M₂ точку N, которая делила бы данный отрезок в отношении : .

B₂ M₂

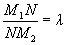
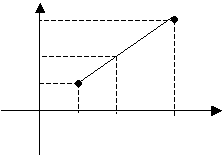
По теореме о пропорциональности отрезков прямых, пересеченных рядом параллельных прямых, получим

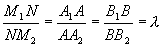
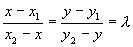
Координаты точки, делящей отрезок в данном отношении, находятся по этим формулам.

Если l = 1 , то деление отрезка производится пополам:

, — формулы для нахождения координат середины отрезка.

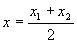
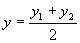
Скалярное произведение векторов; скалярное произведение векторов, заданных координатами.

Скалярное произведение векторов.

Скалярным произведением вект. А и В называется число, равное произведению длин этих векторов, умноженному на косинус угла между ними

Свойства. 1) (a,b)=(b,a) (коммутативность). 2) (λa,b) =(a, λb) = λ (a,b) (ассоциативность). 3) дистрибутивно относительно сумсуммы (а+b,с)=(а,b)+(а,с) 4) Скалярное произведение двух векторов равно нулю тогда и только тогда когда хотя бы один из вект. нулевой либо они перпендикулярны (a • b = 0, если a ┴ b).

Скалярным квадратом называется скалярное произведение вектора на себя => равен квадрату длины вектора.

(a,b)= *|b|*Cos(a^b); пр_ab=(a,b)/ (проекция a на b). Длина

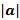
Скалярное произведение в коорд форме.Коорд орты i,j,k имеют длины, равные единицы i 2 =j 2 =k 2 =1, их взаимное произведение равно 0 . (a,b) =a_x*b_x+a_y*b_y+a_z*b_z. Cos и ПР находятся с помощью координат.

Векторное произведение векторов.
Векторным произведением вектора а на вектор b называется вектор с, который: 1) Перпендикулярен векторам a и b, т. е. с^а и с^b; 2) Имеет длину, численно равную площади параллелограмма, построенного на векторах а и b как на сторонах, т. е. 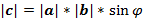. 3.Векторы a, b и с образуют правую тройку.

Свойства: 1. При перестановке сомножителей векторное произведение меняет знак, т.е. [а,b] =[b,a]; 2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. [а,b] = [а,b] = [b,a]; 3. Два ненулевых вектора а и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. а||b [а,b] =0. 4.распределительное свойство:[a+b,с]=[а,с]+[b,с].