Как найти хорду вписанной окружности в треугольник

Хорда — отрезок соединяющий любые две точки окружности. Диаметр окружности, самая большая хорда.

L — хорда

R — радиус окружности

O — центр окружности

α — центральный угол

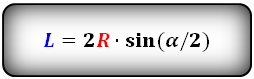
Формула длины хорды, ( L ):

Калькулятор для расчета длины хорды окружности :

Дополнительные формулы для окружности:

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Треугольник вписанный в окружность

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Видео:Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать

Как найти хорду вписанной окружности в треугольник

Видео:ЕГЭ-2022 ||Задание №6 || Найти длину хордыСкачать Определение хорды Хорда — это отрезок, который соединяет две точки заданной кривой. Хорда может быть у дуги, окружности, эллипса и т.д. На рисунке хорда обозначена как отрезок AB красного цвета . Оба его конца находятся на окружности Часть кривой, заключенной между двумя точками хорды, называется дугой. На рисунке дуга хорды AB обозначена зеленым цветом . Плоская фигура, заключенная между дугой и ее хордой называется сегментом. Сегмент на рисунке ограничен красным отрезком AB с одной стороны, и зеленой дугой — с другой стороны. Хорда, проходящая через центр окружности, называется диаметром окружности. Диаметр окружности — самая длинная хорда окружности. Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать Свойства хорды к окружности Если расстояния от центра окружности до хорд равны, то эти хорды равны. Верно и обратное — если хорды равны, то расстояния от центра окружности до этих хорд равны Если хорда больше, то расстояние от центра окружности до этой хорды меньше. Если хорда меньше, то расстояние от центра окружности до этой хорды больше. Верно и обратное Наибольшая возможная хорда является диаметром Серединный перпендикуляр к хорде проходит через центр окружности Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр перпендикулярен этой хорде. Верно и обратное — если диаметр перпендикулярен хорде, то этот диаметр делит эту хорду пополам Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр делит дуги, стягиваемые этой хордой, пополам. Верно и обратное — если диаметр делит дугу пополам, то этот диаметр делит пополам хорду, стягивающую эту дугу Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус перпендикулярен этой хорде. Верно и обратное — если радиус перпендикулярен хорде, то этот радиус делит эту хорду пополам Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Верно и обратное — если радиус делит дугу пополам, то этот радиус делит пополам хорду, стягивающую эту дугу. Если радиус перпендикулярен хорде, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Верно и обратное — если радиус делит дугу пополам, то этот радиус перпендикулярен хорде, стягивающей эту дугу. Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать Свойства хорды и вписанного угла Видео:Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать Свойства хорды и центрального угла Видео:Радиус описанной окружностиСкачать Формулы нахождения хорды Обозначения в формулах: l — длина хорды α — величина центрального угла R — радиус окружности d — длина перпендикуляра, проведенного от центра окружности к хорде Длина хорды окружности равна удвоенному радиусу данной окружности, умноженному на синус половины центрального угла. Сумма квадрата половины длины хорды и квадрата перпендикуляра, проведенного к этой хорде, равна квадрату радиуса окружности. Данная формула следует из теоремы Пифагора. Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать Решение задач Примечание. Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен. Задача. Хорды АВ и СD пересекаются в точке S, при чем AS:SB = 2:3, DS = 12см, SC = 5см, найти АВ. Решение. Поскольку соотношение AS:SB = 2:3 , то пусть длина AS = 2x, SB = 3x Согласно свойству хорд AS x SB = CS x SD, тогда 2х * 3х = 5 * 12 6х 2 = 60 х 2 = 10 x = √10 Откуда AB = AS + SB AB = 2√10 + 3√10= 5√10 Окружность разделена на части, которые относятся как 3,5:5,5:3 и точки деления соединены между собой. Определить величину углов образовавшегося треугольника. Решение. Обозначим коэффициент пропорциональности дуг окружности, как х. Соединим центры окружности с концами дуг. Поскольку центральный угол равен градусной мере дуги, на которую опирается, то соотношение центральных углов окружности будет равно соотношению ее частей (дуг). Поскольку градусная мера окружности равна 360 градусам, то 3,5х + 5,5х + 3х = 360 12х = 360 х = 30 Откуда градусные величины центральных углов равны: 3 * 30 = 90 3,5 *30 = 105 5,5 *30 = 165 Углы образовавшегося треугольника являются углами, вписанными в окружность. Вписанный угол равен половине градусной меры дуги, на которую опирается. Откуда углы треугольника равны: 90 / 2 = 45 105 / 2 = 52,5 165 / 2 = 82,5 Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ; 📽️ Видео ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать Вписанная и описанная окружности | Лайфхак для запоминанияСкачать Окружность. Длина хорды. Теорема синусов.Скачать ОГЭ ЗАДАНИЕ 16 НАЙДИТЕ ДЛИНУ ХОРДЫ ОКРУЖНОСТИ ЕСЛИ РАДИУС 13 РАССТОЯНИЕ ДО ХОРДЫ 5Скачать ищем хорду в окружности. огэ 1 часть геометрияСкачать Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать Равносторонний треугольник и три хорды в описанной окружностиСкачать Сможешь найти радиус окружности? Окружность, вписанная в прямоугольный треугольникСкачать Поделиться или сохранить к себе: Смотрите также Ящик тянут по земле по горизонтальной окружности длиной 60 Ящик тянут по земле по горизонтальной окружности длиной 40 Ящик тянут по земле по горизонтальной окружности диаметром 20 Ящик тянут по земле за веревку по горизонтальной окружности длиной Ящик тянут по земле за веревку по горизонтальной окружности диаметром Электрон равномерно движется по окружности в однородном магнитном поле Электрон и протон ускоренные разностью потенциалов движутся по окружности Шарик скатывается по желобу изогнутому в виде дуги окружности