Высота пирамиды основание треугольник

В этом уроке приведены определение и свойства правильной треугольной пирамиды и ее частного случая — тетраэдра (см. ниже). Ссылки на примеры решения задач приведены в конце урока.

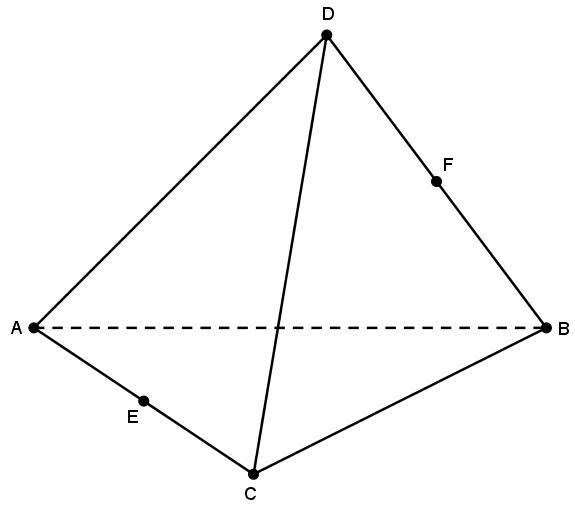
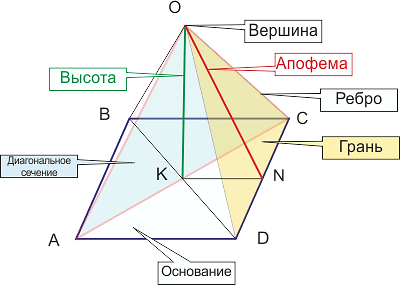
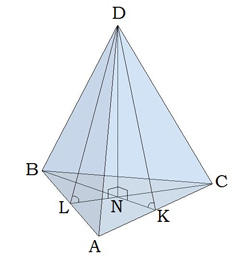
Видео:Как найти высоту пирамиды. Начертательная геометрияСкачать

Определение

Правильная треугольная пирамида — это пирамида, основанием которой является правильный треугольник, а вершина проецируется в центр основания.

На рисунке обозначены:
ABC — Основание пирамиды
OS — Высота
KS — Апофема
OK — радиус окружности, вписанной в основание
AO — радиус окружности, описанной вокруг основания правильной треугольной пирамиды
SKO — двугранный угол между основанием и гранью пирамиды (в правильной пирамиде они равны)

Важно. В правильной треугольной пирамиде длина ребра (на рисунке AS, BS, CS ) может быть не равна длине стороны основания (на рисунке AB, AC, BC). Если длина ребра правильной треугольной пирамиды равна длине стороны основания, то такая пирамида называется тетраэдром (см. ниже).

Видео:№251. Основанием пирамиды DABC является прямоугольный треугольник с гипотенузой ВС. БоковыеСкачать

Свойства правильной треугольной пирамиды:

• боковые ребра правильной пирамиды равны
• все боковые грани правильной пирамиды являются равнобедренными треугольниками
• в правильную треугольную пирамиду можно как вписать, так и описать вокруг неё сферу
• если центры вписанной и описанной вокруг правильной треугольной пирамиды, сферы совпадают, то сумма плоских углов при вершине пирамиды равна π (180 градусов) , а каждый из них соответственно равен π / 3 (пи делить на 3 или 60 градусов ).
• площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему
• вершина пирамиды проецируется на основание в центр правильного равностороннего треугольника,, который является центром вписанной окружности и точкой пересечения медиан

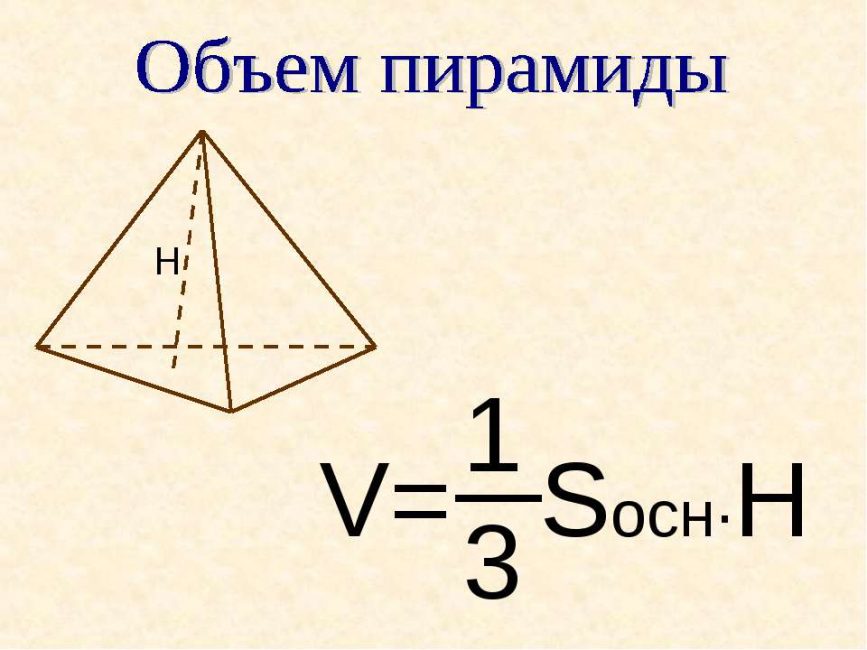
Формулы для правильной треугольной пирамиды

Формула объема правильной треугольной пирамиды:

V — объем правильной пирамиды, имеющей в основании правильный (равносторонний) треугольник
h — высота пирамиды
a — длина стороны основания пирамиды
R — радиус описанной окружности
r — радиус вписанной окружности

Поскольку правильная треугольная пирамида является частным случаем правильной пирамиды, то формулы, которые верны для правильной пирамиды, верны и для правильной треугольной — см. формулы для правильной пирамиды.

Примеры решения задач:

Видео:Построение проекции пирамиды. Метод прямого треугольника.Скачать

Тетраэдр

Частным случаем правильной треугольной пирамиды является тетраэдр.

Тетраэдр — это правильный многогранник (правильная треугольная пирамида) у которой все грани являются правильными треугольниками.

• Все грани равны
• 4 грани, 4 вершины и 6 ребер
• Все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны

Медиана тетраэдра — это отрезок, соединяющий вершину с точкой пересечения медиан противоположной грани (медиан равностороннего треугольника, противолежащего вершине)

Бимедиана тетраэдра — это отрезок, соединяющий середины скрещивающихся рёбер (соединяющий середины сторон треугольника, являющегося одной из граней тетраэдра)

Высота тетраэдра — это отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани (то есть является высотой, проведенной от любой грани, также совпадает с центром описанной окружности).

Тетраэдр обладает следующими свойствами:

• Все медианы и бимедианы тетраэдра пересекаются в одной точке
• Эта точка делит медианы в отношении 3:1, считая от вершины
• Эта точка делит бимедианы пополам

Видео:№260. Высота, проведенная к основанию равнобедренного треугольника, равна 7,6 см, а боковая сторонаСкачать

Формулы и свойства правильной треугольной пирамиды. Усеченная треугольная пирамида

Объемной фигурой, которая часто появляется в геометрических задачах, является пирамида. Самая простая из всех фигур этого класса — треугольная. В данной статье разберем подробно основные формулы и свойства правильной пирамиды треугольной.

Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Геометрические представления о фигуре

Прежде чем переходить к рассмотрению свойств правильной пирамиды треугольной, разберемся подробнее, о какой фигуре идет речь.

Предположим, что имеется произвольный треугольник в трехмерном пространстве. Выберем в этом пространстве любую точку, которая в плоскости треугольника не лежит, и соединим ее с тремя вершинами треугольника. Мы получили треугольную пирамиду.

Вам будет интересно: Лихой — это: значение и синонимы

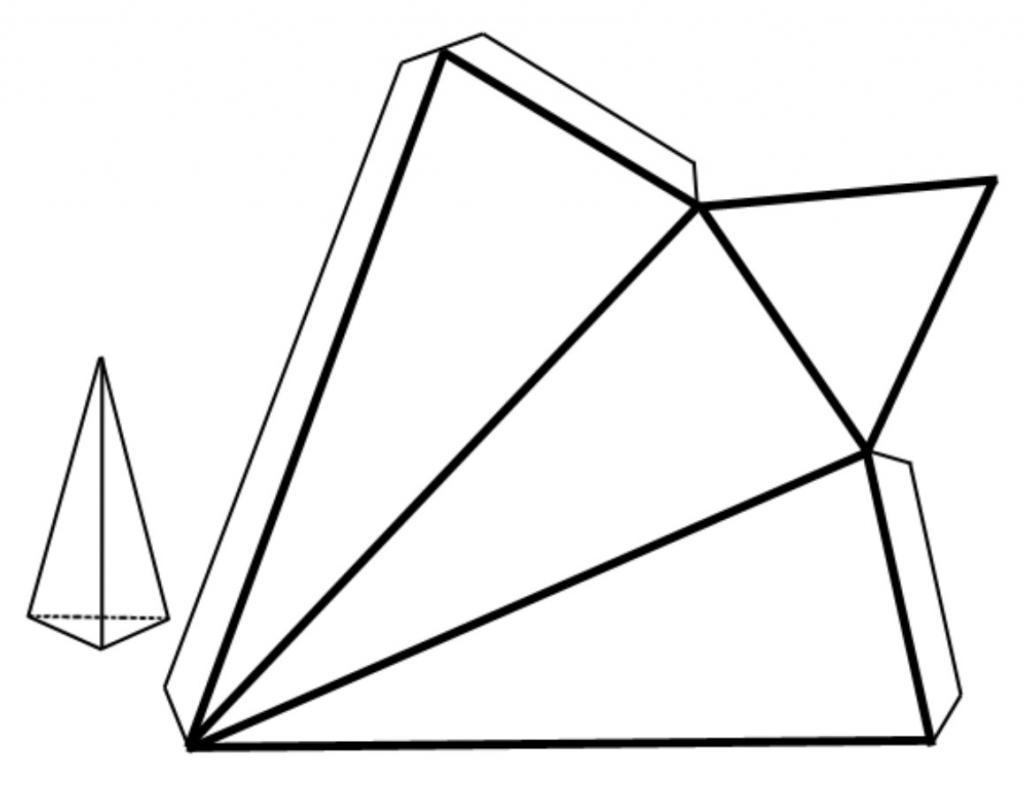
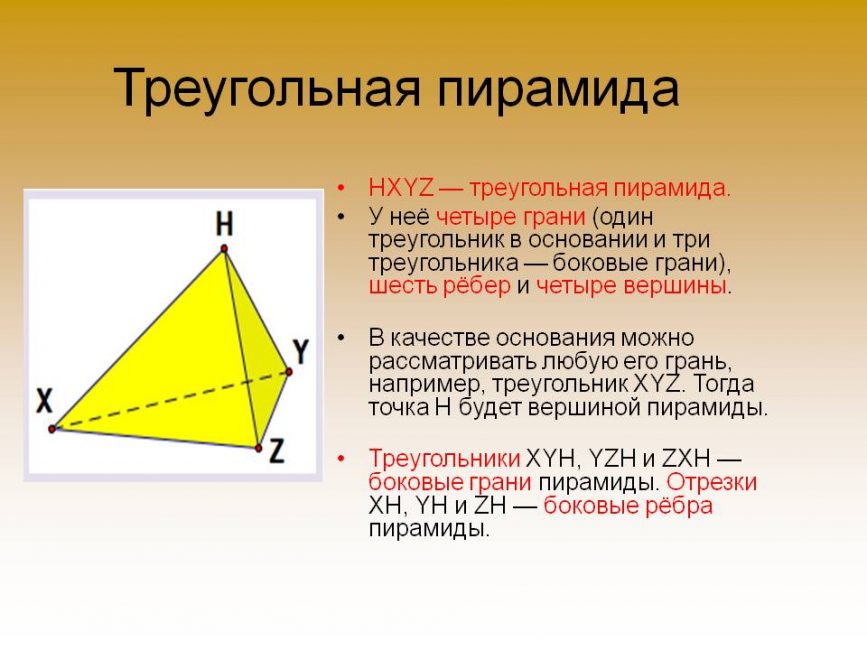
Она состоит из 4-х сторон, причем все они являются треугольниками. Точки, в которых соединяются три грани, называются вершинами. Их у фигуры также четыре. Линии пересечения двух граней — это ребра. Ребер у рассматриваемой пирамиды 6. Рисунок ниже демонстрирует пример этой фигуры.

Поскольку фигура образована четырьмя сторонами, ее также называют тетраэдром.

Видео:№252. Основанием пирамиды DABC является равнобедренный треугольник ABC, в котором АВ = АС, ВС=6 смСкачать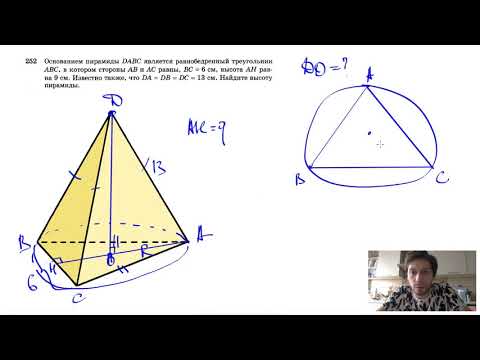

Правильная пирамида

Выше была рассмотрена произвольная фигура с треугольным основанием. Теперь предположим, что мы провели перпендикулярный отрезок из вершины пирамиды к ее основанию. Этот отрезок называется высотой. Очевидно, что можно провести 4 разные высоты для фигуры. Если высота пересекает в геометрическом центре треугольное основание, то такая пирамида называется прямой.

Прямая пирамида, основанием которой будет треугольник равносторонний, называется правильной. Для нее все три треугольника, образующих боковую поверхность фигуры, являются равнобедренными и равны друг другу. Частным случаем правильной пирамиды является ситуация, когда все четыре стороны являются равносторонними одинаковыми треугольниками.

Рассмотрим свойства правильной пирамиды треугольной и приведем соответствующие формулы для вычисления ее параметров.

Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Сторона основания, высота, боковое ребро и апотема

Любые два из перечисленных параметров однозначно определяют остальные две характеристики. Приведем формулы, которые связывают названные величины.

Предположим, что сторона основания треугольной пирамиды правильной равна a. Длина ее бокового ребра равна b. Чему будут равны высота правильной пирамиды треугольной и ее апотема.

Для высоты h получаем выражение:

Эта формула следует из теоремы Пифагора для прямоугольного треугольника, сторонами которого являются боковое ребро, высота и 2/3 высоты основания.

Апотемой пирамиды называется высота для любого бокового треугольника. Длина апотемы ab равна:

Из этих формул видно, что какими бы ни были сторона основания пирамиды треугольной правильной и длина ее бокового ребра, апотема всегда будет больше высоты пирамиды.

Представленные две формулы содержат все четыре линейные характеристики рассматриваемой фигуры. Поэтому по известным двум из них можно найти остальные, решая систему из записанных равенств.

Видео:Пирамиды, в которых высота проходит через центр описанной около основания окружностиСкачать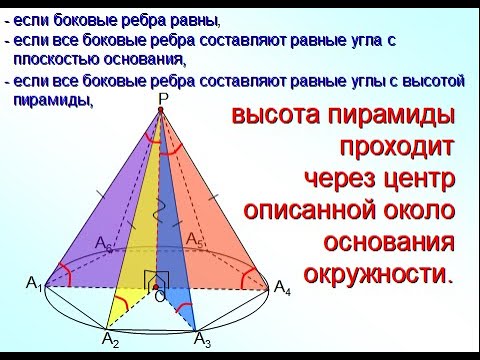

Объем фигуры

Для абсолютно любой пирамиды (в том числе наклонной) значение объема пространства, ограниченного ею, можно определить, зная высоту фигуры и площадь ее основания. Соответствующая формула имеет вид:

Применяя это выражение для рассматриваемой фигуры, получим следующую формулу:

Где высота правильной треугольной пирамиды равна h, а ее сторона основания — a.

Не сложно получить формулу для объема тетраэдра, у которого все стороны равны между собой и представляют равносторонние треугольники. В таком случае объем фигуры определится по формуле:

То есть он определяется длиной стороны a однозначно.

Видео:№246. Высота треугольной пирамиды равна 40 см, а высота каждой боковой грани, проведеннаяСкачать

Площадь поверхности

Продолжим рассматривать свойства пирамиды треугольной правильной. Общая площадь всех граней фигуры называется площадью ее поверхности. Последнюю удобно изучать, рассматривая соответствующую развертку. На рисунке ниже показано, как выглядит развертка правильной пирамиды треугольной.

Предположим, что нам известны высота h и сторона основания a фигуры. Тогда площадь ее основания будет равна:

Получить это выражение может каждый школьник, если вспомнит, как находить площадь треугольника, а также учтет, что высота равностороннего треугольника также является биссектрисой и медианой.

Площадь боковой поверхности, образованной тремя одинаковыми равнобедренными треугольниками, составляет:

Данное равенство следует из выражения апотемы пирамиды через высоту и длину основания.

Полная площадь поверхности фигуры равна:

S = So + Sb = √3/4*a2 + 3/2*√(a2/12+h2)*a

Заметим, что для тетраэдра, у которого все четыре стороны являются одинаковыми равносторонними треугольниками, площадь S будет равна:

Видео:🔴 Найдите объём правильной четырёхугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Свойства правильной усеченной пирамиды треугольной

Если у рассмотренной треугольной пирамиды плоскостью, параллельной основанию, срезать верх, то оставшаяся нижняя часть будет называться усеченной пирамидой.

В случае правильной пирамиды с треугольным основанием в результате описанного метода сечения получается новый треугольник, который также является равносторонним, но имеет меньшую длину стороны, чем сторона основания. Усеченная треугольная пирамида показана ниже.

Мы видим, что эта фигура уже ограничена двумя треугольными основаниями и тремя равнобедренными трапециями.

Предположим, что высота полученной фигуры равна h, длины сторон нижнего и верхнего оснований составляют a1 и a2 соответственно, а апотема (высота трапеции) равна ab. Тогда площадь поверхности усеченной пирамиды можно вычислить по формуле:

S = 3/2*(a1+a2)*ab + √3/4*(a12 + a22)

Здесь первое слагаемое — это площадь боковой поверхности, второе слагаемое — площадь треугольных оснований.

Объем фигуры рассчитывается следующим образом:

V = √3/12*h*(a12 + a22 + a1*a2)

Для однозначного определения характеристик усеченной пирамиды необходимо знать три ее параметра, что демонстрируют приведенные формулы.

Видео:№240. Основанием пирамиды является параллелограмм, стороны которого равны 20 см и 36 см,Скачать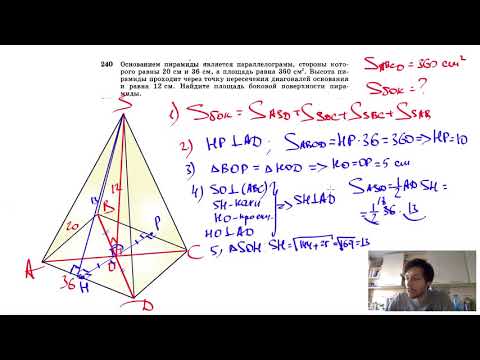

Как найти высоту в пирамиде: треугольной, четырехугольной, правильной

Высота основания в пирамиде – тема, на которую часто попадаются задачи на экзаменах и в старших классах. Решать такие задачи просто, если понимать принцип решения и знать формулы.

В нашей статье, вы без лишних формул и теории сможете понять, как решать задачи на нахождение высоты в пирамиде. Обратите внимание, что в разделе «формулы» отсутствуют все формулы правильной пирамиды, так как наша цель – научить решать задачи на нахождение высоты.

Содержание этой статьи:

Видео:№250. Основанием пирамиды является равнобедренный треугольник с углом 120°. Боковые ребраСкачать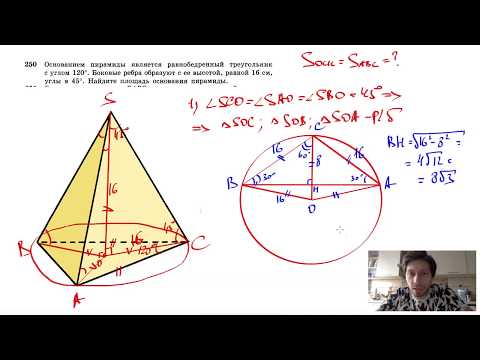

Теория

Правильная пирамида

Правильная пирамида имеет в основании многоугольник, а высота проходит через центр основания. Боковые грани – равнобедренные треугольники. Напомним, что в равнобедренном треугольнике две стороны равны, следовательно, боковые ребра в правильной пирамиде тоже равны. Многоугольник в основании правильный, т.е. его стороны равны.

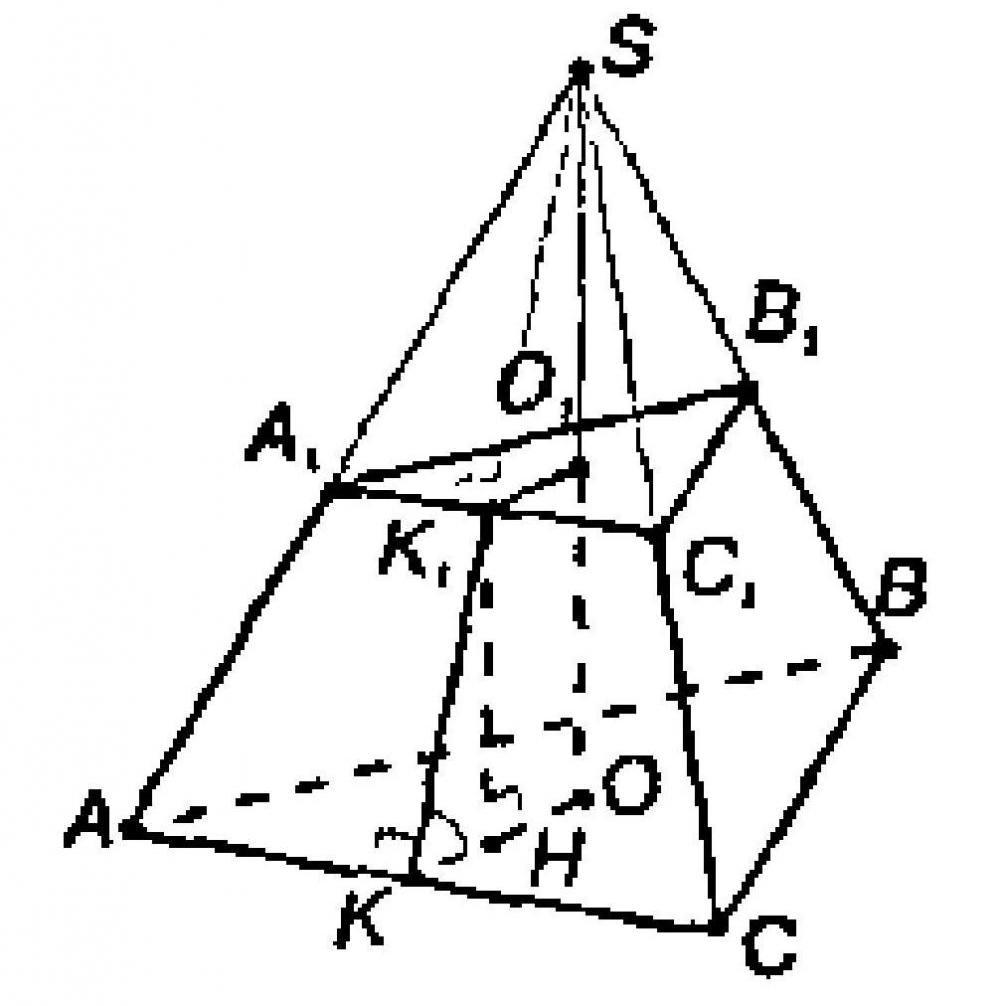
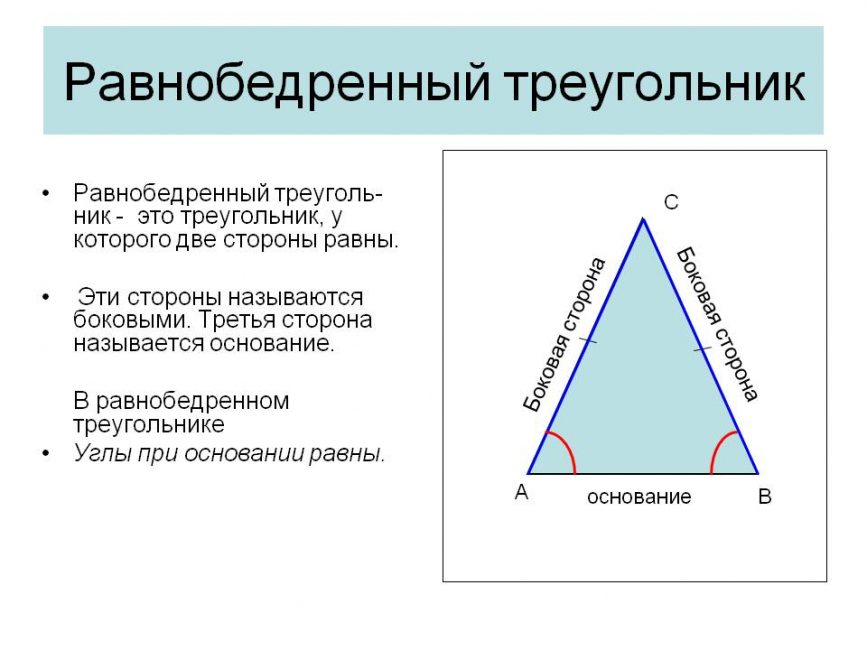
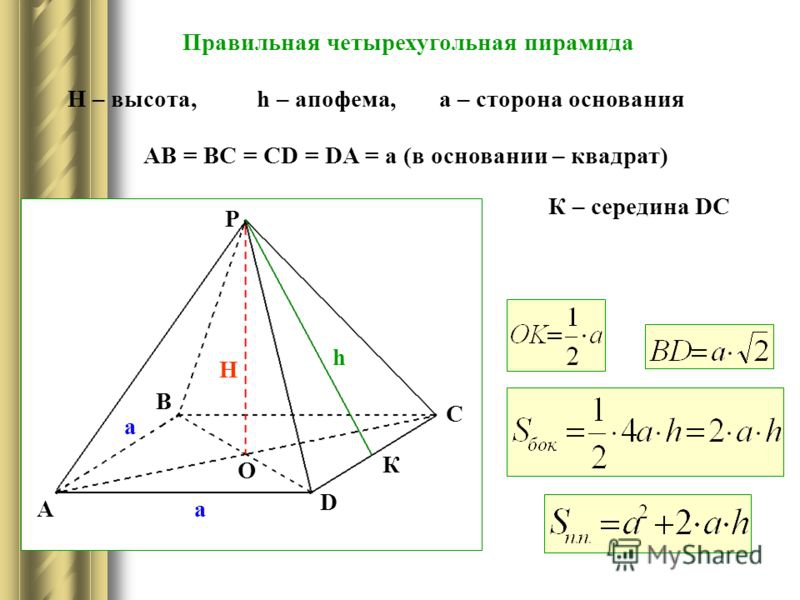
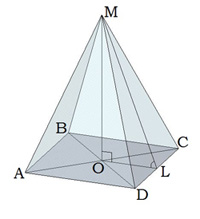
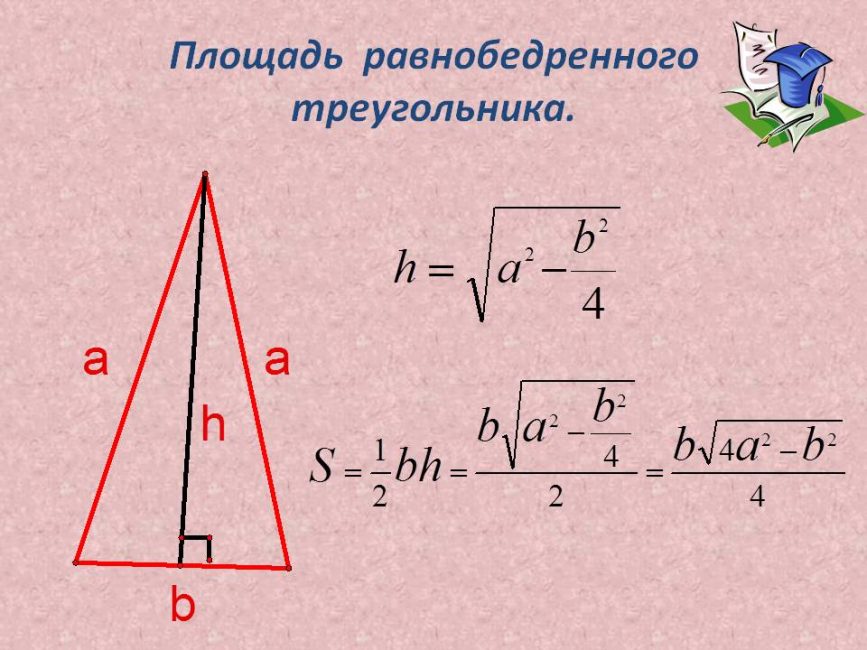
Для решения задач понадобится знать теоремы равнобедренного треугольника:

Основные свойства

Четырехугольная пирамида

В основании – многоугольник; остальные грани – треугольники, соединяющиеся в общей вершине.

Треугольная пирамида

В качестве основания можно рассматривать любую грань. Вся фигура состоит из треугольников.

Необходимые знания для нахождения высоты

Когда теория закреплена, можно переходить к формулам.

Формулы для нахождения высоты

Запомните, что маленькая буква h – это апофема, а большая H – высота.

В некоторых задачах, высоту можно найти через объем:

ВИДЕО: Примеры решения задач

Нахождение высоты в правильной пирамиде

Нахождение высоты в правильной пирамиде

Ниже будут представлены текстовые решения часто встречающихся задач.

Треугольная пирамида

Задача 1

В правильной треугольной пирамиде DBAC с вершиной D биссектрисы треугольника BAC пересекаются в точке N. Площадь треугольника BAC равна 4; объем пирамиды равен 12. Найдите длину отрезка DN.

DN – высота, следовательно, объем фигуры можно выразить по формуле:

DN = 3V/S основания = 3*12/4 = 9

Задача 2

DBAC – медианы основания BAC. Они пересекаются в точке N. Площадь ΔBAC равна 18, V = 20; найдите высоту.

Пользуясь формулой объема, получается:

DN = 3V/S ΔBAC = 3*36/18 = 108/18 = 6

Четырехугольная пирамида

Задача 1

Найдите высоту пирамиды, если ML = 10, а DC = 12. В основании квадрат.

ML – это апофема, сторона нам известна, следовательно, можно применить формулу для нахождения OL:

Известно, что MOL – прямоугольный угол. Применим теорему Пифагора:

MO ² = √ML ² — √OL ² = √100- √36 = √64

Задача 2

Известно, что диагональ AC = 20, ML = 10, а сторона DC = 12; найдите MO правильной четырехугольной пирамиды.

Найдем OL

В основании фигуры – квадрат, стороны и углы которого равны. Значит, половина диагонали = 10. Рассмотрим треугольник LOC, он – прямоугольный. Из исходных данный ясно, что LC = 6 (в равнобедренном треугольнике, высота, проведенная из вершины, делит основание на 2 равные части – это свойство р/б треугольника).

Пользуясь теоремой Пифагора, находим OL:

OL² = √OC² — √LC² = √100 – √36 = √64 = 8

Задача 3

Ищем MO

Пользуясь той же теоремой, находим высоту:

MO² = √ML² – √OL² = 100 – 64 = 36

Задача 4

Известно, что в основании ABCD, AB=CD=BC=AD. Треугольник DMC имеет площадь 36см, DC = 4, OL = 6. Определите тип фигуры и найдите высоту.

Исходя из информации про основание, мы сделали вывод, что перед нами правильная пирамида – стороны основания равны. Следовательно, перед нами четырехугольная правильная пирамида.

Из первого вывода следует, что боковые грани – равнобедренные треугольники, а высота и медиана этих треугольников – апофема. Пользуясь формулами, найдем высоту.

Площадь равнобедренного треугольника

Теперь у нас есть апофема, а OL нам было уже давно. MOL – прямоугольный треугольник, 2 стороны которого, мы уже знаем. Следовательно, мы можем посчитать высоту.

MO = ML – OL = 18 – 6 = 12

Видео:№243. Основанием пирамиды DABC является треугольник ABC, у которого АВ = АС= 13 см, ВС=10 см; реброСкачать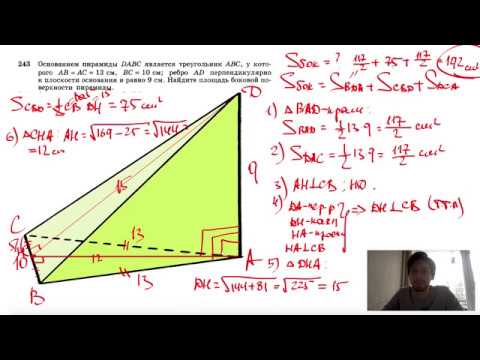

Часто задаваемые вопросы

Часто в задании не указывают какой тип фигуры, чтобы человек сам догадался и применил нужные формулы. Понять какой тип фигуры легко – начните решение задачи с рассмотрения основания и заучивания свойств фигуры.

Зная определения и свойства, определить тип фигуры очень легко.

Чтобы решать задачи, человек должен включать логику, а не подставлять исходные числа в знакомые формулы. С этим расчетом, в некоторых задачах умышленно добавляют лишние данные, которые могут даже не использоваться при решении. Чаще такое встречается в задачах на ЕГЭ.

Для удобства, человек может не выделять отдельно высоту, а сразу писать, например, BE (если B – вершина, а E – основание). То же с апофемой. Важно, чтобы сам человек осознавал, что это за линия и как ее использовать в решении.

Ключ к пониманию стереометрии – умение визуализировать объекты в пространстве. Если в дополнение к этому умению, знать формулы, свойства и теорию – задачи будут решаться быстро и безошибочно.

Если выразить высоту через формулу объема, то получится следующее:

Пример: объем пирамиды равен 70 куб. см., а площадь боковых граней – 30см²

Видео:Начертательная геометрияСкачать

Типичные ошибки на ЕГЭ

Видео:Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

Полезные советы

• Если в задаче указан объем – ищите высоту через него.
• Делите равнобедренные треугольники на прямоугольные – так быстрее и проще решить задачу.
• Учите квадратные корни чисел – так, вы будете быстрее справляться с теоремой Пифагора.
• Не кидайтесь сразу к решению – изучите исходные данные и сделайте правильные выводы.
• Если в заданиях получаются слишком крупные числа (от 1000), то перепроверьте решение – вероятно, вы допустили ошибку. В заданиях в учебнике и на экзамене практически не используются крупные числа.

Чтобы успешно решить задачу для нахождения высоты пирамиды, достаточно знать теорию и формулы. Добавив к своим знаниям немного практики и внимательности, вы легко и быстро будете решать подобные задачи! Если вы не согласны с рейтингом статьи, то просто поставьте свои оценки и аргументируйте их в комментариях. Ваше мнение очень важно для наших читателей. Спасибо!

🎬 Видео

Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать

Как Фалес Милетский измерял высоту пирамидыСкачать

КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать

Вычисляем высоту через координаты вершин 1Скачать

Делаем модель пирамиды для решения задачи по стереометрииСкачать