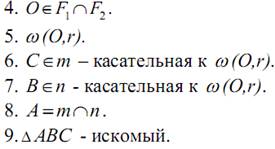Как найти гмт треугольника (4 видео) | Курс школьной геометрии

Геометрические места точек

Геометрическим местом точек называют множество точек, заданное условием, являющимся и свойством, и признаком.

Другими словами, все точки из рассматриваемого геометрического места точек, и только они, удовлетворяют заданному условию.

Примеры геометрических мест точек (сокращённо ГМТ ) на плоскости представлены в следующей таблице, причём геометрические места точек изображаются в таблице красным цветом .

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Примеры решения задач, решаемых методом ГМТ

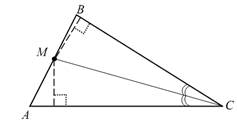
Задача 1. На стороне треугольника найти точку, равноотстоящую от двух

других сторон треугольника.

Анализ. Пусть задача решена и точка М на стороне АВ находится на

одинаковом расстоянии от сторон АС и ВС, образующих угол С.

Так как все точки, равноудаленные от сторон угла С лежат на биссектрисе этого угла (гмт 5), то точка М удовлетворяет двум независимым условиям:

Доказательство. Легко видеть, что точка М удовлетворяет требованиям

Задача 2. Построить треугольник по основанию а, углу при вершине А

Анализ. Допустим, что задача решена и искомый треугольник ΔАВС

построен так, что BC = a, AM = m_а – медиана и ∟ВАС = α.

Отрезок ВС, равный данному, всегда может быть построен. Тогда задача сводится к построению точки А, удовлетворяющей двум независимым условиям:

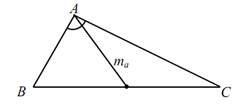
1 0 . Точка А находится на расстоянии m_а от середины М стороны ВС, т.е.

2 0 . Так как ∟ВАС = α, то точка А принадлежит ГМТ F1, из которых отрезок ВС виден под углом α, т.е.

Таким образом,

Заданные по условию задачи элементы могут быть выбраны перед построением или анализом.

Доказательство: BC = a, AM = m_а по построению, и ∟СВО = 90 0 – α, следовательно, ∟ВОМ = α, следовательно, ∟ВОС=2α, а ∟ВАС =0,5*∟ВОС= α

и, следовательно ΔАВС, удовлетворяет всем условиям задачи и потому искомый.

Исследование: Задача имеет столько решений, сколько точек содержит

пересечение двух окружностей. Если пересечение в двух точках, то два

решения; в одной (окружности касаются) – одно решение, не пересекаются –нет решений.

Задача 3. Построить окружность данного радиуса r, проходящую через данную точку М и высекающую на данной прямой l отрезок длины d, равный данному.

Анализ: Пусть искомая окружность построена. Пусть О – ее центр, r – данный радиус, М – данная точка, АВ – хорда длины d, построенной окружности, лежащей на данной прямой l. Опустим перпендикуляр ОC на прямую l. В прямоугольном треугольнике ОВС известна гипотенуза (данный радиус r) и катет ВС, равный половине данного отрезка. Кроме того, ОМ = r.

Значит, искомый центр О принадлежит, во-первых ГМТ F1, удаленных от данной прямой l на расстояние, равное ОС(ГМТ 3); во-вторых ГМТ F2, удаленных от данной точки М на расстояние, равное данному радиусу r (гмт2).

Окружность ω может быть построена, ГМТ F1 может быть построено, если мы найдем расстояние OC = h.

Для этого построим вспомогательный треугольник О₁В₁С₁ по гипотенузе О₁В₁ = r и катету В₁С₁ = d/2. Тогда h = O₁C₁ будет найден.

Построение:

Доказательство: Убеждаемся в том, что построенная окружность удовлетворяет всем требованиям задачи. OM = r по построению. Докажем, что AB = d.

Действительно, ΔАОВ — равнобедренный (ОС –

медиана и высота), отсюда АВ = 2ВС = 2*d/2 = d.

Исследование: Построение 1 возможно, если d 0 ) точки О можно отметить сразу – она находится на расстоянии r от стороны ВС, то есть центр О вписанной окружности принадлежит ГМТ, находящихся на расстоянии r от прямой ВС (ГМТ 3). (Как правило, мы строим только в одной из двух полуплоскостей, определяемых заданной прямой). Второе свойство, которым обладает точка О, видно не сразу. Но, исходя из свойств вписанной окружности, это свойство мы можем найти: центр вписанной окружности находится на пересечении биссектрис треугольника и потому ОВ и ОС – биссектрисы углов В и С.

Тогда: ∟ВОС = 180 0 – 0,5(∟В + ∟С) = 180 0 – 0,5 (180 0 — ∟А) = 90 0 + 0,5∟А

Так как ∟ВОС =90 0 +∟A/2, то точка О принадлежит ГМТ F2, из которых

данный отрезок ВС виден под данным углом α = 90 0 + ∟А/2 (ГМТ 6). ГМТ F1 и F2 может быть построено, а потому и точка может быть построена и мы можем перейти к построению искомой фигуры.

Доказательство: Убеждаемся в том, что построенный треугольник

удовлетворяет всем требованиям задачи. ВС = а, окружность ω(O,r) вписана в

треугольник по построению. Остается доказать, что ∟ВАС равен данному углу

А. Действительно, по построению ∟О₁ ВК = ∟А/2. Тогда

Теперь находим:

Значит, ΔАВС удовлетворяет всем условиям задачи, а потому – искомый.

Исследование. Построения 1-3 выполняются и притом однозначно при

любых a, r и ∟ A 0 . Построение 4 возможно лишь тогда, когда прямая F1

пересекает окружность F2, то есть при условии или при: (*). При этом прямая F1 пересекает окружность F2 в

двух или одной точке соответственно. Построения 6 и 7 всегда выполнимы, так

как из любой точки вне окружности можно провести к ней две касательные

(одна из них в данном случае прямая ВС). А вот построение 8 возможно не всегда: прямые m и n могут быть параллельными или могут пересекаться в полуплоскости, не содержащей точку О. В этих случаях в нужной нам полуплоскости точка А не строится. Вывод: при выполнении условий ∟A 0 и (*) задача может иметь одно, два или ни одного решения.

4. Построение Штейнера и построение с помощью
двусторонней линейки, прямого или острого угла [2], [5]

Якоб Штейнер (18.05 1795г. – 01.04.1863г.) сын простых поселян из Уцисдорфа Германии. Как он сам писал: «Только на девятнадцатом году стремление к образованию стало для меня потребностью…. и с осени 1822г. Вынужден с величайшим трудом добывать средства к существованию частными уроками. Почти бессознательно я пришел таким образом к собственно геометрическому способу рассмотренья, как оно должно быть присуще геметрии древности, но я находился в случае, противоположном им. Мне было дано множество разрешимых задач и предложений, и мне приходилось заняться не фиксацией отдельных предложений, а установлением того свойства общих законов систематического построения, что из них вытекают все открытия подобного рода, и их соответственным образом исчерпать».

«Геометрия в более тесном смысле для своих построений нуждается только в двух инструментах, циркуле и линейке. …. все построения могут быть выполнены только при помощи линейки, если где-либо в дан будет вспомогательный неподвижный круг»

Рассмотрим решение задач проведением только одних прямых линий, причём на чертеже иногда уже имеется начерченной какая-нибудь одна вспомогательная фигура. Из всех таких способов наиболее сильными являются решения с помощью:

1. Двусторонней линейки, другие инструменты при этом не допускаются

2. Прямого или острого угла, сделанного из дерева или металла — другие инструменты не допускаются.

3. Односторонней линейки, причём на чертеже уже имеется начерченной окружность с известным центром.

Далее, всякая не вспомогательная окружность считается данной, если известно положение ее центра и длина радиуса, заданная где-нибудь начерченным отрезком. Однако ни одна точка такой окружности точку какого-нибудь свойства, то должны ограничиться проведением только прямых линий.

Мы знаем, что решение квадратной задачи сводится к известным четырём основным построениям.

Из этих основных задач первая и третья решаются способами 1, 2 и 3

непосредственно — одной линейкой. Моя цель показать, что две другие основные задачи решаются теми же тремя способами, которые решают теми же способами всякую квадратную задачу.

Решим несколько задач проведением одних прямых линий (односторонней линейкой).

Найти геометрическое место центров окружностей, проходящих через две данные точки.

Пусть окружность с центром O проходит через данные точки A и B. Поскольку OA = OB (как радиусы одной окружности), точка O лежит на серединном перпендикуляре к отрезку AB. Обратно, каждая точка O, лежащая на серединном перпендикуляре к AB, равноудалена от точек A и B. Значит, точка O — центр окружности, проходящей через точки A и B.

Проведем диаметры АА1, ВВ1, затем хорды АВ1, ВА1, эти последние перпендикулярны АВ и потому параллельны между собой. Поэтому для решения задачи нужно провести через точку О прямую, параллельную эти хордам. Она будет серединным перпендикуляром к АВ, т.е. искомым ГМТ [5, стр.21]

Дан прямоугольник ABCD. Найдите ГМТ X, для которых AX + BX = CX + DX.

Пусть l — прямая, проходящая через середины сторон BC и AD.

Предположим, что точка X не лежит на прямой l, например, что точки A и X лежат по одну сторону от прямой l. Тогда AX

Видео:PRO геометрические места точекСкачать

Геометрическое место точек

Геометрическое место точек (ГМТ) — это фигура, состоящая из всех точек плоскости, удовлетворяющих определённому условию.

Чтобы выяснить, что собой представляет некоторая фигура F — геометрическое место точек, удовлетворяющих заданному условию P, нужно доказать:

1) если определённая точка принадлежит фигуре F, то она удовлетворяет заданному условию P;

2) если определённая точка удовлетворяет заданному условию P, то она принадлежит фигуре F.

(то есть требуется доказать прямую теорему — свойство P точек, принадлежащих фигуре F, и обратную теорему — признак фигуры F: если точка удовлетворяет условию P, то она принадлежит F).

Геометрическое место точек, равноудалённых от данной точки — окружность.

Это следует непосредственно из определения окружности.

Некоторые теоремы о ГМТ

1) Геометрическим местом точек, равноудалённых от двух данных точек, является серединный перпендикуляр к отрезку, соединяющему эти точки.

2) Геометрическим местом точек, равноудалённых от сторон неразвёрнутого угла, является биссектриса этого угла.

3) Геометрическим местом точек, удалённых от данной прямой на расстояние h, состоит из двух прямых, параллельных данной прямой и отстоящих от неё на h.

4) Геометрическим местом точек, равноудалённых от двух параллельных прямых, является прямая, параллельная этим прямым и проходящая через середину их общего перпендикуляра.

Понятие ГМТ часто используют при решении задач на построение.