Как найти длину вектора в r studio

Видео:Векторы (часть 1). Основы программирования на RСкачать

Понятие вектора в языке программирования R

Любой объект, который содержит данные называется data structure – структурой данных .

Вектор – это набор чисел, как правило, небольших размеров. Это – самый простой тип структуры данных в R. Даже одно число представляет собой вектор длиной в один элемент.

Вектор – поименованный одномерный объект, содержащий набор однотипных элементов.

Видео:Введение в R. Урок 4. Векторы в RСкачать

Создание векторов

Способ 1 – с()

Для создания векторов небольшой длины используется функция конкатенации c() (от «concatenate» – объединять, связывать).

В качестве аргументов этой функции через запятую перечисляют объединяемые в вектор значения. Например, зададим вектор z со значениями 1.1, 9, 3.14:

Способ 2 – scan()

Применяется функция scan(), которая «считывает» последовательно вводимые с клавиатуры значения. При этом выполнение команды scan завершают введением пустой строки

Заметьте, что X – заглавная буква. Если использовать прописную (х), то программа выдаст ошибку либо величину x , которая была ранее определена в листинге кода.

Этот способ требует внимательного ввода значений с клавиатуры. В случае, если вы введете другое, нежели требуется, число, необходимо будет либо вводить все значения заново, либо воспользоваться специальными инструментами для корректировки.

Способ 3 – seq()

При необходимости использования набора последовательных чисел, например, от 1 до 7, можно воспользоваться функцией seq()

Более того, функция seq() может устанавливать последовательность числе с шагом приращения:

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Операции над векторами

Векторы можно комбинировать, чтобы получить новый вектор.

Векторы можно объединять в один, как показано ниже

Векторы могут участвовать в арифметических операциях:

Каждый элемент вектора с именем my.vector1 сначала умножается на 2, а после к каждому из них прибавляется 100.

Другими распространенными арифметическими операциями являются

Чтобы найти квадратный корень можно использовать функцию

sqrt() или ^(1/2) , или ^0.5

Найдем корень вектора my.vector1 , элементы которого умножены на 2 и увеличены на 12.

Обратите внимание, что, когда программа выводит на экран ответ, в квадратных скобках указывается порядковый номер в наборе элементов.

Осуществим операцию деления над векторами:

Как видно, числа из меньшего вектора (2-го слагаемого) были добавлены к первым двум числам большего вектора (1-го слагаемого), а потом – к оставшимся двум числам в нем. Таким образом реализуется метод “Recycling” .

Можно проверить, есть ли элементы вектора меньше или больше некоторого значения, например:

Вектор может быть текстовым (character)

Если вы хотите объединить элементы текстового вектора в одну строку, то воспользуйтесь paste() , в котором аргумент collapse указывает программе, что между элементами должен быть один пробел.

Текстовые векторы тоже комбинируются. Допускается включение в вектор отдельных элементов

paste() может объединять элементы множества текстовых векторов. В самом простом случае объединяются два текстовых вектора, длина которых равняется 1, при этом аргумент sep отвечает за символ, стоящий между объединенными элементами

Если объединять текстовый вектор с числовым, программа преобразует все значения в текстовые:

Чтобы проверить, что new.vect является текстовым применим mode()

Далее объединим числовой и текстовый векторы одинаковой длины

Для векторов разной длины срабатывает “Recycling”

Чтобы обратится к конкретному элементу необходимо указать имя вектора и индекс этого элемента в квадратных скобках:

Из примера выше видно, что 4-й элемент вектора y равен 6. Ниже показано, что можно брать конкретные элементы из векторов и производить над ними операции:

Вывод нескольких последовательных значений , например, 2-го, 3-го и 4-го элементов вектора y , выполняется следующим образом

Чтобы выбрать конкретные элементы вектора, необходимо выполнить команду

Если при выводе требуется исключить некоторые элементы, то в предыдущей команде надо поставить минус «-»

Поддерживается также вывод по критерию. Например, выберем все значения больше 3

Благодаря индексам можно вносить исправления в вектор. Так, второй элемент вектора должен быть равным 4

Сортировка элементов вектора по возрастанию или убыванию осуществляется с помощью sort() . При этом аргументом, отвечающим за порядок сортировки, выступает decreasing , что означает «по убыванию» или «убывающий».

Еще раз о создании векторов. Помимо числовых и текстовых можно создавать логические векторы

Функция class() также используется для проверки типа вектора, при этом обратите внимание на результаты

Функция sum() вычисляет сумму элементов вектора

mean() – вычисляет среднее значение элементов вектора

Стандартное отклонение – sd()

Peter Dalgaard (2008). ‘Introductory Statistics with R’. Second Edition, Springer Science e+Business Media, LLC. 363 p.

Видео:Орт вектора. Нормировать вектор. Найти единичный векторСкачать

Визуализация и анализ географических данных на языке R

Структура данных — это программная единица, позволяющая хранить и обрабатывать множество однотипных и/или логически связанных данных. Структуры данных также являются типами данных, но не простыми, а составными. Поэтому обычно, когда говорят “тип данных”, подразумевают именно простые типы данных, рассмотренные в предыдущей главе. В R общеупотребительны следующие структуры данных: векторы, матрицы, массивы, фреймы данных, списки и факторы. С использованием структур данных тесно связаны циклы — разновидность управляющей конструкции, предназначенная для многократного повторения определенного набора инструкций.

Видео:R3 - Векторы в R. Часть 1Скачать

2.1 Однородные структуры данных

2.1.1 Векторы

Вектор представляет собой упорядоченную последовательность объектов одного типа. Вектор может состоять только из чисел, только из строк, только из дат или только из логических значений и т.д. Числовой вектор легко представить себе в виде набора цифр, выстроенных в ряд и пронумерованных согласно порядку их расстановки.

Вектор является простейшей и одновременно базовой структурой данных в R. Понимание принципов работы с векторами необходимо для дальнейшего знакомства с более сложными структурами данных, такими как матрицы, массивы, фреймы данных, тибблы, списки и факторы.

2.1.1.1 Создание

Существует множество способов создания векторов. Среди них наиболее употребительны:

1. Явное перечисление элементов
2. Создание пустого вектора (“болванки”), состоящего из заданного числа элементов
3. Генерация последовательности значений
4. Генерация случайного множества значений

Для создания вектора путем перечисления элементов используется функция c() :

Внимание: не используйте латинскую букву ‘c’ в качестве названия переменной! Это приведет к конфликту названия встроенной функции c() и определенной вами переменной

Помимо этого, распространены сценарии, когда вам нужно создать вектор, но заполнять его значениями вы будете по ходу выполнения программы — скажем, при последовательной обработке строк таблицы. В этом случае вам известно только предполагаемое количество элементов вектора и их тип. Здесь лучше всего подойдет создание пустого вектора, которое выполняется функцией vector() . Функция принимает 2 параметра:

• mode отвечает за тип данных и может принимать значения равные «logical» , «integer» , «numeric» (или «double» ), «complex» , «character» и «raw»
• length отвечает за количество элементов

Обратите внимание на то, что в первом случае подстановка параметров произведена в виде параметр = значение , а во втором указаны только значения. В данном примере оба способа эквивалентны. Однако первый способ безопаснее и понятнее. Если вы указываете только значения параметров, нужно помнить, что интерпретатор будет подставлять их именно в том порядке, в котором они перечислены в описании функции.

Описание функции можно посмотреть, набрав ее название в консоли ее название со знаком вопроса в качестве префикса. Например, для вышеуказанной функции надо набрать ?vector

Наконец, третий распространенный способ создания векторов — это генерация последовательности. Чтобы сформировать вектор из натуральных чисел от M до N , можно воспользоваться специальной конструкцией: M:N :

Существует и более общий способ создания последовательности — функция seq() , которая позволяет генерировать вектора значений нужной длины и/или с нужным шагом:

Как видно, параметры функции seq() можно комбинировать различными способами и указывать в произвольном порядке (при условии, что вы используете полную форму ( параметр = значение ). Главное, чтобы их совокупность однозначно описывала последовательность. Хотя, скажем, последний пример убывающей последовательности нельзя признать удачным с точки зрения наглядности.

Аналогичным образом можно создавать последовательности дат:

Часто оказывается полезным такая функция как генерация множества случайных значений, подчиненных определенному закону распределения. Наиболее часто испольщуются функции runif() (равномерное распределение) и rnorm() (нормальное распределение):

2.1.1.2 Индексирование

К отдельным элементам вектора можно обращаться по их индексам:

ВНИМАНИЕ: элементы векторов и других структур данных в языке R индексируются от 1 до N, где N — это длина вектора. Это отличает R от широко распространенных Си-подобных языков программирования (C, C++, C#, Java, Python), в которых индексы элементов начинаются с 0 и заканчиваются N-1. Например, первый элемент списка (аналог вектора в R) на языке Python извлекался бы как colors[0]. Будьте внимательны, особенно если программируете на нескольких языках.

Количество элементов (длину) вектора можно узнать с помощью функции length() :

Последний элемент вектора можно извлечь, если мы знаем его длину:

Последовательности удобно использовать для извлечения подвекторов. Предположим, нужно извлечь первые 4 элемента. Для этого запишем:

Индексирующий вектор можно создать заранее. Это удобно, если номера могут меняться в программе:

Обратите внимание на то что по сути один вектор используется для извлечения элементов из другого вектора. Это означает, что мы можем использовать не только простые последовательности натуральных чисел, но и векторы из прозвольных индексов. Например:

2.1.1.3 Преобразование

К числовым векторам можно применять множество функций. Прежде всего, нужно знать функции вычисления базовых параметров статистического ряда — минимум, максимум, среднее, медиана, дисперсия, размах вариации, среднеквадратическое отклонение, сумма:

Одной из мощнейших особенностей R является то что он не проводит различий между числами и векторами чисел. Поскольку R является матричным языком, каждое число представляется как вектор длиной 1 (или матрица (1х1) ). Это означает, что любая математическая функция, применимая к числу, будет применима и к вектору:

2.1.1.4 Поиск и сортировка

К важнейшим преобразованиям векторов относится их сортировка:

Другая распространенная задача — это поиск индекса элемента по его значению. Например, вы хотите узнать, какая ветка Московского метро (среди рассматриваемых) является самой длинной. Вы, конечно, легко найдете ее длину с помощью функции max(lengths) . Однако это не поможет вам узнать ее название, поскольку оно находится в другом векторе, и его индекс в массиве неизвестен. Поскольку векторы упорядочены одинаково, нам достаточно узнать, под каким индексом в массиве lengths располагается максимальный элемент, и затем извлечь цвет линии метро под тем же самым индексом. Дл поиска индекса элемента используется функция match() :

Здесь непохо бы лишний раз потренироваться в конкатенации строк, чтобы вывести результат красиво!

Ну и напоследок пример “матрешки”” из функций — как найти название самой плотной линии одним выражением:

2.1.1.5 Проверка условий

Проверка условия для вектора приводит к получению вектора логических значений:

Такого рода условия используются для фильтрации фреймов данных (см. далее)

Для векторов существует специальная форма векторизованного условного оператора – функция ifelse() . Она позволяет создать вектор, каждый элемент которого вычисляется по-разному в зависимости от значения элемента другого вектора в соответствующей позиции. Например, мы можем охарактеризовать каждую линию метро как длинную или короткую, установив порог в 20 км:

2.1.1.6 Описательные статистики

Можно получить краткую статистическую сводку по вектору (и любой другой структуре данных) с использованием функции summary() . Для качественных переменных выдаются частоты вхождения каждого случая, для количественных — набор основных описательных статистик:

2.1.2 Матрицы

Матрица — это обобщение понятия вектора на 2 измерения. С точки зрения анализа данных матрицы ближе к реальным данным, посколько каждая матрица по сути представляет собой таблицу со столбцами и строками. Однако матрица, как и вектор, может содержать только элементы одного типа (числовые, строковые, логические и т.д.). Позже мы познакомимся с фреймами данных, которые не обладают подобным ограничением.

Матрица, как правило, создается с помощью функции matrix , которая принимает 3 обязательных аргумента: вектор исходных значений, количество строк и количество столбцов:

По умолчанию матрица заполняется данными вектора по столбцам, что можно видеть в выводе программы. Если вы хотите заполнить ее по строкам, необходимо указать параметр byrow = TRUE :

Доступ к элементам матрицы осуществляется аналогично вектору, за исключением того что нужно указать положение ячейки в строке и столбце:

Помимо этого, из матрицы можно легко извлечь одну строку или один столбец. Для этого достаточно указать только номер строки или столбца, а номер второго измерения пропустить до или после запятой. Результат является вектором:

К матрицам можно применять операции, аналогичные операциям над векторами:

B и получать по ним описательные статистики:

А вот сортировка матрицы приведет к тому что будет возвращен обычный вектор:

К матрицам также применимы специальные функции, известные из линейной алгебры, такие как транспонирование и вычисление определителя:

Матрицы также можно перемножать с помощью специального оператора %*% . При этом, как мы помним, число столбцов в первой матрице должно равняться числу строк во второй:

Функция match() , которую мы использовали для поиска элементов в векторе, не работает для матриц. Вместо этого необходимо использовать функцию which() . Если мы хотим найти в матрице m позицию числа (8) , то вызов функции будет выглядеть так:

В данном случае видно, что результат возвращен в виде матрицы (1 times 2) . Обратите внимание на то, что колонки матрицы имеют названия. Попробуем использовать найденные индексы, чтобы извлечь искомый элемент:

Ура! Найденный элемент действительно равен (8) .

Еще один полезный способ создания матрицы — это собрать ее из нескольких векторов, объединив их по строкам. Для этого можно использовать функции cbind() и rbind() . На предыдущем занятии мы создали векторы с длиной и количеством станций на разных ветках метро. Можно объединить их в одну матрицу:

Cтроки и столбцы матрицы можно использовать как векторы при выполнении арифметических операций:

Результат можно присоединить к уже созданной матрице:

Содержимое матрицы можно просмотреть в более привычном табличном виде для этого откройте вкладку Environment и щелкните на строку с матрицей в разделе Data

Матрицы, однако, не дотягивают по функциональности до представления таблиц, и не предназначены для объединения разнородных данных в один набор (как мы это сделали). Если вы присоедините к матрице столбец с названиями веток метро, система не выдаст сообщение об ошибке, но преобразует матрицу в текстовую, так как текстовый тип данных способен представить любой другой тип данных:

При попытке выполнить арифметическое выражение над прежде числовыми полями, вы получите сообщение об ошибке:

2.1.3 Массивы

Массивы (arrays) — это многомерные структуры данных, с колчеством измерений 3 и более. Трехмерный массив представляет собой куб однородных данных. Для создания массива используется функция array() :

Массивы возникают тогда, например, когда имеются многомерные данные, зафиксированные по регулярной сетке географичесих локаций (это типично для геофизических данных). При этом 2 измерения отвечают за местоположение, а третье измерение — за временной срез или показатель.

Видео:Модуль вектора. Длина вектора.Скачать

2.2 Разнородные структуры данных

2.2.1 Фреймы данных

Фреймы данных — это обобщение понятия матрицы на данные смешанных типов. Фреймы данных — наиболее распространенный формат представления табличных данных. Для краткости мы иногда будем называть их просто фреймами.

Мы специально не используем для перевода слова data.frame термин ‘таблица’, поскольку таблица — это достаточно общая категория, которая описывает концептуальный способ упорядочивания данных. В том же языке R для представления таблиц могут быть использованы как минимум две структуры данных: фрейм данных (data.frame) и тиббл (tibble), доступный в соответствующем пакете. Мы не будем использовать тибблы в настоящем курсе, но после его освоения вы вполне сможете ознакомиться с ними самостоятельною

Для создания фреймов данных используется функция data.frame() :

К фреймам также можно пристыковывать новые столбцы:

Когда фрейм данных формируется посредством функции data.frame() и cbind() , названия столбцов берутся из названий векторов. Обратите внимание на то, что листинге выше столбцы имеют заголовки, а строки — номера.

Как и прежде, к столбцам и строкам можно обращаться по индексам:

Вы можете обращаться к отдельным столбцам фрейма данных по их названию, используя оператор $ (доллар):

Так же как и ранее, можно выполнять различные операции над столбцами:

Названия столбцов можно получить с помощью функции colnames()

Чтобы присоединить строку, сначала можно создать фрейм данных из одной строки:

Далее нужно убедиться, что столбцы в этом мини-фрейме называются также как и в том фрейме, куда мы хотим присоединить строку. Для этого нужно перезаписать результат, возвращаемый функцией colnames() :

Обратите внимание на синтаксис вышеприведенного выражения. Когда функция возвращает результат, она обнаруживает свойство самого объекта, и мы можем его перезаписать. После того как столбцы приведены в соответствие, можно присоединить новую строку:

Чтобы отсортировать фрейм данных по значению определенного поля, необходимо узнать порядок элементов в этом поле с помощью функции order() и проиндексировать им первое измерение фрейма:

Чтобы отфильтровать фрейм данных по значению определенного поля, необходимо передать условие в первое измерение фрейма:

Поскольку названия столбцов хранятся как вектор из строк, мы можем их переделать:

Обратимся по новому названию столбца:

К фреймам данных, так же как и к однородным структурам, можно применять функцию summary() для получения описательных статистик. При этом отчет формируется по каждому столбцу:

2.2.2 Списки

Список — это наиболее общий тип контейнера в R. Список отличается от вектора тем, что он может содержать набор объектов произвольного типа. В качестве элементов списка могут быть числа, строки, вектора, матрицы, фреймы данных — и все это в одном контейнере. Списки используются чтобы комбинировать разрозненную информацию. Результатом выполнения многих функций является список.

Например, можно создать список из текстового описания фрейма данных, самого фрейма данных и обобщающей статистики по нему:

Сооружаем список из трех элементов:

Можно дать элементам списка осмысленные названия при создании:

Теперь можно обратиться к элементу списка по его названию:

Поскольку summary сама является фреймом данных, из нее можно извлечь столбец:

К элементу списка можно также обратиться по его порядковому номеру или названию, заключив их в двойные квадратные скобки:

Использование двойных скобок отличает списки от векторов.

Вызов функции summary() в приложении к списку выведет статистику по типам и количеству элементов списка:

Видео:Нахождение длины вектора. Практическая часть. 9 класс.Скачать

2.3 Факторы

Понятие фактора в терминологии R используется для обозначения категориальной (качественной) переменной. Как известно, такие переменные могут быть номинальными (с неопределенным порядком) и порядковыми (с заданным отношением порядка). Проблема взаимодействия с категориальными переменными заключается в том, что они могут приобретать разнообразные формы: быть выражены в виде чисел и строк. Эта форма может быть обманчивой. Например, модели самолетов Boeing и Sukhoi SuperJet обознаются числами (747, 100 и т.д.). Однако очевидно, что складывать и вычитать такие числа смысла нет, они являются формой представления номинальной переменной. Другой пример: названия месяцев записываются в виде строк. Если попытаться отсортировать месяцы цветения различных видов деревьев, то получится бессмысленный алфавитный порядок, в котором апрель следует за августом. В данном случае проблема заключается в том, что мы имеем дело с категориальной переменной, в которой задан порядок следования допустимых значений.

В географических данных категориальные переменные тоже достаточно распространены. К номинальной шкале измерений относятся всевозможные числовые коды: почтовые, ОКАТО и т.д. К порядковой шкале — административный статус населенного пункта, сила землетрясения по шкале Рихтера. Для того, чтобы соответствующие данные в среде R правильно обрабатывались статистическими функциями и отображались в виде подходящих графических способов, необходимо явным образом проинформировать об этом программу. Для этого и создаются факторы.

Фактор построен по принципу ассоциативного массива и является надстройкой над вектором, в которой каждому значению вектора присваивается некий код. Вы можете управлять этими кодами, а можете оставить их на усмотрение программы.

Например, каждая линия Московского метро имеет свой номер. Создадим небольшей фрейм данных с электродепо по интересующим нас веткам метро и рассчитаем по ним описательные статистики:

Как видно, R посчитал нам средний номер линии метро — 3.091, что выглядит, мягко говоря, странновато. Чтобы этого не происходило, укажем в явном виде с помощью функции factor() , что номер линии метров является номинальной переменной:

Мы видим, что у переменной появился дополнительный атрибут Levels , который отвечает за список уникальных значений номинальной переменной. Отношение порядка мы здесь не вводим, поскольку номер является условным обозначением.

Попробуем теперь посчитать описательные статистики по переменной и таблице в целом:

Теперь мы видим, что вместо стандартных статистик R для переменной line_number выдает таблицу частот, из которой ясно, что на первой линии два депо, на второй линии три депо и так далее.

Видео:Типы векторов. Векторы (часть 3). Основы программирования на RСкачать

2.4 Описание структуры данных

Для описания структуры данных можно использовать две широко используемые диагностические функции: class() выведет тип структуры, а str() выведет детальную выписку по компонентам этой структуры:

Видео:Использование списков при создании функций в RСкачать

2.5 Циклы

Цикл — это разновидность управляющей конструкции, предназначенная для организации многократного исполнения набора инструкций. В R циклы наиболее часто используются для пакетной обработки данных, ввода и вывода. Типичными примерами использования циклов являются чтение множества файлов входных данных, а также построение серий графиков и карт одного типа по различным данным. При этом обработка множества строк таблиц в R обычно организуется не средствами циклов, а средствами функций семейства lapply , о которых мы поговорим в главе, посвященной техникам программирования на R.

Циклы обычно связаны с проходом по элементам списка/вектора либо с созданием такого списка/вектора. Поэтому они излагаются в настоящей главе.

В R, как и во многих других языках программирования, существует несколько вариантов циклов. Первый вид циклов — это конструкция for с синтаксисом for (x in X) statement . Она означает, что:

• переменная x должна пробежать по всем элементам последовательности X . В качестве последовательности может выступать любой вектор или список.
• каждый раз, когда x будет присвоено значение очередного элемента из X , будет выполнено выражение statement , которое называют телом цикла. Соответственно, цикл выполнится столько раз, сколько элементов содержится в последовательности X .

Выполнение тела цикла на каждом проходе называют итерацией.

Например, с помощью цикла можно вывести на экран числа от 1 до 10, по одному с каждой строки:

Если тело цикла содержит более одной инструкции R, оно должно быть заключено в фигурные скобки, иначе выполнится только первое выражение, а оставшиеся будут запущены один раз после выхода из цикла:

Другой вариант цикла организуется с помощью конструкции while , имеющей синтаксис while (condition) statement . Такая конструкция означает, что тело цикла будет выполняться, пока значение выражения condition (условия) равно TRUE . Как правило, в теле цикла обновляется некоторая переменная, которая участвует в проверке условия, и предполагается, что рано или поздно оно станет равным FALSE , что приведет к выходу из цикла. Например, вышеприведенный цикл, печатающий числа от 1 до 10, можно переписать на while следуюшим образом:

Обратите внимание на то, что мы внутри цикла обновляем значение переменной i.

Увеличение значения переменной цикла называется инкрементом, а уменьшение — декрементом.

Одной из самых распространенных ошибок программистов (особенно начинающих, но и професионалы ее не избегают) является забытая инструкция инкремента (или декремента) переменной цикла, в результате чего цикл становится бесконечным. В этом плане конструкция for более надежна.

В качестве примера приведем проход по столбцам фрейма данных и вычисление медианного значения для каждого столбца таблицы линий метро:

Существуют специальные операторы, позволяющие принудительно прервать текущую итерацию цикла и перейти на следующую, а также выйти из цикла вообще. Они называются next и break . Они бывают полезны, когда в теле цикла может произойти событие, делающее невозможным (или бессмысленным) его дальнейшее выполнение. Например, мы можем выводить информацию об электродепо, имеющихся на линии метро с введенным пользователем номером, до тех пор, пока он не введет символ q . Чтобы цикл был бесконечным, используем специальную форму while (TRUE) :

Оператор next используется реже, так как в принципе он взаимозаменяем с конструкцией if-else . Он бывет удобен, когда в длинном цикле имеется несколько мест, в которых возможен переход на следующую итерацию. При использовании next последующий код нет необходимости табулировать и забирать в скобки. Следующие паттерны идентичны, но вариант с next позволяет остаться на том же уровне вложенности:

Видео:Введение в R. Урок 12. Датафреймы в RСкачать

2.6 Технические детали

Внутреннюю структуру и размер объекта можно исследовать с помощью пакета lobstr. Например, посмотрим, как организован в пямяти объект metrolist :

Видео:2 37 Нахождение орта вектораСкачать

2.7 Краткий обзор

Для просмотра презентации щелкните на ней один раз левой кнопкой мыши и листайте, используя кнопки на клавиатуре:

Презентацию можно открыть в отдельном окне или вкладке браузере. Для этого щелкните по ней правой кнопкой мыши и выберите соответствующую команду.

Видео:МОДУЛЬ ВЕКТОРА длина вектора 10 и 11 классСкачать

2.8 Контрольные вопросы и упражнения

2.8.1 Вопросы

1. На какие две большие группы можно разделить структуры данных в R? Чем он отличаются?
2. Что такое вектор в языке R?
3. Какие способы создания векторов существуют?
4. Можно ли хранить в векторе данные разных типов?
5. Как определить длину вектора?
6. Как извлечь из вектора элемент по его индексу?
7. Как извлечь из вектора множество элементов по их индексам?
8. Как извлечь из вектора последний элемент?
9. С помощью какой функции можно сгенерировать последовательность чисел или дат с заданным шагом?
10. Как сгенерировать последовательность целых чисел с шагом 1, не прибегая к функциям?
11. Можно ли применять к векторам арифметические операторы и математические функции? Что будет результатом их выполнения?
12. С помощью какой функции можно отсортировать вектор? Как изменить порядок сортировки на противоположный?
13. С помощью какой функции можно найти индекс элемента вектора по его значению? Что вернет функция, если этот элемент встречается в векторе несколько раз?
14. Как работает функция ifelse() и для чего она используется?
15. Как работает функция summary() и для чего она используется?
16. Какая функция позволяет создать матрицу? По строкам или по столбцам заполняется матрица при использовании вектора как источника данных по умолчанию?
17. Как извлечь элемент по его индексам из матрицы, массива, фрейма данных, списка?
18. Как извлечь строку или столбец из матрицы или фрейма данных?
19. С помощью какого специального символа можно обратиться к столбцу фрейма данных по его названию?
20. Как получить или записать названия столбцов фрейма данных?
21. Как получить или записать названия строк фрейма данных?
22. Какая структура данных является результатом сортировки матрицы?
23. Какая функция позволяет осуществить транспонирование матрицы?
24. Какой оператор используется для умножения матриц? Каким критериям должны отвечать перемножаемые матрицы, чтобы эта операция была осуществима?
25. Как добавить новый столбец в фрейм данных? Опишите несколько вариантов.
26. Как добавить новую строку в фрейм данных?
27. Что произойдет, если к целочисленной матрице прибавить столбец, заполненный строками?
28. Какая функция позволяет находить индексы элементов матрицы или фрейма данных по их значениям?
29. Что такое цикл и для каких сценариев обработки данных могут быть полезны циклы?
30. Перечислите несколько способов организации циклов в R, необходимые ключевые слова и параметры.
31. Что такое инкремент и декремент?
32. Какое ключевое слово позволяет прервать цикл и выйти из него принудительно?
33. Какое ключевое слово позволяет прекратить текущую итерацию цикла и перейти сразу к новой итерации?
34. Являются ли необходимыми фигурные скобки в случае когда цикл или условный оператор содержит только одно выражение? Что говорит об этом стиль программирования на R?

2.8.2 Упражнения

Создайте вектор temp , в котором хранятся значения среднемесячных температур воздуха в городе Санкт-Петербурге (данные можно взять здесь). Напишите программный код, который вычисляет следующие вектора:

• количественное изменение температуры от месяца к месяцу (в градусах)
• качественное изменение температуры от месяца к месяцу ( ‘потепление’ или ‘похолодание’ );
• номера зимних месяцев (со среднемесячной температурой ниже нуля);
• описательные статистики среднемесячных температур (summary);

Выведите исходные и вычисленные данные в консоль (с пояснением что они означают).

Подсказка: для вычисления разностей между элементами вектора используйте функцию diff() .

На местности задан прямоугольник с координатами левого нижнего ( x1 , y1 ) и правого верхнего ( x2 , y2 ) угла. Напишите программу, которая размещает внутри этого прямоугольника случайным образом N точек и представляет результат в виде матрицы координат coords с двумя столбцами и N строками. Вызовите в конце программы plot(coords) , чтобы посмотреть на результат. Координаты можно не вводить, а задать прямо в программе в виде переменных.

Подсказка: координаты случайно размещенных точек имеют равномерное распределение. Вам необходимо сначала сформировать случайные векторы координат X и Y , и после этого объединить их в матрицу.

Высотная поясность на северном склоне Западного Кавказа, согласно Большой Российской энциклопедии устроена следующим образом:

• до 500 м — степь и лесостепь
• до 800 м — низкогорные широколиственные леса (дуб, граб)
• до 1300 м — среднегорные широколиственные леса (бук)
• до 1600 м — смешанные леса (ель, пихта, бук)
• до 2300 м — криволесия (береза, бук, клён)
• до 2500 м — субальпийские и альпийские луга
• до 3300 м — субнивальная зона (фрагментарная растительность)
• выше (условно до 5000 м) — гляциально-нивальная зона

Создайте фрейм данных, включающий три столбца: минимальная высота пояса ( Hmin ), максимальная высота пояса ( Hmax ) и название высотного пояса ( Zone ). Минимальную высоту надо вычислить на основе максимальной, приняв, что для нижнего пояса она условно равна (400

Напишите программу, которая просит пользователя ввести высоту и возвращает высотный пояс, соответствующую введенной высоте (достаточно вывести строчку фрейма данных).

Подсказка: Организуйте обход строчек фрейма данных с помощью цикла от (1) до (N) , где (N) — количество строк. Искомый пояс будет найден, как только введенное значение станет меньше чем Hmax . После этого можно вывести результат на экран. Если введенное значение больше максимума в столбце Hmax или меньше (400) , программа должна выдавать ошибку.

[advanced] Решите задачу №3, используя только операции над векторами и поиск элементов, и не используя циклы.

[advanced] Модифицируйте программу, написанную для решения задачи №2 таким образом, чтобы запретить точкам сближаться более чем на заданное расстояние k (это называется регулярным распределением с расстоянием ингибиции k). Сохраните результат в виде фрейма данных points со столбцами X, Y и D, где D – это расстояние до ближайшей точки. Выведите верхние строчки полученной таблицы в консоль, а также полученные точки с помощью команды plot(coords$X, coords$Y) .

Подсказка: вам придется генерировать в цикле по одной точке и проверять условие на каждой итерации до тех пор, пока вы не наберете требуемое количество точек. Задавайте значение k малым по отношению к размерам прямоугольника, чтобы избежать излишне долгого выполнения программы.

Видео:Введение в R. Урок 6. Создание функций в RСкачать

Введение в R: линейная алгебра

R — очень мощный язык, разработанный специально для анализа и визуализации данных и машинного обучения, что делает его обязательным к изучению для любого начинающего специалиста по данным.

R особенно удобен для линейной алгебры. Встроенные типы данных, такие как векторы и матрицы, хорошо сочетаются со встроенными функциями, такими как алгоритмы решения собственных значений и определителей, а также с возможностями динамического индексирования.

В этой вводной в статье про R рассмотрим следующие реализации линейной алгебры:

Векторы

• присваивание векторов;
• векторные операции;
• генерирование последовательностей;
• логические векторы;
• пропущенные значения;
• индексирование векторов.

Массивы и матрицы

• массивы;
• индексация массивов;
• индексация матриц;
• внешнее произведение двух матриц;
• демонстрация всех возможных определителей одноразрядных матриц 2×2;
• обобщённое транспонирование массива;
• умножение матриц;
• линейные уравнения и инверсия;
• собственные значения и собственные векторы;
• сингулярное разложение и определители;
• выравнивание методом наименьших квадратов и QR-разложение;
• формирование блочных матриц.

Видео:Векторы для начинающих. Коллинеарные векторы. Как найти длину вектора? Нулевой векторСкачать

Векторы

Присваивание векторов

R оперирует структурами данных, самой простой из которых является числовой вектор — упорядоченный набор чисел. Чтобы создать вектор x с четырьмя элементами 1 , 2 , 3 и 4 , можно использовать объединяющую функцию c() .

Здесь используется оператор присваивания , указывающий на назначаемый объект. В большинстве случаев можно заменить на = .

Также можно использовать функцию assign() :

Оператор y присвоит вектор 1, 2, 3, 4, 0, 1, 2, 3, 4 переменной y .

Векторы можно свободно перемножать и дополнять константами:

Заметьте, что эта операция верна, даже когда x и y имеют разную длину. В данном случае R просто будет повторять x (иногда дробно), пока не достигнет длины y. Поскольку y равен 9 числам в длину, а x — 4, x повторится 2.25 раз пока не совпадёт с длиной y.

Можно использовать все арифметические операторы: + , — , * , / и ^ , а также log , exp , sin , cos , tan , sqrt и многие другие. max(x) и min(x) отображают наибольший и наименьший элементы вектора x , а length(x) — количество элементов x ; sum(x) выдаёт сумму всех элементов x , а prod(x) — их произведение.

mean(x) вычисляет выборочное среднее, var(x) возвращает выборочную дисперсию, sort(x) возвращает вектор того же размера, что и x, элементы в котором расположены в порядке возрастания.

Генерация последовательностей

В R существует множество методов для генерации последовательностей чисел. 1:30 аналогичен c(1, 2, …, 29, 30) . Двоеточие имеет более высокий приоритет в выражении, поэтому 2*1:15 вернёт c(2, 4, …, 28, 30) , а не c(2, 3, …, 14, 15) .

30:1 используется для генерации последовательности в обратном направлении.

Для генерации последовательностей можно использовать и функцию seq() . seq(2,10) возвращает такой же вектор, что и 2:10 . В seq() , можно также указать длину шага: seq(1,2,by=0.5) возвращает c(1, 1.5, 2) .

Аналогичная функция rep() копирует объект различными способами. Например, rep(x, times=5) вернёт пять копий x впритык.

Логические векторы

Логические значения в R — TRUE, FALSE и NA. Логические векторы задаются условиями. val 13 задаёт val в качестве вектора той же длины, что x , со значением TRUE , если условие выполняется, и FALSE , если нет.

Логические операторы в R: , , > , >= , == и != , означающие, соответственно, меньше чем, меньше чем или равно, больше чем, больше чем или равно, равно или не равно.

Пропущенные значения

Функция is.na(x) возвращает логический вектор того же размера, что и x , со значение TRUE , если соответствующий элемент для x равен NA .

x == NA отличается от is.na(x) , поскольку NA является не значением, а маркером для недоступной величины.

Второй тип “пропущенного значения” создаётся численными вычислениями, например 0/0 . В этом случае значения NaN (не числа) рассматриваются как значения NA , то есть is.na(x) вернёт TRUE и для NA , и для NaN значений. is.nan(x) используется только для определения значений NaN .

Индексирование векторов

Первый вид индексации — через логический вектор. y устанавливает y значениям x , не равным NA или NaN .

(x+1)[(!is.na(x)) & x>0] -> z устанавливает z значениям x+1 , больше 0 и не являющимся Na или NaN .

Второй метод осуществляется с вектором положительных целых значений. В этом случае значения должны быть в наборе . Для формирования результата соответствующие элементы вектора выбираются и объединяются в этом порядке. Важно помнить, что, в отличие от других языков, в R первый индекс равен 1, а не 0.

x[1:10] возвращает первые 10 элементов x , предполагая, что length(x) не менее 10. c(‘x’, ‘y’)[rep(c(1,2,2,1), times=4)] создаёт символьный вектор длиной 16, где ‘x’, ‘y’, ‘y’, ‘x’ повторяются четыре раза.

Вектор отрицательных целых чисел определяет значения, которые должны быть исключены. y устанавливает y всем значениям x , кроме первых пяти.

Наконец, вектор символьных строк может использоваться, когда у объекта есть атрибут name для идентификации его компонентов. Для можно задать имя каждому индексу вектора names(fruit) . Затем элементы можно вызывать по имени lunch .

Преимущество этого подхода в том, что иногда буквенно-цифровые имена запомнить легче, чем индексы.

Обратите внимание, что индексированное выражение может встречаться на принимающей стороне присвоения, где оно только для этих элементов вектора. Например, x[is.na(x)] заменяет все значения NA и NaN в векторе x на 0 .

Другой пример: y[y аналогичен y — код просто заменяет все значения меньше 0 на отрицательные значения.

Видео:Списки в R. Объект ListСкачать

Массивы и матрицы

Массивы

Массив — это проиндексированный набор записей данных, не обязательно численный.

Вектор размерности — это вектор неотрицательных чисел. Если длина равна k, тогда массив k-размерный. Размерности индексируются от единицы вверх до значения, указанного вектором размерности.

Вектор может использоваться R в качестве массива, как атрибут dim . Если z — вектор из 1500 элементов, присвоение dim(z) означает, что z теперь представлен как массив 100 на 5 на 3.

Индексирование массивов

На индивидуальные элементы массива можно ссылаться, указав имя массива и в квадратных скобках индексы, разделённые запятыми.

Первое значение вектора a — 3 на 4 на 6 — может быть вызвано как a[1, 1, 1] , а последнее как a[3, 4, 6] .

a[,,] отображает массив полностью, следовательно, a[1,1,] берёт первую строку первого 2-размерного сечения a .

Индексирование матриц

Следующий код генерирует массив 4 на 5: x .

Массивы определяются вектором значений и размерностью матрицы. Значения вычисляются сначала сверху вниз, затем слева направо.

array(1:4, dim = c(2,2)) вернёт

В матрицах индексов запрещены отрицательные индексы, а значения NA и ноль разрешены.

Внешнее произведение двух матриц

Важной операцией с векторами является внешнее произведение. Если a и b — это два численных массива, их внешним произведением является массив, вектор размерности которого получается объединением двух векторов размерности, а вектор данных достигается формированием всех возможных произведений элементов вектора данных a и элементов вектора b . Внешнее произведение вычисляется с помощью оператора %o% :

Фактически любую функцию можно применить к двум массивам, используя внешнюю () функцию. Предположим, мы определили функцию f . Функцию можно применить к двум векторам x и y с помощью z .

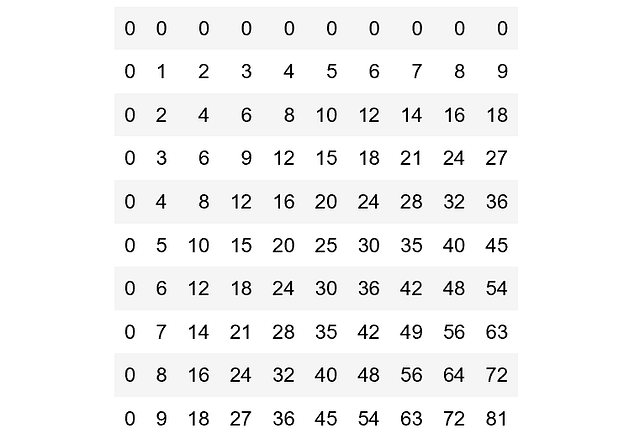
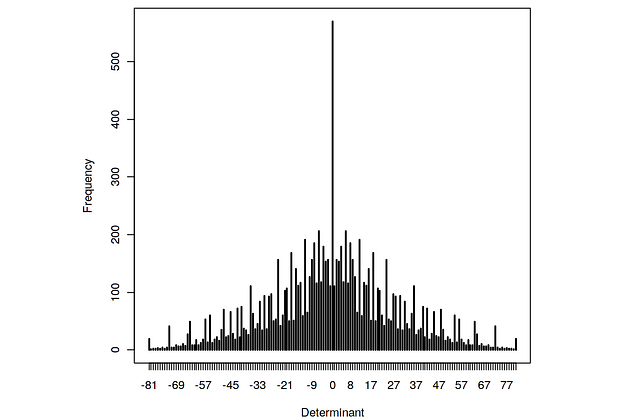
Демонстрация всех возможных определителей одноразрядных матриц 2×2

Рассмотрим определители матриц 2 на 2 [a, b; c, d], где каждая запись представляет собой неотрицательное число от 0 до 9. Задача: найти определители всех возможных матриц этой формы и отобразить на графике высокой плотности частоту, с которой встречается значение.

Или, перефразируя, нужно найти распределение вероятности определителя, если каждая цифра выбирается независимо и равномерно случайным образом.

Один из умных способов сделать это — использовать внешнюю функцию дважды.

Первая строка присваивает d этой матрице:

Вторая строка снова использует внешнюю функцию для расчёта всех возможных определителей. Последняя строка строит график.

Обобщённое транспонирование массива

Функция aperm(a, perm) используется для перестановки массива a. Аргументом perm должна быть перестановка чисел <1,…, k>, где k — количество индексов в a. Результатом функции будет массив того же размера, что и a, но прежняя размерность, заданная perm[j] , становится новой размерностью j-th .

Проще понять, если думать об этом как об обобщённом транспонировании матриц. Если A — это матрица, тогда B — просто результат перестановки матрицы A :

В таких особых случаях перестановку осуществляет функция t() .

Умножение матриц

Для умножения матриц используется оператор %*% . Если A и B являются квадратными матрицами одинакового размера, A*B — это поэлементное произведение двух матриц. A %*% B — это скалярное произведение (произведение матриц).

Если x — вектор, тогда x %*% A %*% x — его квадратичная форма.

crossprod() осуществляет перекрёстные произведения. Таким образом crossprod(X, y) аналогична операции t(X) %*% y , но более эффективна.

diag(v) , где v — вектор — задаёт диагональную матрицу с элементами вектора в качестве диагональных элементов. diag(M) , где m — матрица — задаёт вектор основных диагональных элементов M (так же как и в Matlab). diag(k) , где k — единичное числовое значение — возвращает единичную матрицу k на k .

Линейные уравнения и инверсия

Решение линейных уравнений является инверсией умножения матриц. Если

с заданными только A и b , вектор x — решение системы линейных уравнений, которое быстро решается в R:

Собственные значения и собственные векторы

Функция eigen(Sm) вычисляет собственные значения и собственные векторы симметричной матрицы Sm. Результат — это список, где первый элемент отображает значения, а второй — векторы. ev присваивает этот список ev .

ev$val — это вектор собственных значений Sm , и ev$vec — матрица соответствующих собственных векторов.

Для больших матриц лучше избегать вычисления собственных векторов, если они не нужны, используя выражение:

Сингулярное разложение и определители

Функция svd(m) принимает произвольный матричный аргумент m и вычисляет его сингулярное разложение. Оно состоит из 1) матрицы ортонормированных столбцов U с тем же пространством столбцов, что и m , 2) второй матрицы ортонормированных столбцов V , пространство столбцов которой является пространством строк m , 3) и диагональной матрицы положительных элементов D :

det(m) используется для вычисления определителя квадратной матрицы m .

Выравнивание методом наименьших квадратов и QR-разложение

Функция lsfit() возвращает список заданных результатов процедуры выравнивания методом наименьших квадратов. Присваивание наподобие этого:

выдаёт результаты выравнивания методом наименьших квадратов, где y — это вектор наблюдений, а X — проектная матрица.

ls.diag() используется для диагностики регрессии.

Тесно связанной функцией является qr().

Они вычисляют ортогональную проекцию y на диапазон X в fit , проекцию на ортогональное дополнение в res и вектор коэффициентов для проекции в b .

Формирование блочных матриц

Матрицы можно строить из других векторов и матриц с помощью функций cbind() и rbind() .

cbind() формирует матрицы, связывая матрицы горизонтально (поколоночно), а rbind() связывает матрицы вертикально (построчно).

В присвоении X аргументами cbind() должны быть либо векторы любой длины, либо столбцы одинакового размера (одинаковым количеством строк).

rbind() выполняет соответствующую операцию для строк.

🔍 Видео

Введение в R. Урок 15. Циклы в RСкачать

Длина вектора через координаты. 9 класс.Скачать

R Studio как пользоватьсяСкачать

Правила переписывания. Основы программирования на RСкачать

Как написать функцию в R?Скачать