Вписанные и описанные окружности история (4 видео)

Вписанная и описанная окружности

Содержание

«Управление общеобразовательной организацией: новые тенденции и современные технологии»
ИЗ ИСТОРИИ
О вписанных углах. Гиппократ Хиосский
Описанная и вписанная окружность
теория по математике 📈 планиметрия
Описанная окружность
Вписанная окружность
Вписанный и описанный треугольники
Вписанный и описанный четырехугольники
🎦 Видео

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

8 класс геометрия

Тема: Вписанная и описанная окружности.

Цели: ввести понятие вписанной и описанной окружностей; ввести понятие описанного около окружности и вписанного в окружность многоугольника; рассмотреть теоремы: об окружности, вписанной в треугольник; об окружности, описанной около треугольника; доказать свойства: описанного четырехугольника и вписанного четырехугольника.

Тип урока: изучение новой темы

Девиз урока: « Решай, ищи, твори и мысли».

I. Организационный момент.

II .Проверка домашнего задания. Актуализация опорных знаний.

Сформулируйте теорему о биссектрисе угла.

Что можете сказать о биссектрисах треугольника.

Что такое серединный перпендикуляр?

Сформулируйте теорему о серединном перпендикуляре к отрезку.

Что можете сказать о серединных перпендикулярах к сторонам треугольника.

Сформулируйте теорему о высотах треугольника.

Что это за замечательные точки треугольника?

IV . Изучение нового материала: презентация.

Ввести понятие вписанной в многоугольник окружности.

Ввести понятие описанного около окружности многоугольника.

Ввести понятие описанной около многоугольника окружности.

Ввести понятие вписанного в окружность многоугольника.

Ах, как долго мы писали,

Посмотрите все в окно, (Посмотреть влево — вправо.)

Мы глаза сейчас закроем, (Закрыть глаза ладошками.)

Вправо, влево повернем, а потом скатимся вниз, (Посмотреть вниз.)

VI . Закрепление изученного материала.

Вписанная и описанная окружности.

Построить три произвольных треугольника.

Провести биссектрисы углов.

Вписать окружность (центр окружности?).

Построить три произвольных треугольника.

Провести серединные перпендикуляры.

Описать окружности (центр окружности?).

— В любой треугольник можно вписать окружность, центр вписанной окружности – точка пересечения биссектрис.

-Около любого треугольника можно описать окружность, центр описанной окружности – точка пересечения серединных перпендикуляров.

Свойства четырехугольника, описанного около окружности.

— Построить три окружности, описать вокруг каждой четырехугольник АВСД.

-Измерить стороны каждого четырехугольника АВСД.

-Записать данные в таблицу.

-Найти сумму сторон АВ + СД и ВС + АД.

— В любом описанном около окружности четырехугольнике суммы противоположных сторон равно.

-Верно и обратное: Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.

Свойства четырехугольника, вписанного в окружность.

— Построить три окружности, вписать в каждую четырехугольник АВСД.

-Измерить углы каждого четырехугольника АВСД.

-Записать данные в таблицу.

-Найти сумму углов А + С и В + Д.

— В любом вписанном четырехугольнике сумма противоположных углов равна 180 градусов.

-Верно и обратное: Если сумма противоположных углов четырехугольника равна 180 градусов, то около него можно описать окружность.

V II . Итог урока. Домашнее задание выучить п. 77-78 решить №689 № 691 №693

Сказки об окружности

Жили в городе Геометрии Треугольник и Окружность. Треугольник был логичен, разумен, надёжен, в силу своей конструкции, но очень добр. Он спешил на помощь всем, кто в ней нуждался. Окружность была эмоциональна. Она любила весь мир и хотела, как можно больше вместить в себя, хотя где-то в глубине души, она считала себя ничтожно малой точкой, не имеющей никакой ценности во Вселенной.

Наша история началась тогда, когда волею судьбы Окружность оказалась вписанной в треугольник. Они познакомились и подружились. И было у них три точки касания, три точки соприкосновения: точка Деловых отношений, точка Дружеских отношений и точка Любви. Да, да, точка Любви, потому что Окружность всем сердцем полюбила Треугольник. Она сопротивлялась, мучилась, радовалась полёту своей души, страдала её падению, смущалась, но. не скрывала своего чувства. Умный Треугольник понимал её и принимал такой, какой она была. Он относился к ней трепетно и нежно и ещё надёжнее защищал своими тремя сторонами, защищал от злых языков, пустых разговоров и сплетен.

Шло время, и Окружности было бесконечно хорошо с Треугольником, ей хотелось быть с ним всё дольше и дольше, ей хотелось иметь с ним больше точек соприкосновения.

И вот однажды, Треугольник сказал ей: «Милая подружка, я знаю твои желания и могу их исполнить, но подумай. У нас с тобой есть обязательство перед теми, с кем мы встретились раньше. У тебя — перед твоим Диаметром, Хордой и Радиусом. У меня — перед моими тремя углами и медианой. Поверь, я очень хорошо отношусь к тебе, но, если я возьму на себя обязательства в отношениях с тобой, то просто не выдержу и сломаюсь».

У нашей Окружности было образное мышление и богатое воображение. Тотчас же перед её глазами появилась картинка: стороны треугольника сломались пополам и он исчез, превратившись в шестиугольник, но точек соприкосновения с ней стало в два раза больше. А дальше картинки менялись и мелькали как в калейдоскопе: в геометрической прогрессии стороны множились — шесть, двенадцать, двадцать четыре, сорок восемь, девяносто шесть. и вот уже исчез многоугольник, превратившись в окружность. Окружности стало страшно. «Мой Мудрый Друг», — сказала она, «я слишком люблю тебя и не хочу доставлять огорчения, не хочу, чтобы ты гнулся под грузом проблем. Я слишком люблю тебя и хочу спокойствия твоей душе. Пусть всё останется так, как прежде. Ведь у нас есть три точки соприкосновения: точка Деловых отношений, точка Дружеских отношений и точка Любви. Любовь ведь осталась! Я не буду напоминать тебе о ней, ты и так её чувствуешь, ты и так всё знаешь» Нам неизвестно, что творилось в душе Треугольника, только мы знаем, что он ответил: «Будем жить». «Будем жить!» — радостно повторила Окружность, хотя в её глазах стояли слезы.

История одной аппроксимации

Жила-была Окружность. Красавица была она — гладкая, ровненькая — ни излома, ни задоринки. Покладистая и спокойная, она была дружна со многими фигурами на плоскости, но особенно нравилась Окружность своему большому другу — описанному вокруг нее Треугольнику. Да и сама она была неравнодушна к нему. Правильный, точный, жесткий, строго хранящий свою форму, красавец Треугольник касался серединами сторон трех точек Окружности. Никакие внешние удары не могли изменить форму Треугольника, поэтому в его объятиях чувствовала себя Окружность защищенной от всех бед и тревог. Треугольнику тоже было приятно беречь и охранять свою любимую. Хорошо им было вместе. Не знаю, сколько бы это продолжалось, но однажды.
— Ах, милый, — прошептала Окружность, — Я очень счастлива, что мы с тобой вместе. Но что такое три точки? Придумай что-нибудь, постарайся для меня. Я так хочу, чтоб ты был еще ближе ко мне. Долго думал и мучился Треугольник, но разве можно было не уступить такой нежной просьбе. И вот, чтобы угодить любимой, изломал он каждую свою сторону, обрезал углы и стал Шестиугольником. Окружность была довольна, но. Прошло время, и шести точек ей показалось мало.

т Дальше — больше, стал Шестиугольник Двенадцати-, потом Двадцатичетырехугольником. Все тупее становились углы, все короче стороны. Шло время, и однажды Окружность удивилась: — Куда подевался мой друг? Тот самый Треугольник — строгий, жесткий, точный, надежно защищающий меня со всех сторон. Неужели вот это, нечто бесформенное, — ты, мой дорогой? А было уже девяносто шесть углов, и углы-то какие -176*15′. Действительно, Треугольника не стало, а то, что было, было почти окружностью, с большой точностью слившейся со своей подругой.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

ИЗ ИСТОРИИ

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

О вписанных углах. Гиппократ Хиосский

Изложенное в современных учебниках доказательство того, что вписанный угол измеряется половиной дуги, на которую он опирается, дано в «Началах» Евклида. На это предложение ссылается, однако, еще Гиппократ Хиосский (V в. до н. э.) в своем труде о «луночках». Труды Гиппократа свидетельствуют о том, что уже во второй половине V в. до н. э. было известно большое число теорем, изложенных в «Началах» Евклида, и геометрия достигла высокого развития.

Тот факт, что опирающийся на диаметр вписанный угол—прямой, был известен вавилонянам еще 4000 лет назад. Первое его доказательство приписывается Памфилией, римской писательницей времен Нерона, Фалесу Милетскому. Некоторые комментаторы Евклида полагают, что доказательство Фалеса, основанное на предложении, что сумма углов трёугольника равна 2d, было следующее: обозначив углы при диаметре через 1, 2, а части угла АВС, на которые он рассекается радиусом ОС, через 3, 4, получаем, с одной стороны:

с другой стороны: 1 + 2 + 3 + 4 = 2d,

откуда 2(З + 4) = 2d, З + 4 = d, т. е. АСВ = d.

Видео:ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Описанная и вписанная окружность

теория по математике 📈 планиметрия

Видео:ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Описанная окружность

Окружность называется описанной вокруг многоугольника, если все вершины многоугольника принадлежат этой окружности. Многоугольник в этом случае называется вписанным в окружность.

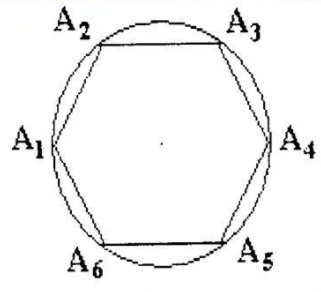
Любой правильный многоугольник можно вписать в окружность. На рисунке описанная окружность проходит через каждую вершину правильного шестиугольника.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Вписанная окружность

Окружность называется вписанной в многоугольник, если она касается всех его сторон. Многоугольник в этом случае называется описанным около окружности.

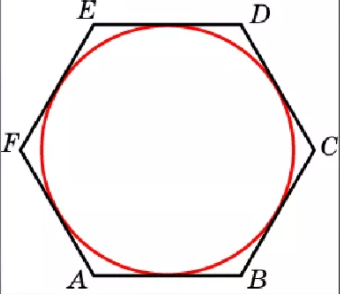
В любой правильный многоугольник можно вписать окружность. На рисунке окружность вписана в правильный шестиугольник, она касается всех его сторон.

Вписанный и описанный треугольники

Центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.

В любой треугольник можно вписать окружность: 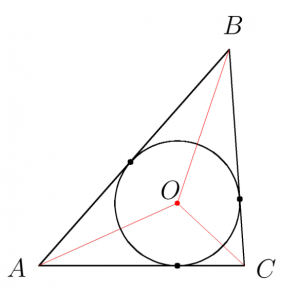Центр вписанной окружности

Центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.

Вписанный и описанный четырехугольники

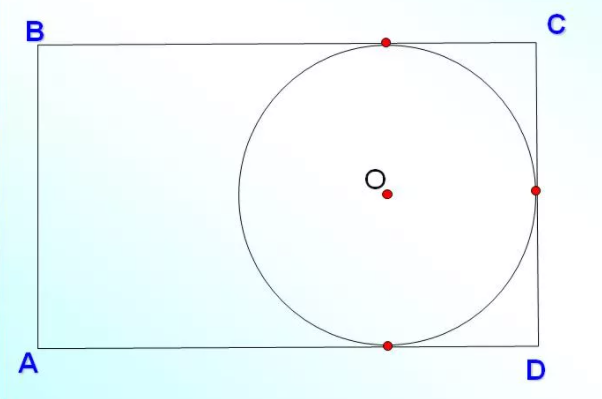
Не во всякий четырехугольник можно вписать окружность. Например, в прямоугольник нельзя вписать окружность. По рисунку видно, что окружность касается только трех его сторон, что не соответствует определению.

Условие вписанной в 4-х угольник окружности

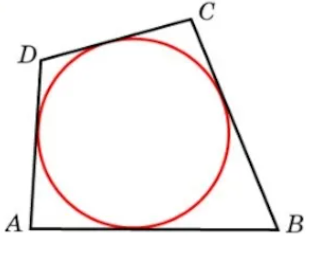
Окружность является вписанной в четырехугольник, если суммы длин противоположных сторон равны.

На рисунке выполняется данное условие, то есть AD + BC=DC + AB

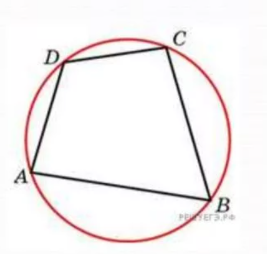
Окружность является описанной около четырехугольника, если суммы противоположных углов равны 180 градусов.

На рисунке окружности описана около четырехугольника, следовательно выполнено условие, что сумма углов А и С равна сумме углов B и D и равна 180 градусов.