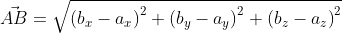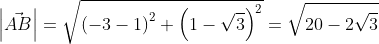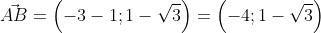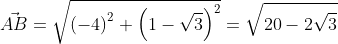1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;
8) основания, площади и уравнения биссекторов;
9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
| A ( ; ; ), B ( ; ; ), C ( ; ; ), D ( ; ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. Содержание
Видео:Высшая математика. 4 урок. Аналитическая геометрия. Вычисление объема тетраэдра.Скачать  Онлайн калькулятор. Модуль вектора. Длина вектораЭтот онлайн калькулятор позволит вам очень просто найти длину вектора для плоских и пространственных задач. Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление модуля вектора и закрепить пройденный материал. Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать  Калькулятор для вычисления длины вектора (модуля вектора) по двум точкам
Форма представления вектора: Инструкция использования калькулятора для вычисления длины вектораВвод даных в калькулятор для вычисления длины вектора (модуля вектора)В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.. Дополнительные возможности калькулятора для вычисления длины вектора (модуля вектора)
Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать  Вычисления длины вектора (модуля вектора)Например, для вектора a = <ax; ay; az> длина вектора вычисляется cледующим образом: Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел. Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! Добро пожаловать на OnlineMSchool. Видео:Нахождение длины вектора. Практическая часть. 9 класс.Скачать  Длина вектора — основные формулыВремя чтения: 16 минут Видео:Равенство векторов, Длина вектора.Как найти длину вектора?Скачать  Основные понятия вектораДля того чтобы приступить к разбору формул нахождения длины вектора, необходимо разобраться в основных понятиях и определениях векторов. Понятие вектора получило широкое распространение в 19 веке, в математических науках, особенно в таком её разделе, как «Комплексные числа». Вектор — это отрезок с определённой длиной и направлением. Графическое изображение вектора — отрезок который имеет указание направления в виде стрелки. Вектор, который будет иметь начальную точку Х и конец в точке А, правильно обозначать ХА, с верхним подчёркиванием или стрелочкой, а также допустимо прописывать одной прописной буквой. Длину вектора (модуль), определяет числовое значение длины отрезка, имеющего направление. Обозначается длинна двумя вертикальными отрезками |ХА|.
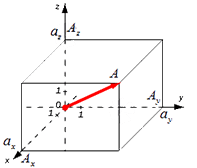
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные. Вектора могут находится не только на плоскости, но и в пространстве, от этого расположения будет зависеть какую формулу необходимо использовать для нахождения их длины или модуля. Стоит также отметить, что вектора могут быть равными, при этом они должны иметь одно направление, одинаковые длины и быть коллинеарными. Существует понятие единичного вектора, таким он будет являться если равен единице измерения. Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать  Как найти длину вектораМодуль вектора а будем обозначать Для того чтобы найти модуль вектора или его длину, на плоскости по координатам, необходимо рассмотреть вектор используя прямоугольную декартову систему координат Оxy. Допустим в данной системе будет задан, так вектор На взятой системе координат, от её начала отложим вектор Далее используя теорему Пифагора мы получим равенство АО² = ОAₓ² и OAᵧ², отсюда следует Теперь в соответствии с определением вектора относительно прямоугольной оси координат выходит, что ОAₓ² = aₓ² и также для OAᵧ² = aᵧ² , а так как на построенном прямоугольнике мы видим, что ОА равна длине вектора Из вышесказанного выходит, что для того чтобы найти длину вектора с точками (aₓ ; aᵧ), выводим следующую формулу: Когда вектор Чтобы рассчитать длину Чтобы найти модуль вектора используем ранее приведённую формулу Ответ: Существуют также формулы вычисления длины вектора в пространстве, они выводятся аналогично тем, что в системе координат на плоскости. Если взять вектор В таком случае ( AO^2=OA_x^2+OA_y^2+OA_z^2 ) (из рисунка видно, что АО — диагональ прямоугольного параллелепипеда), поэтому из определения получаются равенства ОAₓ=aₓ; OAᵧ=aᵧ; OA Ответ: Видео:Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать  Длина вектора через координаты точек начала и концаРанее мы рассмотрели формулы, которые позволят находить длину вектора используя при этом координаты. Рассматривались примеры в трёхмерном пространстве на плоскости. Используя данные формулы можно найти длину вектора, если известны координаты точек его начала и конца. Возьмём точки с обозначенными координатами начала A(aₓ ; aᵧ) и конца В(bₓ ; bᵧ), из чего следует, что вектор При этом формула вычисления длины вектора Для прямой системы координат, найти длину вектора ( overrightarrow) , где A(1,√3) B(-3,1) Решение Ответ: Найти, решения, при подстановке которых, длина вектора будет равна корню из тридцати, при координатах точек А (0,1,2) и В (5,2,(λ^2)) В первую очередь представим длину вектора в виде формулы. Видео:№320. В тетраэдре ABCD точки М, N и К— середины ребер АС. ВС и CD соответственноСкачать  Длина вектора по теореме косинусовТак как бывают случаи, когда не известны координаты точек вектора, необходимо искать другие варианты, при помощи которых можно найти длину вектора. Таким способов может стать применение теоремы косинусов. К примеру, нам известны длины двух векторов (overrightarrow) и (overrightarrow) , а также угол между ними, или его косинус. При этом необходимо найти длину вектора ( overrightarrow ) , в таком варианте задания необходимо воспользоваться теоремой косинусов, представив треугольник АВС. В данном треугольнике мы будем искать сторону ВС, она и будет равна длине искомого вектора. Подробнее рассмотрим на примере. Даны длины двух векторов ( overrightarrow) и ( overrightarrow) 2 и 4 соответственно, а угол между ними равен ( frac ) . необходимо найти длину ( overrightarrow). В нашем примере длины векторов и длины сторон треугольника АМК совпадают. Две из сторон нам известны это АК и АМ, а также известен угол треугольника, находящийся между этими сторонами. Используя теорему косинусов получим: Теперь мы видим, что для нахождения длины вектора существует несколько формул, которыми можно воспользоваться в зависимости от известных параметров. длина вектора формула для трёхмерного пространства; длина вектора формула по известным координатам начала и конца вектора находящегося пространстве; ( left|vecright|=sqrt) если известны координаты начала и конца вектора на плоскости. Существует также формула длины вектора перемещения: ( left|vec В случае если известен угол, между двумя векторами, можно использовать теорему Пифагора. Видео:Площадь параллелограмма, построенного на данных векторахСкачать  Применение векторов в других сферахПонятие и вычисление вектора важно не только в математике, но и других науках:
Векторы используются не только в науках, но и различных отраслях и профессиях. В судоходстве и аэрофлоте, архитектуре и конструировании, а также многих других областях. Для того чтобы найти длину вектора, мы можем использовать одну из формул, в зависимости от того, что нам о нём известно, и в каком пространстве или плоскости находится неизвестный вектор. 📽️ ВидеоВычисляем высоту через координаты вершин 1Скачать  10 класс, 12 урок, ТетраэдрСкачать  Угол между векторами | МатематикаСкачать  Найти длину вектора и середину отрезкаСкачать  Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать  Решение пирамидыСкачать  Длина вектора через координаты. 9 класс.Скачать  Найти длину вектора в прямоугольникеСкачать  №369. Медианы грани ABC тетраэдра ОABC пересекаются в точке М. Разложите вектор ОАСкачать  Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать  МОДУЛЬ ВЕКТОРА длина вектора 10 и 11 классСкачать  | |
 Размерность вектора:
Размерность вектора:
 .
. имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора
имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора 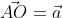 В соответствии с проекцией точки А возьмём и определим Aₓ и Aᵧ на оси координат. Рассмотрим полученный прямоугольник ОAₓ и АAᵧ с диагональю ОА.
В соответствии с проекцией точки А возьмём и определим Aₓ и Aᵧ на оси координат. Рассмотрим полученный прямоугольник ОAₓ и АAᵧ с диагональю ОА.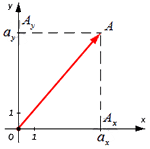
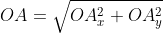
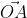 получаем
получаем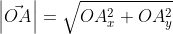

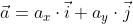 , то вычислить его можно по той же формуле
, то вычислить его можно по той же формуле 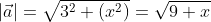
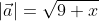
 )
)
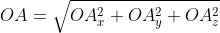
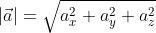
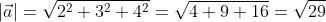
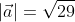
 имеет координаты (bₓ-aₓ ; bᵧ-aᵧ), поэтому его длину мы выразим в формуле
имеет координаты (bₓ-aₓ ; bᵧ-aᵧ), поэтому его длину мы выразим в формуле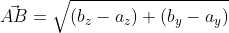
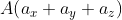 и
и 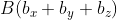 ), будет следующей:
), будет следующей: