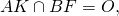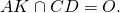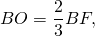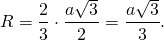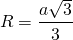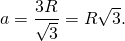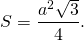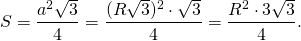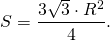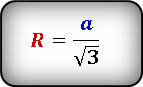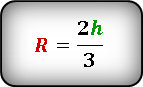Окружность, описанная около правильного треугольника, обладает всеми свойствами описанной около произвольного треугольника окружности и, кроме того, имеет свои собственные свойства.
1) Центр описанной около треугольника окружности — точка пересечения серединных перпендикуляров к его сторонам.
Поскольку в равностороннем треугольнике медианы, высоты и биссектрисы совпадают, центр описанной около правильного треугольника окружности лежит в точке пересечения его медиан, высот и биссектрис.
Например, в правильном треугольнике ABC AB=BC=AC=a
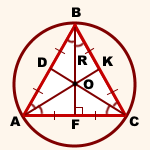
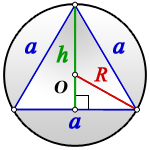
точка O — центр описанной окружности.
AK, BF и CD — медианы, высоты и биссектрисы треугольника ABC.
2) Расстояние от центра описанной окружности до вершин треугольника равно радиусу. Так как центр описанной около равностороннего треугольника окружности лежит на пересечении его медиан, а медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то радиус описанной окружности составляет две трети от длины медианы:
Таким образом, формула радиуса описанной около правильного треугольника окружности —
И обратно, сторона равностороннего треугольника через радиус описанной окружности —
3) Формула для нахождения площади правильного треугольника по его стороне —
Отсюда можем найти площадь через радиус описанной окружности:
Таким образом, формула площади площади правильного треугольника через радиус описанной окружности —
4) Центр описанной около правильного треугольника окружности совпадает с центром вписанной в него окружности.
5) Радиус описанной около равностороннего треугольника окружности в два раза больше радиуса вписанной окружности:
Видео:Как найти диаметр окружности, описанной около равнобедренного треугольникаСкачать
Радиус описанной окружности равностороннего треугольника
Свойства
Зная радиус описанной окружности, можно найти сразу не только сторону равностороннего треугольника, но и радиус вписанной в него окружности, так как они напрямую связаны друг с другом. Сторона треугольника будет равна произведению радиуса описанной окружности на корень из трех, а радиус вписанной окружности – его половине. (рис.100) a=√3 R r=R/2
Чтобы вычислить периметр и площадь равностороннего треугольника через радиус описанной вокруг него окружности, необходимо подставить полученное выражение для стороны в соответствующие формулы. P=3a=3√3 R S=(√3 a^2)/4=(3√3 R^2)/4
Высоты, медианы и биссектрисы являются одними и теми же отрезками в равностороннем треугольнике, и вычислить их можно по единой формуле, где искомая величина равна корню из трех, умноженному на сторону и деленному на два. Подставив вместо стороны произведение радиуса и корня из трех, получаем, что высота равна трем радиусам, деленным на два. (рис.99) h=m=l=(√3 a)/2=(√3 √3 R)/2=3R/2
Чтобы найти среднюю линию равностороннего треугольника через радиус описанной вокруг него окружности, необходимо разделить произведение радиуса и корня из трех на два. (рис.97.3) M=(√3 R)/2
Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать
Радиус описанной окружности равностороннего треугольника
— сторона треугольника
— высота
— радиус описанной окружности
Формула радиуса описанной окружности равностороннего треугольника через его сторону:
Калькулятор — вычислить, найти радиус описанной окружности равностороннего треугольника по стороне
Формула радиуса описанной окружности равностороннего треугольника через высоту:
Калькулятор — вычислить, найти радиус описанной окружности равностороннего треугольника по стороне
📺 Видео
ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать
найти радиус окружности, описанной вокруг треугольникаСкачать
Свойство окружности, описанной около равнобедренного треугольникаСкачать
Окружность вписана в равносторонний треугольник, найти радиусСкачать
Радиус окружности описанной около равностороннего треугольникаСкачать
Геометрия Найдите радиус окружности описанной около равнобедренного треугольника с основанием 16 смСкачать
ЕГЭ 6 номер. Нахождение диаметра описанной окружности около равнобедренного треугольникаСкачать
КАК НАЙТИ ДЛИНУ ОКРУЖНОСТИ, ОПИСАННОЙ ОКОЛО ПРАВИЛЬНОГО ТРЕУГОЛЬНИКА? Примеры | ГЕОМЕТРИЯ 9 классСкачать
Задание 16 ОГЭ по математике. Окружность описана около равностороннего треугольника. Задача 2Скачать
Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать
Нахождение диаметра описанной окружностиСкачать
Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать
Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать
Задача 6 №27923 ЕГЭ по математике. Урок 140Скачать
Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать
Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать
Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать
ОГЭ 2020 задание 17Скачать
