Как найти биссектрису треугольника транспортиром (6 видео)

Как построить биссектрису данного угла? Задачи на построение

Существует такой забавный детский стишок, с помощью которого легко запомнить, что такое биссектриса: «Биссектриса — это такая крыса, что бегает по углам и делит угол пополам». Однако нельзя забывать, что, несмотря на простоту запоминания этого шуточного определения, учитель справедливо потребует другое, взятое из учебника.

В дальнейшем изучении школьной программы дети сталкиваются со сложной с первого взгляда задачей — как построить биссектрису данного угла с помощью циркуля. Однако уже более продвинутый школьник без труда справится с этим заданием, которое является основой выполнения цикла задач на построение в геометрии. Давайте же разберемся с этим вопросом раз и навсегда.

Содержание

Как построить биссектрису данного угла?
Алгоритм построения
Доказательство
как построить биссектрису с помощью транспортира и линейки
Вычисление биссектрисы треугольника с известными свойствами
Свойства
Свойства в равнобедренных треугольниках
Определение биссектрисы треугольника
Определение длины
Нахождение величины угла
🎥 Видео

Видео:Построение биссектрисы в треугольникеСкачать

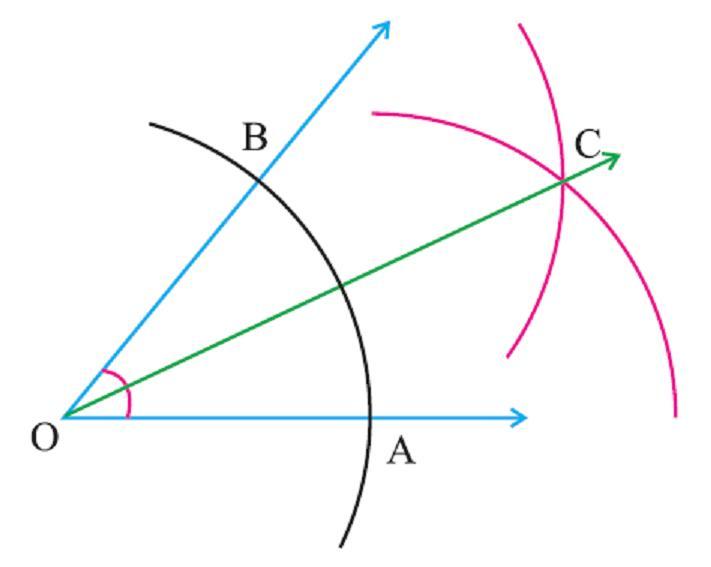
Как построить биссектрису данного угла?

Вам будет интересно: Французский язык: спряжение vivre

Самым очевидным и наиболее простым способом является использование транспортира, но если данного вспомогательного инструмента не оказалось под рукой, надо уметь строить биссектрису без него.

Для выполнения данной задачи, как уже понял читатель, нам потребуется циркуль, а помимо него — линейка (важно понимать, что делениями на ней пользоваться нельзя) и простой карандаш с ластиком.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Алгоритм построения

Необходимо совершить такие действия:

Установите иглу циркуля в вершине данного угла.

Установите циркулем произвольный радиус, проверните инструмент так, чтобы нарисованная им дуга пересекала оба луча, образующие угол.

Отметьте точки пересечения дуги со сторонами заданного угла.

Переставьте иглу циркуля в одну из отмеченных точек, выберете произвольный радиус и снова проверните циркуль таким образом, чтобы нарисованная им дуга была заключена внутри угла.

Аналогичные действия проделайте, передвинув циркуль в точку, отмеченную на другой стороне угла. Важно сохранить радиус, выбранный в предыдущем пункте алгоритма.

Отметьте точку пересечения двух дуг, которые были начерчены в двух предыдущих пунктах.

Проведите луч из вершины угла, проходящий через эту точку.

Полученный луч является искомым.

Мы дали ответ на поставленный вопрос — как построить биссектрису данного угла.

Видео:№102. Начертите треугольник. С помощью транспортира и линейки проведите его биссектрисы.Скачать

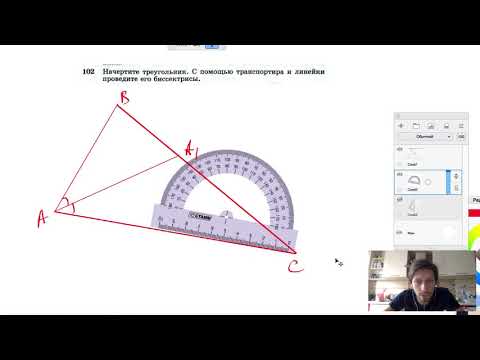
Доказательство

Теперь, разобравшись, как построить биссектрису данного угла, стоит вспомнить еще одно определение биссектрисы, используя термин «геометрическое место точек». Биссектрисой называется геометрическое место точек, которые равноудалены от лучей, образующих угол.

Согласно выполненному построению в пунктах 4-6, точка, принадлежащая построенной биссектрисе, также принадлежит двум окружностям, равным по радиусу, центр которых располагается на лучах, образующих угол на одинаковом расстоянии от вершины угла (согласно пунктам 1-3 построения). Опустим перпендикуляр из отмеченной в пункте 6 точки на лучи, образующие угол. Докажем, что получившиеся прямоугольные треугольники равны, и выясним, что опущенные перпендикуляры также равны, как соответствующие элементы треугольников. Таким образом, их общая гипотенуза является биссектрисой угла по определению. Что и требовалось доказать.

Видео:№43. Начертите угол, равный 70°, и с помощью транспортира проведите его биссектрису.Скачать

как построить биссектрису с помощью транспортира и линейки

Транспортиром измерить угол, для которого строим биссектрису. Полученное число разделить на 2. Поставить там точку, соединить её с вершиной угла по линейке.

измерь основной угол, значение подели на 2. поставь около получившегоя значения точку, убери транспортир, соедини эту точку с началом угла. встречный вопрос: как разделить 0,8 литра водки на троих?

начерти треугольник внутри соединни обин угол с серединой другой стороны

Видео:Построение биссектрисы углаСкачать

Вычисление биссектрисы треугольника с известными свойствами

Математика, как известно, царица наук. Неслучайно это выражение так любят учителя, особенно старой формации. Математика открывается исключительно тем, кто умеет, во-первых, логически мыслить, а во-вторых, тем, кто любит всегда добиваться ответа, оперируя изначальными условиями, не жульничая, а основывая решения на анализе, построение опять-таки логических связей. Эти качества, вынесенные со школьной скамьи, способны модулироваться и к взрослой серьезной жизни как в рабочих, так и в иных сложных моментах.

Свойства
Свойства в равнобедренных треугольниках
Определение биссектрисы треугольника
Определение длины
Нахождение величины угла

Сегодня многие сталкиваются с проблемами при решении математических задач еще в начальной школе.

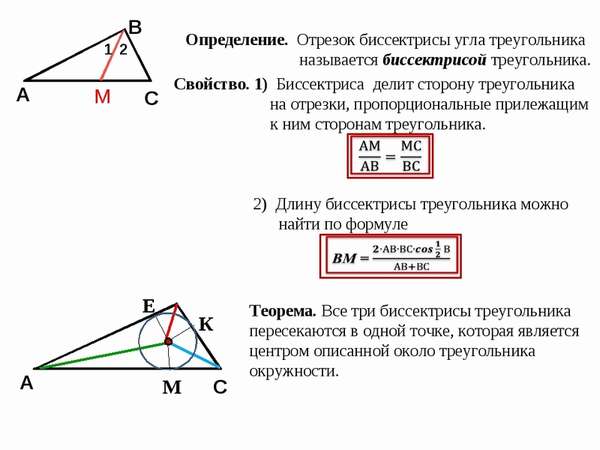
Однако даже те школьники, которые успешно осваивают первичную математическую программу, переходя на новый школьный и жизненный этап, где алгебра отделяется от геометрии, бывает, сталкиваются с серьезными затруднениями. Между тем, один раз выучив и, главное, поняв, как найти биссектрису треугольника, ученик навсегда запомнит эту формулу. Рассмотрим треугольник ABC с тремя проведенными биссектрисами. Как видно из рисунка, все они сходятся в одной точке.

Во-первых, определим, что биссектриса треугольника, и это одно из важнейших ее свойств, делит угол, из которого такой отрезок исходит, пополам. То есть в приведенном примере угол BAD равен углу DAC.

Это интересно: Как найти периметр треугольника.

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Свойства

Биссектриса треугольника разделяет сторону, к которой она проведена на два отрезка, обладающие свойствами пропорциональности к сторонам, которые прилегают к каждому отрезку, соответственно. Таким образом, BD/CD = AB/AC.
Каждый треугольник способен обладать тремя данными отрезками. Другие значимые свойства касаются как частных, так и общих случаев конкретных рассматриваемых треугольников.

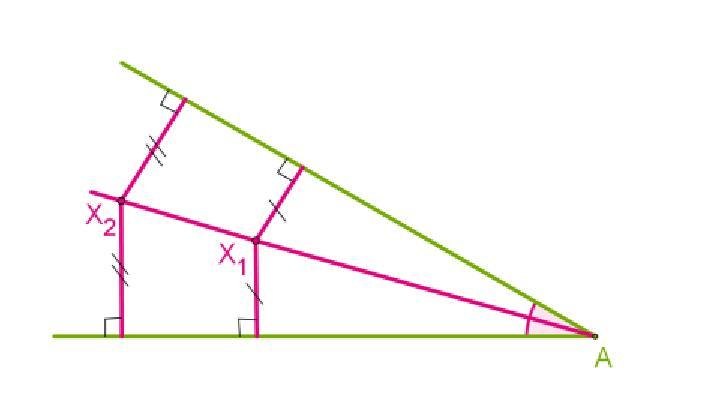
Свойства в равнобедренных треугольниках

Первое свойство биссектрис равнобедренного треугольника формулируется в том, что равенство двух биссектрис свидетельствует о равнобедренности этого треугольника. Третья же его биссектриса медиана, а также высота его угла.
Разумеется, что будет верным и обратное свойство. То есть в равнобедренном треугольнике неизменно наблюдается равенство двух его биссектрис.
Из сказанного ранее вытекает вывод о том, что биссектриса, исходящая из противоположного основанию, служит также медианой и высотой.
Все биссектрисы равностороннего треугольника обладают равенством.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Определение биссектрисы треугольника

Допустим, что в рассматриваемом треугольнике ABC сторона AB = 5 cm, AC = 4 cm. Отрезок CD = 3 cm.

Определение длины

Определить длину можно по следующей формуле. AD = квадратный корень из разности произведения сторон и произведения пропорциональный отрезков.

Найдем длину стороны BC.

Из свойств известно, что BD/CD = AB/AC.
Значит, BD/CD = 5/4 = 1,25.
BD/3 = 5/4.
Значит, BD = 3,75.
ABxAC = 54=20.
CDxBD = 33,75 = 11,25.

Так, для того чтобы рассчитать длину, требуется вычесть из 20 11,25 и извлечь квадратный корень из получившегося 8,75. Результат с учетом тысячных долей получится 2,958.

Данный пример призван также эксплицитно указать на ситуацию, когда значения длины биссектрисы, как и все другие значения в математике, будут выражены не в натуральных числах, однако бояться этого не стоит.

Это интересно: в чем выражается эволюционный характер развития общества?

Нахождение величины угла

Для нахождения углов, образующихся биссектрисой, важно, прежде всего, помнить о сумме углов, неизменно составляющей 180 градусов. Предположим, что угол ABC равен 70 градусам, а угол BCA 50 градусам. Значит, путем простейших вычислений получим, что CAB = 180 (70+50) = 60 градусов.

Если использовать главное свойство, в соответствии с которым угол, из которого она исходит, делится пополам, получим равные значения углов BAD и CAD, каждый из которых будет 60/2 = 30 градусов.

Если требуется дополнительный наглядный пример, рассмотрим ситуацию, когда известен лишь угол BAD равный 28 градусам, а также угол ABC равный 70 градусам. Используя свойство биссектрисы, сразу найдем угол CAB путем умножения значения угла BAD на два. CAB = 282 =56. Значит, BAC = 180 (70+56) или 180 (70+282)= 180 126 = 54 градуса.

Специально не рассматривалась ситуация, когда данный отрезок выступает в качестве медианы или высоты, оставив для этого другие специализированные статьи.

Таким образом, мы рассмотрели такое понятие, как биссектриса треугольника, формула для нахождения длины и углов которой заложена и реализована в приведенных примерах, имеющих целью наглядно показать, каким образом можно использовать для решения тех или иных задач в геометрии. Также к данной теме относятся такие понятия, как медиана и высота. Если данный вопрос прояснился, следует обращаться к дальнейшему изучению различных других свойств треугольника, без которых немыслимо дальнейшее изучение геометрии.

Биссектриса треугольника