Как начертить двадцатичетырехугольник в окружности с помощью циркуля (8 видео)

Построение правильных многоугольников

Содержание

Окружность. Круг. Приемы работы циркулем, использование трафаретов
Ход занятия:
Организационный момент:
Повторение:
Новый материал:
Физкультурная пауза.
Закрепление:
Запомни:В центре должны обязательно пересекаться штрихи, проведенных центровых (осевых) линий, а не точки.В окружностях меньших размеров допускается проводить вместо штрихпунктирных линий тонкие линии построения.
С помощью циркуля и линейки опишите около окружности правильный четырёхугольник.
📹 Видео

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Тема этого видеоурока – «Построение правильных многоугольников». На данном занятии мы рассмотрим способы построения правильных многоугольников с помощью циркуля и линейки. Также еще раз дадим определение правильному многоугольнику, изобразим его графически, после чего еще раз убедимся, что центры вписанной и описанной окружностей вокруг такой фигуры будут совпадать.

Видео:Построение пятиугольника циркулем и линейкойСкачать

Окружность. Круг. Приемы работы циркулем, использование трафаретов

Цели и задачи:

Дать определение окружность, круг.
Научить делить окружность на равные части.
Научить выполнять геометрические построения при помощи циркуля и трафаретов.
Ознакомить с применением данных геометрических построений в различных областях деятельности человека.
Воспитывать терпение, аккуратность при выполнении заданий.

Тип урока: комбинированный.

Формы работы: индивидуальная, групповая.

Видео:Как построить квадрат, два способаСкачать

Ход занятия:

Организационный момент:

Проверка готовности к уроку.

Повторение:

Анализ графического упражнения.

Новый материал:

Рубрика «Это интересно!»

С незапамятных времен человек использовал в своей жизни простейшие геометрические построения. Одним из таких построений является деление окружности на равные части. Примеров можно привести много. Превращение колеса из сплошного диска в обод со спицами поставило человека перед необходимостью распределить спицы в колесе равномерно.

С делением окружности неразрывно связано построение правильных многоугольников. Правильные многоугольники встречаются в древнейших орнаментах у всех народов.

В декоративно- прикладном искусстве дизайнеры, ювелиры и представители многих других профессий с успехом применяли деление окружности, создавая прекрасные произведения. Это ордена, медали, монеты и ювелирные украшения.

Орден Красной Звезды
Орден Отечественной войны

Самым распространенным примером применение деления окружности на равные части является создание логотипов, эмблем, товарных знаков различных фирм. Иногда достаточно увидеть эмблему на капоте или крыле автомобиля и безошибочно назвать марку.

Показ наглядных пособий использования геометрических построений в строительстве, архитектуре, машиностроении, а также природные явления.

Построение круга, окружности.

Круг – это часть плоскости, ограниченная окружностью.

Окружность – замкнутая плоская кривая, все точки которой равноудалены от центра.

Чтобы изобразить круг, достаточно взять блюдце или тарелку и обвести.

Для построения окружности необходимо найти центр. Из центра циркулем провести окружность.

Этапы построения:

Начертить квадрат.
Разделить стороны квадрата на две равные части, отметить буквами или цифрами.
Через полученные точки провести центровую линию (штрихпунктирную) Сначала горизонтальную, затем вертикальную.
Пересечение линий отметить точкой О – центр окружности.
В точку О поставить ножку циркуля и начертить окружность. Центр окружности является также и центром круга.

Запомнить: в центре должны обязательно пересекаться штрихи, проведенных центровых (осевых) линий, а не точки. В окружностях меньших размеров допускается проводить вместо штрихпунктирных линий тонкие линии построения.

Для построения окружностей и кругов используют трафареты.

Демонстрация, показ.

Деление окружности на равные части.

Любая прямая, проведенная через центр окружности, делит эту окружность на две равные части. Две взаимно перпендикулярные прямые, проведенные через центр окружности, делят эту окружность на 4 равные части.

Окружность можно разделить на 8 равных частей, используя линейку или угольники.

Демонстрация, показ.

Если соединить, полученные при делении точки окружности, то мы получим правильные многоугольники.

При делении окружности на 3, 6, 12 равных частей используют не только угольники, но и циркуль. В результате построения можно увидеть правильный равносторонний треугольник, правильный шестиугольник (рисунок 5)

Демонстрация, показ.

Физкультурная пауза.

Закрепление:

Фрагмент из рабочей тетради.

Приготовь для работы циркуль, карандаш с маркировкой Т и ТМ, линейку, трафарет. Все построения выполняй аккуратно.

Используя трафарет с окружностями, изобрази круг.

Для построения окружности необходимо провести штрихпунктирные линии. Эти линии состоят из штриха и точки. При пересечении они образуют центр окружности и являются центровыми или осевыми линиями.

Установи ножку циркуля в центре пересечения осевых (центровых) линий и проведи окружность.

Этапы построения окружности:

Начертить квадрат.
Разделить все стороны квадрата на две равные части, отметить полученные точки.
Через точки провести центровую линию (штрихпунктирную) карандашом с маркировкой Т. Сначала горизонтальную, затем вертикальную.
Пересечение линий отметить точкой О – центр окружности.
В точку О поставить ножку циркуля и начертить окружность.

Центр окружности является также и центром круга.

Запомни:
В центре должны обязательно пересекаться штрихи, проведенных центровых (осевых) линий, а не точки.
В окружностях меньших размеров допускается проводить вместо штрихпунктирных линий тонкие линии построения.

Рубрика «ЗАПОМНИ»: круг, окружность, осевая линия, центровая линия, штрихпкнктирная линия.

Видео:Построение пятиугольника циркулемСкачать

С помощью циркуля и линейки опишите около окружности правильный четырёхугольник.

То есть у нас есть окружность, а вокруг неё надо описать квадрат. Но как? с помощью циркуля и линейки

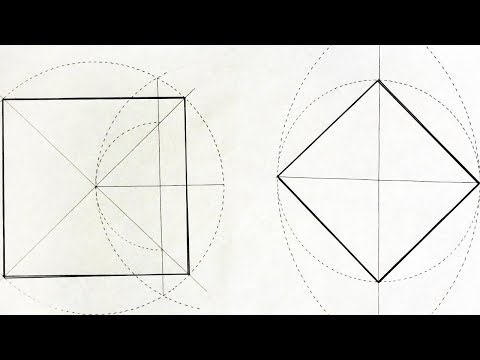
Через центро окружности проводим прямую. На точках пересечения этой прямой и окружности отмечаем точки (назову их А и В) . Проводим 2 окружности, радиусы которых равны и (чуть) больше радиуса этой окружности. Через точки пересечения радиусов проводим прямую (построили перпендикуляр через центр точно) . Там, где этот перпендикуляр пересекает окружность, данную изначально, отмечаем точки (назову их С и D). Соединяем точки (А, С, В, D) и получится четырехугольник (ACBD или ADBC, как точки поставите. ) .
.

Радиус окружности будет равен половине стороны квадрата. Центр — это точка пересечения диагоналей квадрата

Чтобы стороны четырехугольника соприкасались с окружностью. С помощью циркуля рисуешь окружность, а с помощью линейки квадрат. Вроде всё понятно написано.

Я бы так сделала.
Проводим диаметр. Наша задача построить перпендикуляры к диаметру из его крайних точек. Делаем это при помощи циркуля ( сначала насечки справа-слева) , потом из насечек еще по- бол диаметром насечки, соединяем . Длина =R Всего D