При изучении дисциплины «Начертательная геометрия и инженерная графика» студенты должны усвоить правила и последовательность выполнения геометрических построений и сопряжений.
В этом отношении лучшим способом приобретения навыков построения являются задания по вычерчиванию контуров сложных деталей.
Прежде чем приступить к выполнению контрольного задания, нужно изучить технику выполнения геометрических построений и сопряжений по методическому пособию.
- 1. Деление отрезков и углов
- 1.1. Деление отрезка пополам
- 1.2. Деление отрезка на n равных частей
- 1.3. Деление угла пополам
- 2. Деление окружности на равные части и построение правильных многоугольников
- 2.1. Деление окружности на три равные части
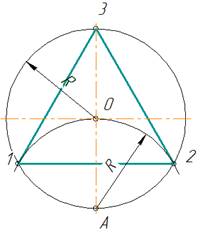
- 2.2. Деление окружности на шесть равных частей
- 2.3. Деление окружности на пять равных частей
- 2.4. Деление окружности на семь равных частей
- Литература
- Обучение школьников делению отрезка, угла и окружности на равные части на уроке черчения
- Аннотация
- Ключевые слова
- Текст научной работы
- Читайте также
- Психолого-педагогическая характеристика детей младшего школьного возраста
- Основные подходы к изучению темы «Базы данных» в школьном курсе информатики
- Развивающие задачи на уроках математики и во внеурочной деятельности
- Организация практической работы № 3 «Моделирование по чертежу» на первом году обучения школьников черчению
- Интегрированное обучение школьников изобразительному искусству и черчению с приобщением их к народному празднику «Масленица» на уроках-экскурсиях
- Список литературы
- Цитировать
- Поделиться
- План открытого урока Геометрические построения. Деление отрезка, окружности на равные части
- 🎥 Видео
Видео:Деление отрезка на равные части, перпендикуляр к прямой.Урок 4.(Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

1. Деление отрезков и углов
Видео:Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

1.1. Деление отрезка пополам
Разделить заданный отрезок АВ пополам.
Примечание. Все необходимые построения должны и могут выполняться только с помощью циркуля и линейки (без делений).
Видео:Инженерная графика. Деление отрезков, углов, окружностей на равные частиСкачать

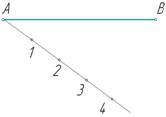
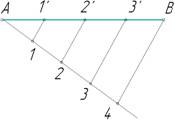
1.2. Деление отрезка на n равных частей
Разделить заданный отрезок на n равных частей.
Из конца отрезка – точки А проведем вспомогательный луч под произвольным углом α.(рис.2 а) На этом луче отложим 4 равных отрезка произвольной длины (рис.2б). Конец последнего, четвертого, отрезка (точку 4) соединим с точкой В. Далее из всех предыдущих точек 1…3 проведем отрезки, параллельные отрезку В4 до пересечения с отрезком АВ в точках1′, 2′, 3′. Полученные таким образом точки разделили отрезок на равные четыре отрезка
Видео:Деление окружностей на равные частиСкачать
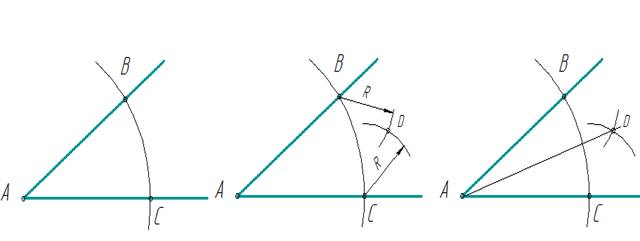
1.3. Деление угла пополам
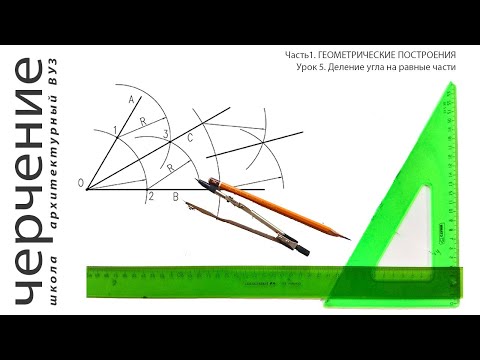
Разделить заданный угол ВАС пополам.
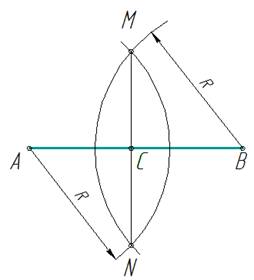
Из вершины угла А произвольным радиусом проводим дугу до пересечения со сторонами угла в точках В и С (рис.3 а). Затем из точек В и С проводим две дуги радиусом, большим половины расстояния ВС, до их пересечения в точке D (рис.3 б). Соединив точки А и D прямой, получаем биссектрису угла, которая делит заданный угол пополам (рис.3 в)
Видео:Деление угла на равные части. Урок 5. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать
2. Деление окружности на равные части и построение правильных многоугольников
Видео:ДЕЛЕНИЕ ОТРЕЗКА НА РАВНЫЕ ЧАСТИ 396 Атанасян 8 классСкачать
2.1. Деление окружности на три равные части
Из конца диаметра, например, точки А (рис.4) проводят дугу радиусом R, равным радиусу заданной окружности. Получают первое и второе деление – точки 1 и 2. Третье деление точка 3, находится на противоположном конце того же диаметра. Соединив точки 1,2,3 хордами, получают правильный вписанный треугольник.
Видео:ДЕЛЕНИЕ ОТРЕЗКА НА РАВНЫЕ ЧАСТИСкачать

2.2. Деление окружности на шесть равных частей
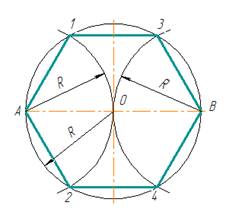
Из концов какого-либо диаметра, например АВ (рис.5), описывают дуги радиусом R окружности. Точки А, 1,3,В,4,2 делят окружность на шесть равных частей. Соединив их хордами, получают правильный вписанный шестиугольник.
Примечание. Вспомогательные дуги проводить полностью не следует, достаточно сделать засечки на окружности.
Видео:Деление окружности на 3 частиСкачать

2.3. Деление окружности на пять равных частей
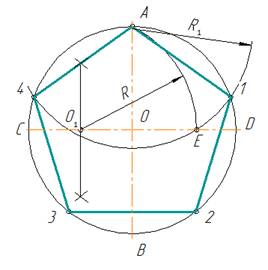
- Проводят два взаимно перпендикулярных диаметра АВ и CD (рис.6). Радиус ОС в точке О1делят пополам.
- Из точки О1, как из центра, проводят дугу радиусом О1А до пересечения ее с диаметром CD в точке Е.
- Отрезок АЕ равен стороне правильного вписанного пятиугольника, а отрезок ОЕ – стороне правильного вписанного десятиугольника.
- Приняв точку А за центр, дугой радиуса R1 = АЕ на окружности отмечают точки 1 и 4. Из точек 1 и 4, как из центров, дугами того же радиуса R1 отмечают точки 3 и 2. Точки А, 1, 2, 3, 4 делятокружность на пять равных частей.
Видео:Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

2.4. Деление окружности на семь равных частей
Из конца диаметра, например, точки А проводят дугу радиуса R, равного радиусу окружности (рис.7). Хорда CD равна стороне правильного вписанного треугольника. Половина хорды CD с достаточным приближением равняется стороне правильного вписанного семиугольника, т.е. делит окружность на семь равных частей.
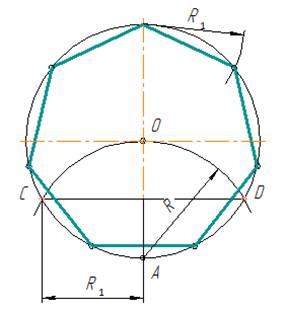
Рис. 7
Видео:Деление окружности на равные части с помощью циркуляСкачать

Литература
- Боголюбов С.К. Инженерная графика: Учебник для средних специальных учебных заведений. – 3-е изд., испр. И доп. — М.: Машиностроение, 2006. – с.392: ил.
- Куприков М.Ю. Инженерная графика: учебник для ССУЗов – М.: Дрофа, 2010 – 495 с.: ил.
- Федоренко В.А., Шошин А.И. Справочник по машиностроительному черчению Л.: Машиностроение. 1976. 336 с.
Copyright © 2010—2022
ООО «Современные медиа технологии в образовании и культуре»
Поддержка
(495) 589-87-71
Сервис «Комментарии» — это возможность для всех наших читателей дополнить опубликованный на сайте материал фактами или выразить свое мнение по затрагиваемой материалом теме.
Редакция Информио.ру оставляет за собой право удалить комментарий пользователя без предупреждения и объяснения причин. Однако этого, скорее всего, не произойдет, если Вы будете придерживаться следующих правил:
- Не стоит размещать бессодержательные сообщения, не несущие смысловой нагрузки.
- Не разрешается публикация комментариев, написанных полностью или частично в режиме Caps Lock (Заглавными буквами). Запрещается использование нецензурных выражений и ругательств, способных оскорбить честь и достоинство, а также национальные и религиозные чувства людей (на любом языке, в любой кодировке, в любой части сообщения — заголовке, тексте, подписи и пр.)
- Запрещается пропаганда употребления наркотиков и спиртных напитков. Например, обсуждать преимущества употребления того или иного вида наркотиков; утверждать, что они якобы безвредны для здоровья.
- Запрещается обсуждать способы изготовления, а также места и способы распространения наркотиков, оружия и взрывчатых веществ.
- Запрещается размещение сообщений, направленных на разжигание социальной, национальной, половой и религиозной ненависти и нетерпимости в любых формах.
- Запрещается размещение сообщений, прямо либо косвенно призывающих к нарушению законодательства РФ. Например: не платить налоги, не служить в армии, саботировать работу городских служб и т.д.
- Запрещается использование в качестве аватара фотографии эротического характера, изображения с зарегистрированным товарным знаком и фотоснимки с узнаваемым изображением известных людей. Редакция оставляет за собой право удалять аватары без предупреждения и объяснения причин.
- Запрещается публикация комментариев, содержащих личные оскорбления собеседника по форуму, комментатора, чье мнение приводится в статье, а также журналиста.
Претензии к качеству материалов, заголовкам, работе журналистов и СМИ в целом присылайте на адрес
Информация доступна только для зарегистрированных пользователей.
Уважаемые коллеги. Убедительная просьба быть внимательнее при оформлении заявки. На основании заполненной формы оформляется электронное свидетельство. В случае неверно указанных данных организация ответственности не несёт.
Видео:Деление отрезка на равные части. Теорема Фалеса. ЧерчениеСкачать

Обучение школьников делению отрезка, угла и окружности на равные части на уроке черчения
Северный (Арктический) федеральный университет им. М.В. Ломоносова, Архангельск
NovaInfo43, с. 296-314
Опубликовано 11 апреля 2016
Раздел: Педагогические науки
Просмотров за месяц: 27
CC BY-NC
Видео:Построение угла, равного данному. 7 класс.Скачать

Аннотация
В статье представлен пример разработки плана-конспекта двадцать пятого урока черчения в школе по теме «Геометрические построения: деление отрезка, угла, и окружности на равные части» для работы с учащимися, изучающими черчение первый год по программе двухгодичной их графической подготовки с использованием пособий учебно-методического комплекта А.Д. Ботвинникова и его соавторов в соответствии с тематическим планированием уроков черчения, разработанным автором данной статьи.
Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Ключевые слова
Видео:Теорема Фалеса Деление отрезка на заданном отношениеСкачать

Текст научной работы
Представленный ниже возможный вариант плана-конспекта урока № 25 для первого года графической подготовки школьников разработан в соответствии с опубликованными нами ранее тематическими планированиями уроков черчения [7 — 8]. При этом были использованы классические пособия учебно-методического комплекта (УМК) по черчению: программа, учебник, рабочая тетрадь, методическое пособие для учителя А.Д. Ботвинникова и его соавторов [1 — 6], а также другая учебно-методическая литература [9 — 23].
Теоретическая основа планирования учебной работы по черчению и подготовки учителя к уроку в развёрнутой форме нами была представлена в отдельной публикации [10]. Были даны образцы планов-конспектов уроков черчения №№ 1 — 6, 14 для первого года графической подготовки школьников [11 — 17]. В отдельном журнале также представлен пример плана-конспекта урока № 5 для второго года обучения школьников черчению с примером анализа предполагаемого или проведённого урока [18].
В учебнике черчения А.Д. Ботвинникова и др. вопросы деления отрезка и угла на равные части его авторами не рассмотрены, ссылаясь на то, что учащиеся эти построения изучали ранее на уроках геометрии и других предметов [2, с. 98-99]. В учебнике рассмотрены лишь деление окружности на равные части и сопряжения. Но мы в предлагаемом ниже плане-конспекте решили представить не только методику обучения школьников делению окружности на равные части, но и дать методику обучения учащихся способам деления отрезка и угла на равные части с использованием классического учебника С.К. Боголюбова [19], поскольку опыт работы в школе показал, что учащиеся зачастую не помнят, как выполнять эти геометрические построения.
План-конспект урока черчения № 25 (Первый год обучения)
Тема урока: Геометрические построения: деление отрезка, угла и окружности на равные части.
Цели урока
- Обучение школьников делению отрезка, угла и окружности на равные части с помощью чертёжных инструментов;
- Закрепить полученные знания школьников путём выполнения ими графический упражнений;
- Дальнейшее формирование умений и навыков работы школьников с чертёжными инструментами, учебными и справочными материалами в процессе их графической деятельности.
- Формировать познавательный интерес учащихся к предмету;
- Содействовать воспитанию терпения, аккуратности, внимания, усидчивости, трудолюбия учащихся, необходимых им для качественного выполнения чертежей;
- Формировать навыки самостоятельной работы школьников во время выполнения ими упражнений;
- Способствовать эстетическому воспитанию школьников путём их обучения красивому расположению изображений на листе бумаги.
- Способствовать дальнейшему развитию глазомера, зрительной памяти и технической речи учащихся.
Учебные пособия, чертежные инструменты, принадлежности и материалы
Для учителя — учебник [2]; учебные таблицы и видеоматериалы, иллюстрирующие деление отрезка, угла и окружности на равные части; образец выполненной графической работы школьником по делению окружности на равные части на уроке вслед за учителем, показывающим построения на классной доске; набор дифференцированных карточек-заданий и варианты их решений; чертежные инструменты и мел для работы на доске.
Для учащихся — учебник [2], ученическая тетрадь, Рабочая тетрадь [3] чертежный лист формата А4 с рамкой и основной надписью, чертёжные инструменты и принадлежности.
Тип урока
Урок изучения нового материала.
Ход урока
1. Организационная часть — 2 мин.
- Приветствие;
- Выявление или назначение дежурных. Напоминание дежурным об их обязанностях;
- Проверка явки учащихся;
- Заполнение учителем классного журнала (можно в конце урока);
- Проверка готовности учащихся к уроку. Выдача учащимся недостающих учебных пособий, чертежных инструментов, принадлежностей и материалов из фонда кабинета для работы на данном занятии.
2. Сообщение темы, цели и задач урока; мотивация учебной деятельности школьников — 3 мин.
2.1. В левой верхней части классной доски учитель мелом заранее пишет чертёжным шрифтом дату проведения урока и его порядковый № 25. В средней верхней части доски указывает тему урока «Геометрические построения: деление отрезка, угла, и окружности на равные части». В правом верхнем углу доски указывает домашнее задание: Повторить § 15.2; тем, кто не успел выполнить классную работу и графическое задание на уроке, дочертить их дома и сдать работы учителю на проверку на следующем уроке.
Обращая внимание учащихся на доску, учитель вслух проговаривает написанное и просит учеников записать полученную информацию в ученических тетрадях.
2.2. Далее учитель ставит перед школьниками цели и задачи урока:
- Научиться правильному делению отрезка, угла и окружности на равные части с помощью чертёжных инструментов;
- Закрепить полученные знания на данном уроке путём выполнения графического упражнения;
- Продолжить: 1) формирование умений и навыков работы с чертёжными инструментами, учебными и справочными материалами в процессе графической деятельности; 2) развитие глазомера, зрительной памяти и технической речи.
2.3. Мотивируя учебную деятельность школьников, учитель сообщает, что материалы данного урока им пригодятся во взрослой жизни при работе, связанной с чертёжно-графической документацией, например, в конструкторских бюро и цехах на машиностроительных заводах и т.д., а в школе — при дальнейшем изучении черчения, в частности, при выполнении различных графических изображений на чертёжных листах, в ученических и Рабочих тетрадях. Кроме того, полученные знания и умения на данном уроке многим из них пригодятся на занятиях по инженерной графике в технических учебных заведениях, куда они могут поступить на дальнейшую учёбу после окончания общеобразовательного учреждения.
Для большей наглядности в процессе мотивации учебной деятельности школьников учителю необходимо продемонстрировать им фотографии технических деталей и их чертежи, выполненные с использованием деления отрезка, угла и окружности на равные части (рис. 1-4; 6-10). Кроме того, демонстрируя рис. 1, школьникам учитель сообщает, что изучаемые на данном уроке геометрические построения широко используются не только при выполнении чертежей и рисунков технических деталей, но и изделий художественно-прикладного искусства с узорами, орнаментами на кружевах, вышивкой, резьбой по дереву и металлу и т.п., продуктов графического дизайна (логотипы, товарные знаки, различные символы), в архитектуре и т.д. [21, с. 30].
В качестве дополнительной мотивации учебной деятельности школьников учитель также сообщает им о том, что графические работы, выполненные ими на этом уроке, будут оценены, а оценки — выставлены в журнал.
Рисунок 1. Примеры использования простейших геометрических построений в технике, дизайне, прикладном искусстве [20, с. 29, рис. 2.31; 21, с. 30, рис. 2.28]
3. Объяснение нового материала — 20 мин.
3.1. Демонстрируя рис. 2 на большом экране, учитель с помощью чертёжных инструментов последовательно показывает школьникам на классной доске деление отрезка прямой на две и четыре равные части. При этом он им сообщает, что из концов отрезка AB циркулем проводят две дуги окружности радиусом R, несколько большим половины данного отрезка, до взаимного пересечения в точках n и m (рис. 2, а). Точки m и n соединяют прямой, которая пересекает отрезок AB в точке C. Точка C делит отрезок AB на две равные части. Проделав подобное построение для отрезка AC, находим его середину — точку D. Повторив построение для отрезка CB, разделим отрезок AB на четыре равные части [19, с. 27]. Школьники вслед за учителем выполняют эти и последующие геометрические построения в своих ученических тетрадях.
Учащимся сообщается, что при вычерчивании детали, показанной на рис. 2, б, применяется способ деления отрезка на четыре части.
Рисунок 2. Деление отрезка прямой на две и четыре равные части: а — деление отрезка на две равные части; б — чертёж детали, выполненный с применением способа деления отрезка на четыре равные части [19, с. 27, рис. 43]
Рисунок 3. Деление отрезка на любое число равных частей с помощью угольника и линейки: а — деление отрезка на одиннадцать равных частей; б — чертёж детали c десятью отверстиями, выполненный с применением способа деления отрезка L на девять равных частей [19, с. 28, рис. 44]
3.2. Деление отрезка прямой на любое число равных частей. Учитель на экран проецирует изображения, представленные на рис. 3. Затем он на классной доске с помощью инструментов показывает способ деления отрезка AB на 11 равных частей. Школьники узнают, что для этого из любого конца данного отрезка, например, из точки B (рис. 3, а), проводят под произвольным острым углом вспомогательную прямую линию BC, на которой от точки B измерительным циркулем откладывают 11 равных отрезков произвольной величины. Крайнюю точку 11 последней отложенной части соединяют с точкой A прямой AB. Затем с помощью линейки и угольника проводят ряд прямых, параллельных прямой 11A, которые и разделяют отрезок AB на 11 равных частей.
На рис. 3, б показана деталь, при изготовлении которой необходимо разместить 10 центров отверстий; отверстия равномерно расположены на длине L. В этом случае применяется описанный выше способ деления отрезка прямой на равные части [19, с. 27-28].
3.3. Учитель обращает внимание школьников на рис. 4, затем начинает объяснять и показывать на классной доске способы деления угла на две и четыре равные части. Так же, как и в предыдущих случаях, каждый школьник выполняет очередные геометрические построения в своей тетради вслед за учителем, объясняющим учебный материал. Используя рис. 4, а и слушая объяснение учителя, школьники в тетради из вершины угла проводят произвольным радиусом дугу до пересечения со сторонами угла BAC в точках n и k. Из полученных точек проводят две дуги радиусом R, несколько большим половины длины дуги nk, до взаимного пересечения в точке m. Вершину угла соединяют с точкой m прямой, которая делит угол BAC пополам. Эта прямая называется биссектрисой угла BAC. Повторяя это построение с полученными углами BAm и mAC угол BAC можно разделить на четыре равные части и т. д. [19, с. 29].
Рисунок 4. Деление углов на равные части: а — деление угла на две и четыре равные части; б — деление прямого угла на три равные части [19, с. 29, рис. 47]
3.4. Изучая способ деления прямого угла на три равные части, школьники из вершины А прямого угла (рис. 4, б) произвольным радиусом R описывают дугу окружности до пересечения ее со сторонами прямого угла в точках a и b, из которых проводят дуги окружности того же радиуса R до пересечения с дугой ab в точках m и n. Точки m и n соединяют с вершиной угла A прямыми и получают стороны Am и An углов BAm и nAC, равных 1 /3 прямого угла, т. е. 30°. Школьникам учитель сообщает, что если каждый из этих углов разделить пополам, то прямой угол будет разделен на шесть равных частей, каждый из углов будет равняться 15°. Прямой угол ABC можно разделить на три равные части угольником с углами 30 и 60° [19, с. 29, рис. 48, а]. При выполнении чертежей нередко требуется разделить прямой угол на две равные части. Это можно выполнять угольником с углом 45° [19, с. 29, рис. 48, б].
Рисунок 5. Образец графической работы школьника по делению окружностей на равные части, выполненной им в ходе изучения темы урока с использованием учебника черчения А.Д. Ботвинникова и др. [2, с. 100 — 102, рис. 124 — 129]
3.5. На данном этапе урока учитель начинает обучать учащихся делению окружности на равные части. С этой целью им предлагается найти рис. 124 — 129 на с. 100 — 102 традиционного школьного учебника «Черчение» [2], рассмотреть их и опираясь на учебную таблицу «Образец графической работы школьников по делению окружностей на равные части» (рис. 5), композиционно правильно наметить центры и начертить циркулем восемь окружностей Ø 40 мм сплошной тонкой линией на чертёжном листе бумаги формата А4 или в ученической тетради. Затем вслед за учителем, объясняющим и показывающим деление окружности на равные части на классной доске с помощью чертёжных инструментов, ребята начинают выполнять геометрические построения — делить окружности на равные части так, как показано на рис. 5.
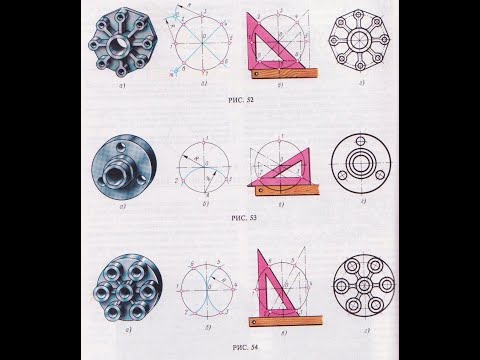
3.5.1. В верхней части листа бумаги (рис. 5) школьники показывают деление окружности на четыре и восемь равных частей с использованием рис.6. На рис.6, а показана крышка, в которой имеется восемь отверстий, равномерно расположенных по окружности. При построении чертежа контура крышки (рис. 6, г) учащимся необходимо разделить окружность на восемь равных частей. Это им можно сделать с помощью угольника с углами 45° (рис. 6, в), гипотенуза угольника должна проходить через центр окружности, или построением.
Рисунок 6. Фото технической детали «Крышка» с восемью равномерно расположенными отверстиями по окружности (а); деление окружности на 4 и 8 равных частей с помощью циркуля (б), угольника и линейки (в); чертёж контура крышки (г) [19, с. 32, рис. 52]
В процессе изучения учебного материала, учащиеся также узнают, что два взаимно перпендикулярных диаметра окружности делят ее на четыре равные части (точки 1, 3, 5, 7 на рис. 6, б). Далее учитель ребятам объясняет, чтобы разделить окружность на восемь равных частей, применяют известный прием деления прямого угла с помощью циркуля на две равные части. Получают точки 2, 4, 6, 8 на рис. 6, б [19, с.31-32].
3.5.2. Деление окружности на три, шесть и двенадцать равных частей учащиеся размещают в средней части и в левом нижнем углу листа бумаги формата А4 (рис. 5). Во фланце (рис. 7, а) имеется три отверстия, равномерно расположенных по окружности. При выполнении чертежа контура фланца (рис. 7, г) нужно разделить окружность на три равные части.
Рисунок 7. Фото технической детали «Фланец» с тремя равномерно расположенными отверстиями по окружности (а); деление окружности на три равные части с помощью циркуля (б), угольника и линейки (в); чертёж контура фланца (г) [19, с. 32, рис. 53]
Учитель ребятам объясняет, что для нахождения точек, делящих окружность радиуса R на три равные части, достаточно из любой точки окружности, например, точки A, провести дугу радиусом R. Пересечения дуги с окружностью дают две искомые точки 2 и 3; третья точка деления будет находиться на пересечении оси окружности, проведенной из точки A, с окружностью (рис. 7, б).
Школьникам сообщается, что разделить окружность на три равные части можно также угольником с углами 30 и 60° (рис. 7, в), гипотенуза угольника должна проходить через центр окружности [19, с. 31 — 32, 34].
Школьники на уроке узнают, что на рис. 8, б показано деление окружности циркулем на шесть равных частей. В этом случае выполняется то же построение, что на рис. 7, б, но дугу описывают не один, а два раза, из точек 1 и 4 радиусом R, равным радиусу окружности.
Рисунок 8. Фото технической детали «Крышка» с шестью равномерно расположенными отверстиями по окружности (а); деление окружности на шесть равных частей с помощью циркуля (б), угольника и линейки (в); чертёж контура крышки (г) [19, с. 32, 34, рис. 54]
Учащиеся убеждаются в том, что разделить окружность на шесть равных частей можно и угольником с углами 30 и 60° (рис. 8, в). На рис. 8, а показана крышка, при выполнении чертежа которой необходимо выполнить деление окружности на шесть частей.
Чтобы выполнить чертеж детали (рис. 9, а), которая имеет 12 отверстий, равномерно расположенных по окружностям, нужно разделить осевую окружность на 12 равных частей (рис. 9, г) [19, с. 31 — 32, 34].
Рисунок 9. Фото технической детали с двенадцатью равномерно расположенными отверстиями по окружности (а); деление окружности на двенадцать равных частей с помощью циркуля (б), угольника и линейки (в); чертёж контура детали (г) [19, с. 32, рис. 55]
Ребята сами догадываются о том, что при делении окружности на 12 равных частей с помощью циркуля можно использовать тот же прием, что и при делении окружности на шесть равных частей (рис. 8, б), но дуги радиусом R описывать четыре раза из точек 1,7, 4 и 10 (рис. 9, б).
Ребята познают, что, используя угольник с углами 30 и 60° с последующим поворотом его на 180°, делят окружность на 12 равных частей (рис. 9, в) [19, с. 31 — 32, 34].
3.5.3. В правом нижнем углу чертёжного листа формата А4 (рис. 5) школьники на уроке показывают деление окружности на пять равных частей вслед за учителем, объясняющим и показывающим графические операции с помощью чертёжных инструментов на классной доске. В плашке (рис. 10, а) имеется пять отверстий, равномерно расположенных по окружности. Выполняя чертеж плашки (рис. 10, в), необходимо разделить окружность на пять равных частей. Через намеченный центр O (рис. 10, б) при помощи рейсшины и угольника проводят осевые линии и из точки O циркулем описывают окружность заданного диаметра. Из точки A радиусом R, равным радиусу данной окружности, проводят дугу, которая пересечет окружность в точке n. Из точки n опускают перпендикуляр на горизонтальную осевую линию, получают точку C. Из точки C радиусом R1, равным расстоянию от точки C до точки 1, проводят дугу, которая пересечет горизонтальную осевую линию в точке m. Из точки 1 радиусом R2, равным расстоянию от точки 1 до точки m, проводят дугу, пересекающую окружность в точке 2. Дуга 12 является 1 /5 длины окружности. Точки 3, 4 и 5 находят, откладывая циркулем отрезки, равные m1.
Рисунок 10. Фото технической детали «Плашка» с пятью равномерно расположенными отверстиями по окружности (а); деление окружности на пять равных частей с помощью циркуля (б); чертёж контура плашки (в) [19, с. 33, рис. 56]
Здесь важно обратить внимание школьников ещё на один способ деления окружности на пять равных частей (рис. 5, нижнее правое изображение). Кроме того, школьникам необходимо предложить найти рис. 129 на с. 102 в учебнике черчения [2]. Авторы учебника пишут, что пятой части окружности соответствует центральный угол в 72° (360°:5=72°). Этот угол можно построить при помощи транспортира. Полученную при этом хорду окружности откладывают раствором циркуля по длине заданной окружности так, как показано на рис. 5 в нижнем правом углу и на рис. 129 (с. 102) в учебнике.
4. Обобщение и закрепление знаний; выполнение графического задания — 15 мин.
4.1. С целью закрепления изученного материала учитель предлагает школьникам устно ответить на следующие вопросы:
- При помощи каких чертёжных инструментов следует делить окружности на равные части? (При помощи линейки, угольников с различными углами, циркуля и транспортира).
- Какой угол делят на три равные части с помощью циркуля? (Прямой угол);
- Чему равен раствор циркуля при делении окружности на три равные части и на шесть равных частей? (Радиусу заданной окружности).
4.2. На втором этапе закрепления изученного материала школьникам предлагается выполнить одно задание из трёх предложенных учителем заданий (рис. 11; 13; 15, а). Предполагаемые образцы выполненных заданий школьниками даны на рис. 12; 14; 15, б).
5. Задание на дом — 1 мин.
Повторить § 15.2. Тем, кто не успел выполнить классную работу и графическое задание на уроке, дочертить их дома и сдать работы учителю на проверку на следующем уроке.
Рисунок 11. Карточка — задание № 1 на выполнение чертежа детали «Пластина» с применением способа деления отрезка на четыре равные части
Рисунок 12. Предполагаемый образец выполненного задания № 1 школьником (к рис. 11)
Рисунок 13. Карточка-задание № 2 на выполнение чертежа детали «Прокладка» с применением способов деления угла пополам и прямого угла на три равные части
Рисунок 14. Предполагаемый образец выполненного задания № 2 школьником (к рис. 13)
Рисунок 15. а — карточка-задание № 3 на выполнение чертежа контура детали с применением деления окружности на четыре равные части; б — предполагаемый образец выполненного задания № 3 школьником (к рис. 15, а)
6. Подведение итогов урока — 4 мин.:
- учитель просит назвать школьников сложности, с которыми они встретились на уроке, затем дает общую характеристику их учебной деятельности на уроке; при этом сообщает им о достижении целей урока, выявленных недостатках и путях их устранения;
- объективно оценивает результаты коллективного и индивидуального труда; выставляет отметки в классный журнал и в дневники учащихся;
- предлагает тем, кто не успел закончить работу на уроке, доделать её дома и принести на следующий урок;
- напоминает дежурным об их обязанностях: после звонка с урока остаться и прибраться в классе, оказать учителю другую необходимую помощь;
- благодарит учащихся за учебно-познавательную деятельность и заканчивает урок.
Видео:Построение 8 угольника циркулемСкачать

Читайте также
Психолого-педагогическая характеристика детей младшего школьного возраста
- Элибаева Л.С.
NovaInfo60, с.309-315, 19 февраля 2017 , Педагогические науки, CC BY-NC
Основные подходы к изучению темы «Базы данных» в школьном курсе информатики
- Векслер В.А.
NovaInfo59, с.293-297, 9 февраля 2017 , Педагогические науки, CC BY-NC
Развивающие задачи на уроках математики и во внеурочной деятельности
- Суханов С.П.
- Воистинова Г.Х.
NovaInfo58, с.395-399, 18 января 2017 , Педагогические науки, CC BY-NC
Организация практической работы № 3 «Моделирование по чертежу» на первом году обучения школьников черчению
- Михайлов Н.Г.
NovaInfo44, с.241-256, 19 апреля 2016 , Педагогические науки, CC BY-NC
Интегрированное обучение школьников изобразительному искусству и черчению с приобщением их к народному празднику «Масленица» на уроках-экскурсиях
- Михайлов Н.Г.
NovaInfo42, с.228-242, 28 марта 2016 , Педагогические науки, CC BY-NC
Видео:1 2 2 деление окружности на 5 равных частейСкачать

Список литературы
- Черчение, 7 — 8 классы (авторы: А.Д. Ботвинников, И.С. Вышнепольский, В.А. Гервер, М.М. Селиверстов: отв. ред. В.А. Гервер) // Программы общеобразовательных учреждений по черчению: Сборник программ / Составители: В.В. Степакова и Л.Е. Самовольнова. – М.: Просвещение, 2000. – 76 с. — С.51 — 60.
- Ботвинников, А.Д. Черчение: 9-й класс: учебник для общеобразовательных учреждений / А. Д. Ботвинников, В.Н. Виноградов, И.С. Вышнепольский. – 4-е изд., дораб. — М.: АСТ: Астрель, 2014. – 221, [3] с.: ил.
- Вышнепольский, В.И. Рабочая тетрадь: К учебнику «Черчение. 9 класс» А.Д. Ботвинникова, В.Н. Виноградова, И.С. Вышнепольского: 9 класс / В.И. Вышнепольский. – М.: АСТ: Астрель, 2014. — 79, [1] с.: ил.
- Ботвинников А.Д. Методическое пособие по черчению: К учебнику А.Д. Ботвинникова и др. «Черчение». 7 – 8 классы» / А.Д. Ботвинников, В.Н.Виноградов, И.С.Вышнепольский и др. – М.: ООО «Издательство Астрель»: ООО «Издательство АСТ», 2003. – 159, [1] с.: ил.
- Виноградов В.Н. Тематическое и поурочное планирование по черчению: К учебнику А.Д. Ботвинникова, В.Н. Виноградова, И.С. Вышнепольского «Черчение»: для 7 – 8 кл.: метод пособие / В.Н. Виноградов. – М.: ЭКЗАМЕН, 2006. – 159, [1] с. – (Учебно-методический комплект).
- Василенко Е.А., Жукова Е.Т. Карточки-задания по черчению для 6 класса: Пособие для учителя. – М.: Просвещение, 1998. – 208 с.: ил.
- Михайлов Н.Г. Тематическое планирование уроков черчения: метод. пособие для учителей / Н.Г. Михайлов; Поморский гос. ун-т им. М.В. Ломоносова. – 3-е изд., перераб. и доп. – Архангельск: Поморский университет, 2009. – 32 с.
- Михайлов Н.Г. Уроки первого года обучения школьников черчению: тематический план к программе и учебнику А.Д. Ботвинникова и др. // Приоритетные научные направления: от теории к практике. — 2014. – № 13. – С. 35 – 43.
- Михайлов Н.Г. Уроки второго года обучения школьников черчению: тематический план к программе и учебнику А.Д. Ботвинникова и др. // Достижения вузовской науки. — 2014. – № 12. – С. 35 — 41.
- Михайлов Н.Г. Методические рекомендации к планированию учебных занятий по черчению в школе // Современная система образования: опыт прошлого – взгляд в будущее. — 2014. — № 3. – С. 140 – 146.
- Михайлов Н.Г. Планирование вводного урока черчения на первом году графической подготовки школьников // Новое слово в науке и практике: гипотезы и апробация результатов исследований. — 2014. – № 13. – С. 33 – 43.
- Михайлов Н.Г. Черчение в школе: План-конспект урока «Понятие о ГОСТ ЕСКД. Форматы, рамка и основная надпись чертежа. Линии чертежа» // Проблемы и перспективы развития образования в России. — 2014. – № 30. – С. 48 – 56.
- Михайлов Н.Г. Черчение в школе: план-конспект урока «Сведения о чертёжном шрифте. Буквы, цифры и знаки на чертежах» // Новый взгляд. Международный научный вестник. — 2014. – № 5. – С. 70 – 80.
- Михайлов Н.Г. Организация графической работы № 1 «Линии чертежа» на первом году обучения школьников черчению // Наука и современность – 2014. – 2014. — № 33. – С. 80 – 86.
- Михайлов Н.Г. Планирование урока черчения на тему «Основные сведения о нанесении размеров. Применение и обозначение масштаба» на первом году графической подготовки школьников // Новое слово в науке и практике: гипотезы и апробация результатов исследований. – 2014. — № 14. – С. 69 – 79.
- Михайлов Н.Г. Организация графической работы № 2 «Чертёж «плоской» детали» на первом году обучения школьников черчению // Психология и педагогика: методика и проблемы практического применения. – 2015. — № 44. – С. 165 – 173.
- Михайлов Н.Г. Обучение школьников теме «Аксонометрические проекции окружностей и предметов с цилиндрическими элементами» на уроке черчения // Психология и педагогика: методика и проблемы практического применения. — 2014. – № 40. – С. 80 – 103.
- Михайлов Н.Г., Емелов К.П. Черчение в школе: План-конспект урока «Понятие о разрезе, сходство и разница между разрезом и сечением, простые разрезы» // Фундаментальные и прикладные исследования: проблемы и результаты. — 2014. – № 14. – С. 29 – 43.
- Боголюбов С.К. Черчение: Учебник для средних специальных учебных заведений. – 2-е изд., испр. – М.: Машиностроение, 1989. – 336 с.: ил.
- Павлова А.А., Жуков С.В. Черчение. Учеб. для уч-ся 9 кл. общеобразоват. учреждений. – М.: Гкманит. Изд. Центр ВЛАДОС, 2003. – 272 с.
- Павлова А.А. Технология. Черчение и графика. 8 – 9 классы: учеб. для общеобразоват. учреждений / А.А. Павлова, Е.И. Корзинова. – 2-е изд., стер. – М.: Мнемозина, 2009. – 263 с.: ил.
- Ерохина Г.Г. Универсальные поурочные разработки по черчению: 9 класс. – М.: ВАКО, 2011. – 160 с. – (В помощь школьному учителю).
- Чепаев Д.И. Домашняя работа по черчению за 7-8 классы к учебнику А.Д. Ботвинникова «Черчение. Учеб. для 7-8 кл. общеобразоват. учреждений». – Учебно-методическое пособие / И.Д.Чепаев. – М.: Издательство «Экзамен», 2005. – 96 с. — (Серия «Решебник»).
Видео:Деление окружности на 12 равных частейСкачать

Цитировать
Михайлов, Н.Г. Обучение школьников делению отрезка, угла и окружности на равные части на уроке черчения / Н.Г. Михайлов. — Текст : электронный // NovaInfo, 2016. — № 43. — С. 296-314. — URL: https://novainfo.ru/article/5108 (дата обращения: 06.02.2022).
Видео:Деление окружности на 3, 4, 5, 6 и 7 равных частейСкачать

Поделиться
Электронное периодическое издание зарегистрировано в Федеральной службе по надзору в сфере связи, информационных технологий и массовых коммуникаций (Роскомнадзор), свидетельство о регистрации СМИ — ЭЛ № ФС77-41429 от 23.07.2010 г.
Соучредители СМИ: Долганов А.А., Майоров Е.В.
Видео:Как разделить угол на равные части с помощью циркуляСкачать

План открытого урока Геометрические построения. Деление отрезка, окружности на равные части
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
УПРАВЛЕНИЕ ОБРАЗОВАНИЯ И НАУКИ ЛИПЕЦКОЙ ОБЛАСТИ
ГОБПОУ «Липецкий машиностроительный колледж»
Зам. директор колледжа по УР
ПЛАН ОТКРЫТОГО ЗАНЯТИЯ
Предмет: инженерная графика
Тема: Геометрические построения.
Деление отрезков, углов, окружностей
на равные части.
Рассмотрен на заседании цикловой комиссии ОТД
Протокол №_______ от ____________________________
Председатель ЦК ОТД: ___________ И.А. Чернова
Составил преподаватель: __________ Е.А. Челокьян
г. Липецк, 2017 год
Технологическая карта занятия
Тема раздела рабочей программы
Геометрические построения. Деление отрезков, углов, окружностей на равные части
Студенты группы АТ-16-1
изучение нового материала
Технология поэтапного формирования умственных действий;
отношение к обучающимся – технология сотрудничества;
по категории обучающихся – технология компенсирующего обучения (педагогической коррекции, выравнивания);
по направлению модернизации обучения – педагогическая технология на основе активизации и интенсификации деятельности обучающихся,
технология здоровьесберегающей организации учебного процесса .
— создать условия для активизации практической деятельности, расширения и закрепления знаний студентов по теме «Геометрические построения»;
— организовать проверку знаний, умений и навыков студентов, полученных в ходе изучения темы;
— обучать навыкам использования конструкторской документации по разработке технологических процессов;
— содействовать воспитанию самостоятельности, ответственности при выполнении задания;
— воспитывать аккуратность при выполнении чертежей и способность проявлять самостоятельность и уверенность при выполнении графической работы.
Формирование общих компетенций:
— Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
— Работать в коллективе и команде, обеспечивать её сплочение, эффективно обращаться с коллегами, руководством, потребителями.
— Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации
— способствовать развитию технического, пространственного и логического мышления;
Формирование общих компетенций:
— Организовывать собственную деятельность, определять методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
— Решать проблемы, оценивать риски и принимать решения в нестандартных ситуациях.
— Осуществлять поиск, анализ и оценку информации, необходимой для постановки и решения профессиональных задач, профессионального и личностного развития.
— Использовать информационно-коммуникативные технологии для совершенствования профессиональной деятельности
Обеспечение учебного занятия
мультимедийное оборудование; персональный компьютер;
— презентации к учебному занятию;
— карточки-задания для учащихся
Урок: Геометрические построения. Деление отрезков, углов, окружностей на равные части
— постановка цели урока и мотивация учебной деятельности;
— воспроизведение и коррекция опорных знаний;
— изложение нового материала;
— подведение итогов урока;
— репродуктивный (индивидуальная практическая работа).
— материалы и изделия;
— особенности проектирования в автомобиле и тракторостроении;
— организация и контроль работ по эксплуатации автомобилей и тракторов.
Формы организации учебной деятельности: фронтальная, индивидуальная.
1. Организационный момент.
2. Приветствует учащихся, наблюдает за готовностью к уроку каждого обучающегося
— Здравствуйте. Записываем тему нашего занятия: «Геометрические построения. Деление отрезков, углов, окружностей на равные части», а я проверю отсутствующих.
3. Постановка цели и задач урока, повторение правил и выработка практических навыков в делении отрезков и окружностей на равные части.
Ставится цель и задачи перед обучающимися: повторить, закрепить и углубить знания о выполнении геометрических построений.
Некоторые детали машин и приборов имеют элементы, равномерно расположенные по окружности, например, такие детали как: крышка, фланец, плашка, звездочка, шкив и др. При выполнении чертежей подобных деталей необходимо знать правила деления окружности на равное количество частей.
На сегодняшнем занятии из многочисленных построений, которые встречаются при выполнении чертежей, мы рассмотрим самые распространенные.
5. Повторение и п роверка знаний:
— Давайте с Вами вспомним, что мы узнали на прошлых занятиях.
Вопрос 1. Какой линией мы чертим основную рамку, надпись и видимый контур детали?
Ответ – Сплошная толстая основная
Вопрос 2. А какая толщина у этой линии?
Вопрос 3. Какой линией мы чертим осевые и центровые?
Ответ – Штрихпунктирная тонкая
Вопрос 4. Какая толщина этой линии?
Вопрос 5. Какой номер шрифта мы применяем на чертеже, когда ставим размеры?
Вопрос 6. Скажите уклон шрифта?
Вопрос 7 . В каких единицах измерения проставляют размеры на чертеже?
6. Изучение нового материала.
При выполнении чертежей деталей приходится делить на равные части отрезки прямой линии, углы, окружности и их дуги. Рассмотрим, как это сделать. (Приложение 1 – Презентация)
Сейчас берем линейку и карандаш и делим свою тетрадь по схеме, которую я вам начерчу на доске (рис.1)

В верхней части листа слева начертите отрезок 50мм. Мы разделим его на 2 и 4 равные части с помощью геометрических построений (рис. 2).

Чтобы разделить отрезок прямой пополам, из его концов проводим дуги радиусом больше половины длины этого отрезка. Точки пересечения дуг соединяем прямой линией, которая делит отрезок прямой на две равные части (АВ=ВБ) и является перпендикуляром к нему.
На четыре равные части отрезок прямой можно разделить аналогично: вначале делим отрезок АБ пополам, а затем каждую половину АВ и ВБ – еще раз пополам, где радиус больше половины этих отрезков.
Так можно делить на любое число равных частей, кратное четырем. А как же на 3, 5, 6, 7 …, п частей? Посмотрите на рис.3: отрезок АБ разделен на 9 равных частей.

Выполняется это так:
— проводим луч АВ под произвольным углом к АБ ;
— откладываем на луче АВ от точки А нужное количество ( п ) равных отрезков произвольной длины;
— соединяем последнюю точку п ( 9 ) с точкой Б ;
— из каждой точки на луче АВ ( 1, 2, 3, …, п ) проводим прямые, параллельные отрезку 9Б , и получаем на АБ требуемое количество равных частей.
Необходимо уметь делить окружность на равные части и строить правильные многоугольники. Любой диаметр делит окружность на 2 равные части.
Для нахождения точек, делящих окружность радиуса R на 3 равные части, достаточно из любой точки окружности, например, точки В, провести дугу радиусом R . Пересечения дуги с окружностью дают две искомые точки 2 и 3 ; третья точка деления будет находиться на пересечении оси окружности, проведенной из точки А , с окружностью (рис. 4).

Разделить окружность на 3 части можно также угольником с углами 30° и 60° (рис. 5). Гипотенуза угольника должна проходить через центр окружности.

Чтобы разделить окружность на 4 части применяют прием деления прямого угла с помощью циркуля на две равные части (рис. 6). Из точек пересечения дуги окружности со сторонами угла (точки А и С ) проводим две пересекающиеся дуги радиуса равного радиусу окружности. Точку их пересечения соединяем с вершиной угла D . Угол А D С и дуга АС разделились пополам. Аналогично делим и угол С D В. Соединив последовательно все точки, получим квадрат.

Разделить окружность на 4 части можно с помощью угольника 45° (рис. 7). Гипотенуза угольника должна проходить через центр окружности.

Чтобы разделить окружность на 4 равные части, нужно провести два взаимно перпендикулярных диаметра окружности ( 13, 24 ). Тоже самое можно выполнить с помощью угольника 45°. Гипотенуза угольника должна проходить через точки пересечения центровых линий и окружности (рис. 8).

Деление окружности на 5 равных частей начинаем с проведения из точки А радиусом окружности R дуги, которая пересекает окружность в двух точках (рис. 9). Соединив точки пересечения прямой, при пересечении с горизонтальной осевой линией получаем точку В. Из точки В, радиусом равным отрезку ВС, проводим дугу, которая пересечет горизонтальную осевую линию в точке D . Соединив точки С и D получаем отрезок С D , который и является 1/5 длины окружности. Из тоски С проводим дугу радиусом равным С D и получаем точки 5 и 2. Из полученных точек проводим еще по одной дуге и находим точки 3 и 4 .

На рис.10 показано деление окружности циркулем на 6 равных частей. В этом случае выполняется то же построение, что и при делении окружности на 3 части, но дугу описывают не один, а два раза, из точек 1 и 4 радиусом окружности R .

Разделить окружность на 6 равных частей можно и при помощи угольника с углами 30° и 60° (рис. 11). Гипотенуза угольника должна проходить через центр окружности.

Разделим окружность на 7 равных частей (рис. 12). Из точки А проводим дугу радиусом окружности R , которая пересекает окружность в двух точках. Соединив точки пересечения прямой, при пересечении с горизонтальной осевой линией получаем точку В. Из точки 1 радиусом, равным отрезку СВ , делают по окружности 7 засечек и получают семь искомых точек.

Чтобы разделить окружность на 8 равных частей, достаточно провести две пары диаметров, т.е. объединить оба случая построения квадрата (рис. 13). Это построение два взаимно перпендикулярных диаметра окружности и прием деления прямого угла с помощью циркуля на две равные части.

Деление окружности на 9 равных частей начинаем с проведения из точки А радиусом окружности R дуги (рис. 14). Из точки С построим вторую дугу радиусом равным отрезку С D , которая пересекает горизонтальную ось окружности в точке Е . Соединив точку пересечения двух дуг F и точку Е , получаем отрезок равный 1/9 длины окружности. Из точки 1 радиусом, равным отрезку F Е , делают по окружности 9 засечек и получают девять искомых точек.

Чтобы разделить окружность на 10 равных частей, нужно сначала разделить ее на 5 равных частей (рис. 15). Отрезок Е D является стороной десятиугольника. Из точки 1 радиусом, равным отрезку Е D , делают по окружности 10 засечек и получают десять искомых точек.

При делении окружности на 12 равных частей с помощью циркуля используют тот же прием, что и при делении окружности на 6 равных частей (рис. 16), но дуги радиусом окружности R описывать 4 раза из точек 1, 4, 7 , 10 .

Используя угольник с углами 30° и 60° с последующим поворотом на 180°, делят окружность на 12 равных частей (рис.17).

С достаточной точностью можно делить окружность на число равных частей, пользуясь таблицей коэффициентов для подсчета длины хорды (рис.18).

Зная, на какое число ( п ) следует разделить окружность, находят по таблице коэффициент k . При умножении коэффициента k на диаметр окружности D получают длину хорды l , которую циркулем откладывают на окружности п раз (рис. 19).

7. Подведение итогов урока. Рефлексия.
8. Домашнее задание.
Раздаю карточки на построение деталей с делением окружности на равные части (Приложение 2).
🎥 Видео
Теорма Фалеса или задача о деление отрезка на равные частиСкачать